02 【人教版】九年级上第二次月考数学试卷（含答案解析）(1)

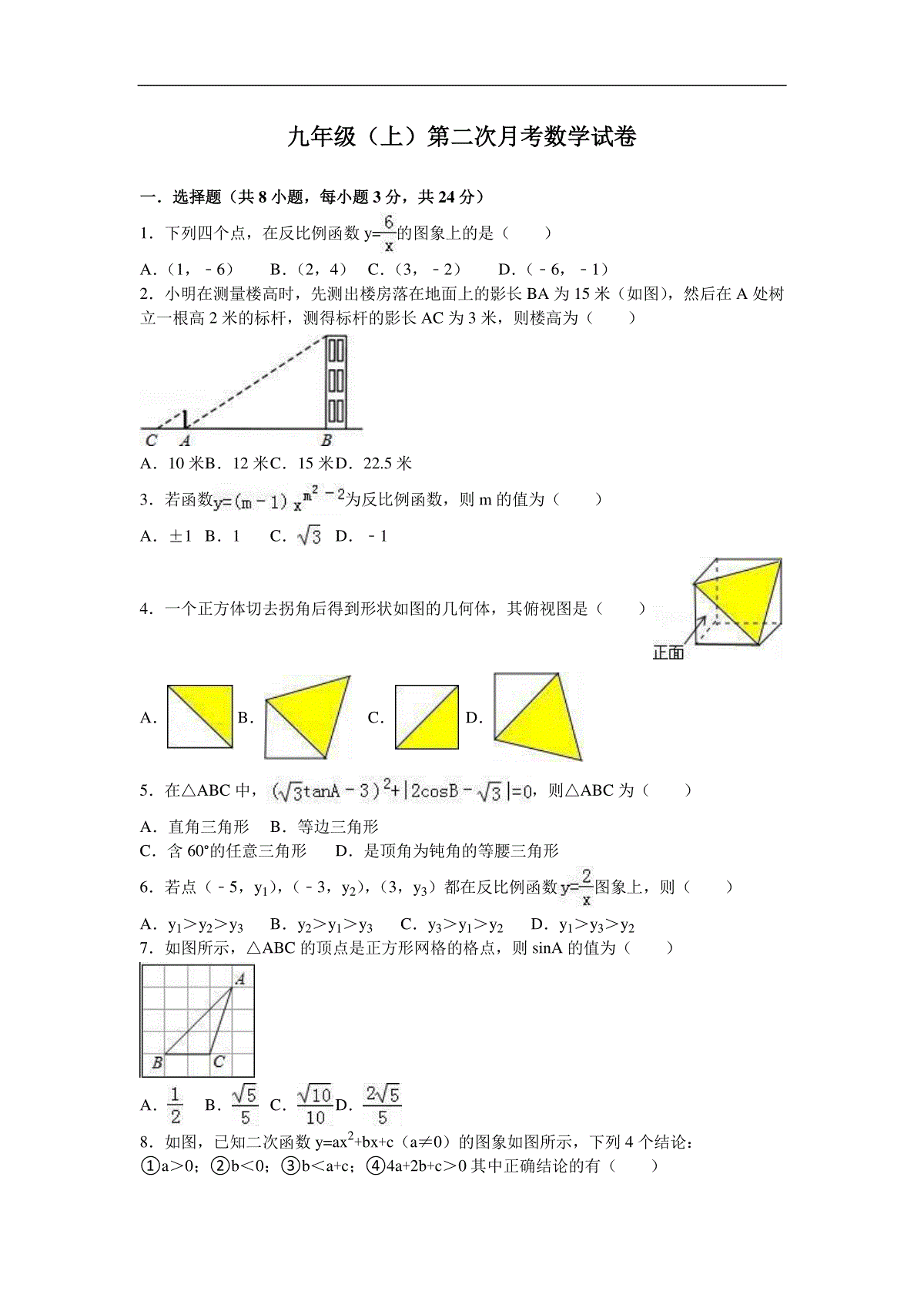
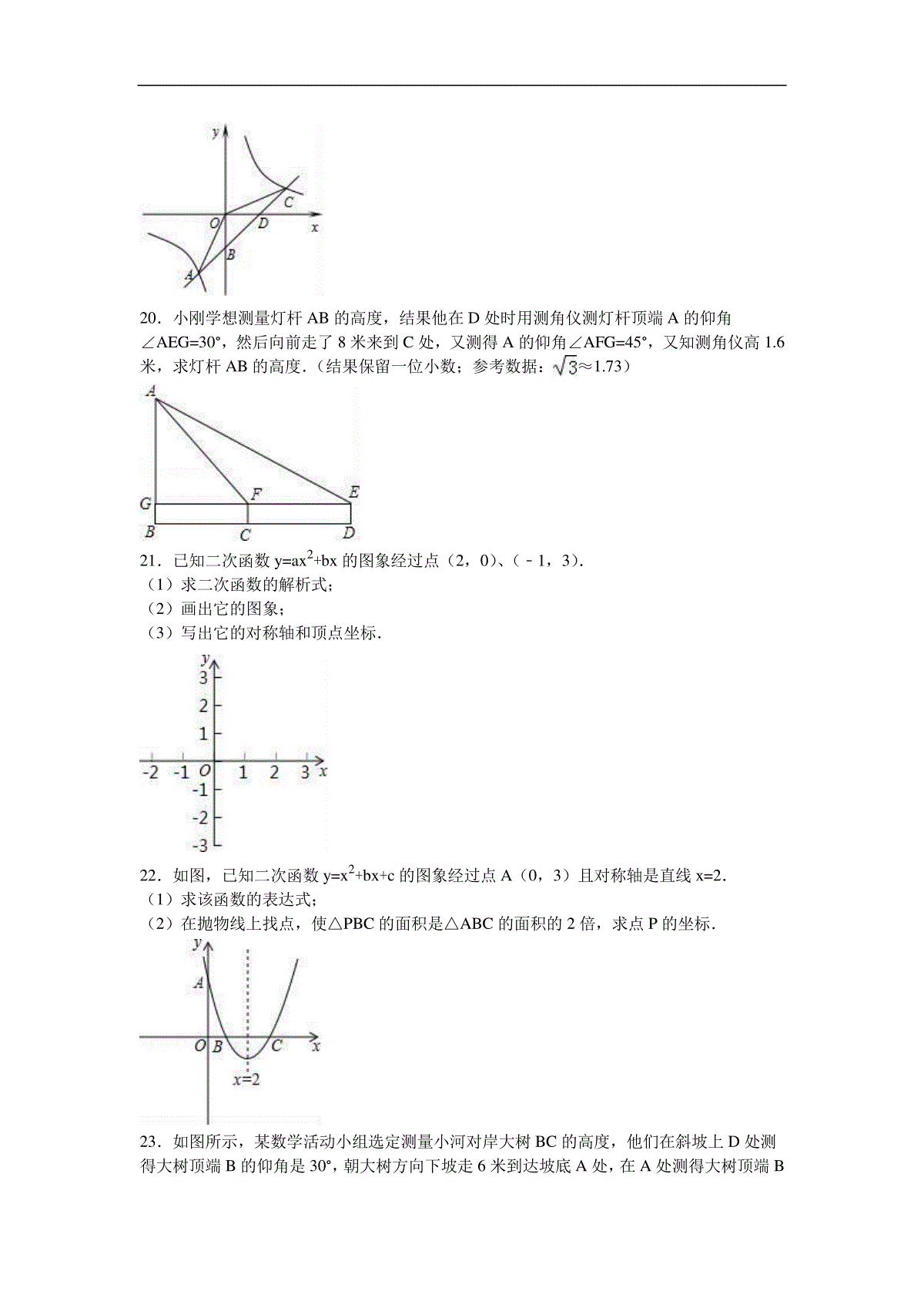
九年级（上）第二次月考数学试卷一．选择题（共8小题，每小题3分，共24分）1．下列四个点，在反比例函数y=的图象上的是（）A．（1，﹣6）B．（2，4）C．（3，﹣2）D．（﹣6，﹣1）2．小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（）A．10米B．12米C．15米D．22.5米3．若函数为反比例函数，则m的值为（）A．±1B．1C．D．﹣14．一个正方体切去拐角后得到形状如图的几何体，其俯视图是（）A．B．C．D．5．在△ABC中，，则△ABC为（）A．直角三角形B．等边三角形C．含60°的任意三角形D．是顶角为钝角的等腰三角形6．若点（﹣5，y1），（﹣3，y2），（3，y3）都在反比例函数图象上，则（）A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y1＞y2D．y1＞y3＞y27．如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（）A．B．C．D．8．如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列4个结论：①a＞0；②b＜0；③b＜a+c；④4a+2b+c＞0其中正确结论的有（）A．①②③B．①②④C．①③④D．②③④二、填空题（共7小题，每小题3分，共21分）9．若α为锐角，tanα•tan30°=1，则α=度．10．如图，一次函数y=mx与反比例函数y=的图象交于A、B两点，过点A作AM⊥x轴，垂足为M，连接BM，若S△ABM=3，则k的值是．11．在我们刚刚学过的九年级数学下册课本第11页，用“描点法”画某个二次函数图象时，列了如下表格：x…345678…y…7.553.533.55…根据表格上的信息回答问题：该二次函数在x=9时，y=．12．用配方法将二次函数y=﹣x2+x﹣1化成y=a（x﹣h）2+k的形式，则y=．13．如图，直线y=kx与双曲线y=（x＞0）交于点A（1，a），则k=．14．如图，在矩形ABCD中，点E在AB边上，沿CE折叠矩形ABCD，使点B落在AD边上的点F处．若AB=4，BC=5，则tan∠AFE的值为．15．如图，已知AB、CD分别表示两幢相距30米的大楼，小明在大楼底部点B处观察，当仰角增大到30度时，恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像，那么大楼AB的高度为米．三、解答题：（共75分16．计算（1）﹣2cos45°+（7﹣）0﹣（）﹣1+tan30°（2）×sin45°﹣（）﹣2+|﹣3|﹣．17．如图，路灯下一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一颗大树，它的影子是MN．（1）指定路灯的位置（用点P表示）；（2）在图中画出表示大树高的线段；（3）若小明的眼睛近似地看成是点D，试画图分析小明能否看见大树．18．已知y=y1﹣y2，y1与x成反比例，y2与（x﹣2）成正比例，并且当x=3时，y=5，当x=1时，y=﹣1；求y与x之间的函数关系式．19．如图，一次函数y=kx+b的图象与反比例函数y=的图象交于点A﹙﹣2，﹣5﹚，C﹙5，n﹚，交y轴于点B，交x轴于点D．（1）求反比例函数y=和一次函数y=kx+b的表达式；（2）连接OA，OC．求△AOC的面积．（3）当kx+b＞时，请写出自变量x的取值范围．20．小刚学想测量灯杆AB的高度，结果他在D处时用测角仪测灯杆顶端A的仰角∠AEG=30°，然后向前走了8米来到C处，又测得A的仰角∠AFG=45°，又知测角仪高1.6米，求灯杆AB的高度．（结果保留一位小数；参考数据：≈1.73）21．已知二次函数y=ax2+bx的图象经过点（2，0）、（﹣1，3）．（1）求二次函数的解析式；（2）画出它的图象；（3）写出它的对称轴和顶点坐标．22．如图，已知二次函数y=x2+bx+c的图象经过点A（0，3）且对称轴是直线x=2．（1）求该函数的表达式；（2）在抛物线上找点，使△PBC的面积是△ABC的面积的2倍，求点P的坐标．23．如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡角∠FAE=30°，求大树的高度（结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，≈1.73）九年级（上）第二次月考数学试卷参考答案与试题解析一．选择题（共8小题，每小题3分，共24分）1．下列四个点，在反比例函数y=的图象上的是（）A．（1，﹣6）B．（2，4）C．（3，﹣2）D．（﹣6，﹣1）【考点】反比例函数图象上点的坐标特征．【分析】根据反比例函数图象上点的坐标特征进行判断．【解答】解：∵1×（﹣6）=﹣6，2×4=8，3×（﹣2）=6，（﹣6）×（﹣1）=6，∴点（3，﹣2）在反比例函数y=的图象上．故选D．2．小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（）A．10米B．12米C．15米D．22.5米【考点】相似三角形的应用．【分析】在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似．根据相似三角形的对应边的比相等，即可求解．【解答】解：∵=即=，∴楼高=10米．故选A．3．若函数为反比例函数，则m的值为（）A．±1B．1C．D．﹣1【考点】反比例函数的定义．【分析】根据反比例函数的定义即可求出m的值．【解答】解：根据题意得：m2﹣2=﹣1，且m﹣1≠0解得：m=﹣1．故选D．4．一个正方体切去拐角后得到形状如图的几何体，其俯视图是（）A．B．C．D．【考点】简单几何体的三视图．【分析】根据俯视图是从上面看到的图形判定则可．【解答】解：从上面看，是正方形右下角有阴影，故选C．5．在△ABC中，，则△ABC为（）A．直角三角形B．等边三角形C．含60°的任意三角形D．是顶角为钝角的等腰三角形【考点】特殊角的三角函数值；非负数的性质：绝对值；非负数的性质：偶次方．【分析】首先结合绝对值以及偶次方的性质得出tanA﹣3=0，2cosB﹣=0，进而利用特殊角的三角函数值得出答案．【解答】解：∵（tanA﹣3）2+|2cosB﹣|=0，∴tanA﹣3=0，2cosB﹣=0，∴tanA=，cosB=，∠A=60°，∠B=30°，∴△ABC为直角三角形．故选：A．6．若点（﹣5，y1），（﹣3，y2），（3，y3）都在反比例函数图象上，则（）A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y1＞y2D．y1＞y3＞y2【考点】反比例函数图象上点的坐标特征．【分析】根据反比例函数图象上点的坐标特征，分别计算出y2、y1、y3的值，然后比较大小即可．【解答】解：当x=﹣5时，y1=﹣；当x=﹣3时，y2=﹣；当x=3时，y3=，所以y2＜y1＜y3．故选C．7．如图所示，△ABC的顶点是正方形网格的格点，则sinA的值为（）A．B．C．D．【考点】锐角三角函数的定义；勾股定理．【分析】利用网格构造直角三角形，根据锐角三角函数的定义解答．【解答】解：如图：在B点正上方找一点D，使BD=BC，连接CD交AB于O，根据网格的特点，CD⊥AB，在Rt△AOC中，CO==；AC==；则sinA===．故选：B．8．如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列4个结论：①a＞0；②b＜0；③b＜a+c；④4a+2b+c＞0其中正确结论的有（）A．①②③B．①②④C．①③④D．②③④【考点】二次函数图象与系数的关系．【分析】①首先根据抛物线开口向上，可得a＞0，故①正确；②然后根据抛物线的对称轴为直线x=﹣＞0，可得b＜0，故②正确；③根据二次函数y=ax2+bx+c（a≠0）的图象，可得当x=﹣1时，y＞0，所以a﹣b+c＞0，故③正确．④根据二次函数y=ax2+bx+c（a≠0）的图象，可得当x=2时，y＜0，所以4a+2b+c＜0，故③不正确；故选A．【解答】解：∵抛物线开口向上，∴a＞0，故①正确；∵抛物线的对称轴为直线x=﹣＞0，∴b＜0，故②正确；∵当x=﹣1时，y＞0，∴a﹣b+c＞0，∴故③正确；∵x=2时，y＜0，∴4a+2b+c＜0，∴结论④错误；综上，可得正确的结论有：①②③．故选A．二、填空题（共7小题，每小题3分，共21分）9．若α为锐角，tanα•tan30°=1，则α=60度．【考点】特殊角的三角函数值．【分析】本题可根据tan30°=，得出tanα的值，再运用三角函数的特殊值解出α的值．【解答】解：∵tan30°=，tanα•tan30°=1，∴tanα=，又∵α为锐角，∴α=60°．故答案为：60．10．如图，一次函数y=mx与反比例函数y=的图象交于A、B两点，过点A作AM⊥x轴，垂足为M，连接BM，若S△ABM=3，则k的值是3．【考点】反比例函数系数k的几何意义；反比例函数图象的对称性．【分析】由反比例函数图象的对称性和反比例函数系数k的几何意义可得：△ABM的面积为△AOM面积的2倍，S△ABM=2S△AOM=|k|．【解答】解：由题意得：S△ABM=2S△AOM=3，S△AOM=|k|=，则k=3．故答案为：3．11．在我们刚刚学过的九年级数学下册课本第11页，用“描点法”画某个二次函数图象时，列了如下表格：x…345678…y…7.553.533.55…根据表格上的信息回答问题：该二次函数在x=9时，y=7.5．【考点】二次函数的图象．【分析】根据二次函数的图象关于对称轴对称并观察表格知当x=3和当x=9时的函数值相等，据此可以求得当x=9时的函数值．【解答】解：∵二次函数的图象关于对称轴对称，且观察表格知低昂x=4和当x=8时的函数值相等，∴当x=3和当x=9时的函数值相等，∵当x=3时y=7.5，∴当x=9时y=7.5．故答案为7.5．12．用配方法将二次函数y=﹣x2+x﹣1化成y=a（x﹣h）2+k的形式，则y=﹣（x﹣1）2﹣．【考点】二次函数的三种形式．【分析】利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．【解答】解：y=﹣x2+x﹣1，=﹣（x2﹣2x+1）﹣1﹣，=﹣（x﹣1）2﹣，即y=﹣（x﹣1）2﹣，故答案是：﹣（x﹣1）2﹣．13．如图，直线y=kx与双曲线y=（x＞0）交于点A（1，a），则k=2．【考点】反比例函数与一次函数的交点问题．【分析】直接利用图象上点的坐标性质进而代入求出即可．【解答】解：∵直线y=kx与双曲线y=（x＞0）交于点A（1，a），∴a=2，k=2，故答案为：2．14．如图，在矩形ABCD中，点E在AB边上，沿CE折叠矩形ABCD，使点B落在AD边上的点F处．若AB=4，BC=5，则tan∠AFE的值为．【考点】翻折变换（折叠问题）．【分析】由四边形ABCD是矩形，可得：∠A=∠B=∠D=90°，CD=AB=4，AD=BC=5，由折叠的性质可得：∠EFC=∠B=90°，CF=BC=5，由同角的余角相等，即可得∠DCF=∠AFE，然后在Rt△DCF中，即可求得答案．【解答】解：∵四边形ABCD是矩形，∴∠A=∠B=∠D=90°，CD=AB=4，AD=BC=5，由题意得：∠EFC=∠B=90°，CF=BC=5，∴∠AFE+∠DFC=90°，∠DFC+∠FCD=90°，∴∠DCF=∠AFE，∵在Rt△DCF中，CF=5，CD=4，∴DF=3，∴tan∠AFE=tan∠DCF==．故答案为：．15．如图，已知AB、CD分别表示两幢相距30米的大楼，小明在大楼底部点B处观察，当仰角增大到30度时，恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像，那么大楼AB的高度为20米．【考点】解直角三角形的应用-仰角俯角问题．【分析】根据仰角为30°，BD=30米，在Rt△BDE中，可求得ED的长度，根据题意恰好能