双馈电机数学建模

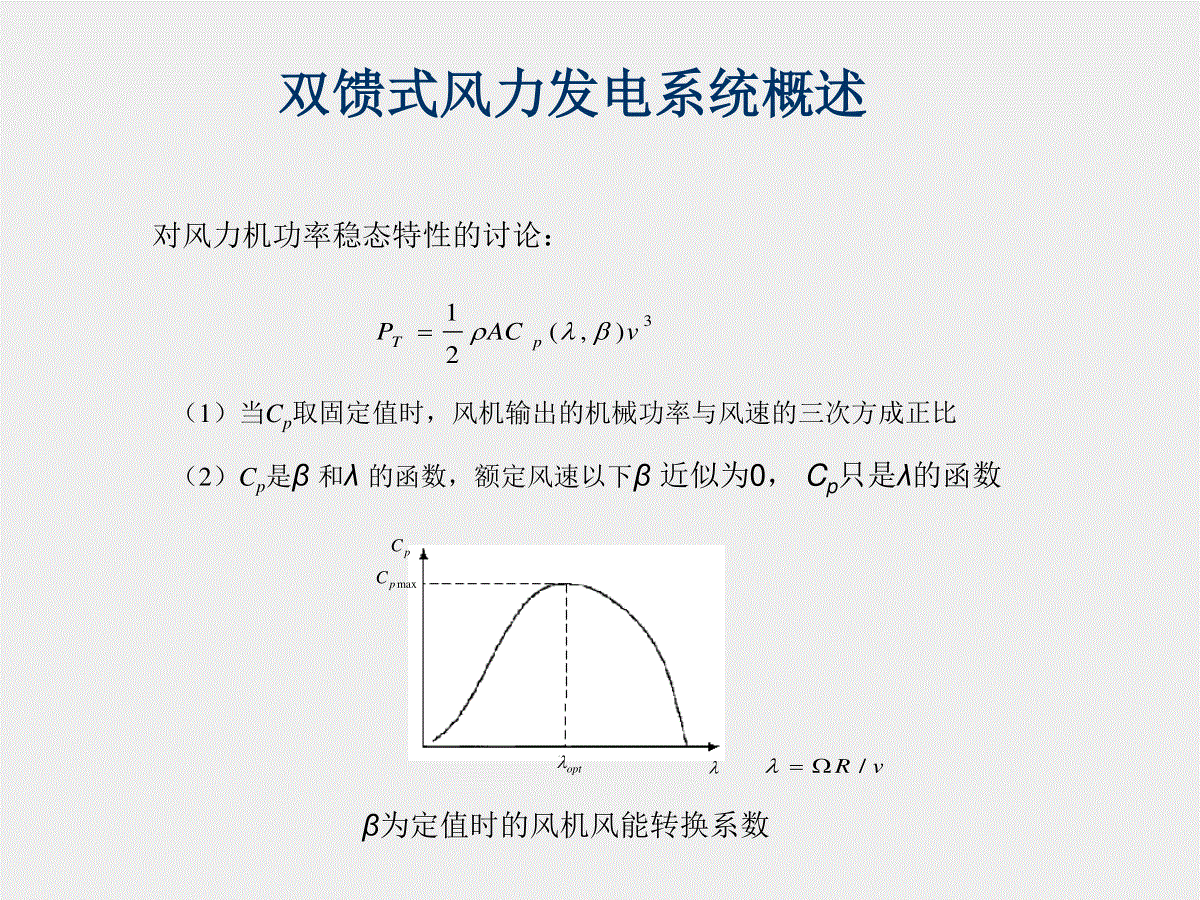
双馈式风力发电系统概述1.风力发电机组控制结构AC/DC电网风力机网侧变流器齿轮箱双馈发电机机侧变流器SPWM调制励磁调节系统直流环节调节系统SPWM调制DC/AC变流器控制系统最大风能捕捉算法及浆距调节双馈风力发电机组由风力机、传动轴及齿轮箱、双馈感应发电机和双PWM变流器及其控制系统组成。（1）风力机作用是通过叶轮捕获风能，将风能转化为轮毂上的机械转矩（2）传动轴及齿轮箱的作用是将风力机的驱动作用传递给发电机并提升转速（3）双馈感应发电机类似于绕线式异步电机，它作用是将机械能转化为电能（4）双PWM变流器由两个用直流联结的背靠背电压源逆变器（VSC）组成，分别为机侧变流器和网侧变流器（5）机侧变流器的基本功能是为双馈发电机提供励磁电压，并且在矢量控制策略下实现有功和无功的解耦调节（6）网侧变流器的主要功能是在直流调节系统的控制下维持电容电压恒定，同时具有调节功率因数的功能。双馈式风力发电系统概述2.最大风能追踪风力机作为风力发电的原动机，是一个复杂的动态元件，尤其是浆距调节系统，涉及到电机驱动、液压系统等元件。但是，如果所研究的问题时间尺度为秒级以下，则考虑浆距调节系统各元件动态行为的意义不大，故仅考虑稳态意义下的功率特性3),(21vACPpT风力机功率稳态特性为：——空气密度A——风轮扫风面积——风能转换系数pC——叶尖速比——风力机转速——叶片半径R——桨距角——风速vvR/2.1风力机功率稳态特性双馈式风力发电系统概述对风力机功率稳态特性的讨论：3),(21vACPpT（1）当Cp取固定值时，风机输出的机械功率与风速的三次方成正比（2）Cp是β和λ的函数，额定风速以下β近似为0，Cp只是λ的函数optpCmaxpCβ为定值时的风机风能转换系数vR/双馈式风力发电系统概述风力机的气动特性（1）对同一转速而言，风机捕获功率随风速增大而增大；（2）对同一风速而言，仅有一个转速点使风机捕获最大功率；（3）浆距角增加时，Cp迅速下降。此特性用于高风速下控制风机转速双馈式风力发电系统概述2.2最大风能追踪（MPPT）原理描述：双馈式风力发电系统概述2.3风力机仿真模型风速立方运算乘法运算2/A风机转速乘R除法除法v3vRpCTP机械转矩3),(21vACPpToptpCmaxpC双馈电机动态数学模型和坐标变换本节提要双馈电机物理结构双馈电机的多变量非线性数学模型坐标变换和变换矩阵双馈电机在两相坐标系上的数学模型双馈电机在两相坐标系上的状态方程1双馈电机的物理结构1双馈电机的物理结构2.1三相异步电动机的物理模型ABCuAuBuC1uaubucabc2双馈电机的多变量非线性数学模型1.电压方程三相定子、转子绕组的电压平衡方程分别为tRiuddAsAAtRiuddBsBBtRiuddCsCCtRiuddaraatRiuddbrbbtRiuddcrcc2.1三相异步电动机的数学模型ABCuAuBuC1uaubucabc电压方程的矩阵形式将电压方程写成矩阵形式，并以微分算子p代替微分符号d/dtcbaCBAcbaCBArrrssscbaCBA000000000000000000000000000000piiiiiiRRRRRRuuuuuu或写成ΨRiup2.磁链方程每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和，因此，六个绕组的磁链可表达为cbaCBAcCcbcacCcBcAbcbbbabCbBbAacabaaaCaBaACcCbCaCCCBCABcBbBaBCBBBAAcAbAaACABAAcbaCBAiiiiiiLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLLL或写成LiΨ将磁链方程写成分块矩阵的形式rsrrrssrssrsiiLLLLΨΨTCBAsΨTcbarΨTiiiCBAsiTiiicbaricos)120cos()120cos()120cos(cos)120cos()120cos()120cos(cosmsLTsrrsLLrsL值得注意的是，和两个分块矩阵互为转置，且均与转子位置有关，它们的元素都是变参数srLABCuAuBuC1uaubucabc2.2坐标变换和变换矩阵对于abc坐标系下异步电机的动态数学模型：ΨRiup求解这组时变微分方程是十分困难的。解决方法是坐标变换。LiΨ坐标变换基本出发点：在不同坐标系下所产生的磁动势完全一致众所周知，交流电机三相对称的静止绕组A、B、C，通以三相平衡的正弦电流时，所产生的合成磁动势是旋转磁动势F，它在空间呈正弦分布，以同步转速1（即电流的角频率）顺着A-B-C的相序旋转。这样的物理模型绘于下图a中。（1）三相绕组产生的旋转磁势ABCABCiAiBiCFω1a）三相交流绕组•旋转磁动势的产生然而，旋转磁动势并不一定非要三相不可，除单相以外，二相、三相、四相、……等任意对称的多相绕组，通以平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。（2）两相交流电机绕组产生的旋转磁势Fiiω1b）两相交流绕组图b中绘出了两相静止绕组和，它们在空间互差90°，通以时间上互差90°的两相平衡交流电流，也产生旋转磁动势F。当图a和b的两个旋转磁动势大小和转速都相等时，即认为图b的两相绕组与图a的三相绕组等效。（3）旋转直流绕组产生的旋转磁势1FMTimitMTc）旋转的直流绕组再看图c中的两个匝数相等且互相垂直的绕组M和T，其中分别通以直流电流im和it，产生合成磁动势F，其位置相对于绕组来说是固定的。如果让包含两个绕组在内的整个铁心以同步转速旋转，则磁动势F自然也随之旋转起来，成为旋转磁动势。把这个旋转磁动势的大小和转速也控制成与图a和图b中的磁动势一样，那么这套旋转的直流绕组也就和前面两套固定的交流绕组都等效了。当观察者也站到铁心上和绕组一起旋转时，在他看来，M和T是两个通以直流而相互垂直的静止绕组。•等效的概念由此可见，以产生同样的旋转磁动势为准则，图a的三相交流绕组、图b的两相交流绕组和图c中整体旋转的直流绕组彼此等效。或者说，在三相坐标系下的iA、iB、iC，在两相坐标系下的i、i和在旋转两相坐标系下的直流im、it是等效的，它们能产生相同的旋转磁动势。现在的问题是，如何求出iA、iB、iC与i、i和im、it之间准确的等效关系，这就是坐标变换的任务。三相--两相变换（3/2变换）现在先考虑上述的第一种坐标变换——在三相静止绕组A、B、C和两相静止绕组、之间的变换，或称三相静止坐标系和两相静止坐标系间的变换，简称3/2变换。下图中绘出了A、B、C和、两个坐标系，为方便起见，取A轴和轴重合。设三相绕组每相有效匝数为N3，两相绕组每相有效匝数为N2，各相磁动势为有效匝数与电流的乘积，其空间矢量均位于有关相的坐标轴上。由于交流磁动势的大小随时间在变化着，图中磁动势矢量的长度是随意的。•三相和两相坐标系与绕组磁动势的空间矢量N2iN3iAN3iCN3iBN2iβ60o60oCB设磁动势波形是正弦分布的，当三相总磁动势与二相总磁动势相等时，两套绕组瞬时磁动势在、轴上的投影都应相等，)2121(60cos60cosCBA3C3B3A3α2iiiNiNiNiNiN)(2360sin60sinCB3C3B3β2iiNiNiNiN写成矩阵形式，得CBA23β2323021211αiiiNNii考虑变换前后总功率不变，在此前提下，可以证明，匝数比应为3223NN令C3/2表示从三相坐标系变换到两相坐标系的变换矩阵，则2323021211322/3C•三相—两相坐标系的变换矩阵如果三相绕组是Y形联结不带零线，则有iA+iB+iC=0，或iC=iAiB。即：BAβ221023αiiiiβBAα2161032iiii按照所采用的条件，电流变换阵也就是电压变换阵，同时还可证明，它们也是磁链的变换阵。两相—两相旋转变换（2s/2r变换）从上图等效的交流电机绕组和直流电机绕组物理模型的图b和图c中从两相静止坐标系到两相旋转坐标系M、T变换称作两相—两相旋转变换，简称2s/2r变换，其中s表示静止，r表示旋转。把两个坐标系画在一起，即得下图。两相静止和旋转坐标系与磁动势（电流）空间矢量itsiniFs1imcosimimsinitcosiβitMT图中，两相交流电流i、i和两个直流电流im、it产生同样的以同步转速1旋转的合成磁动势Fs。由于各绕组匝数都相等，可以消去磁动势中的匝数，直接用电流表示，例如Fs可以直接标成is。但必须注意，这里的电流都是空间矢量，而不是时间相量。M，T轴和矢量Fs（is）都以转速1旋转，分量im、it的长短不变，相当于M，T绕组的直流磁动势。但、轴是静止的，轴与M轴的夹角随时间而变化，因此is在、轴上的分量的长短也随时间变化，相当于绕组交流磁动势的瞬时值。由图可见，i、i和im、it之间存在下列关系sincostmαiiicossintmβiii•2s/2r变换公式写成矩阵形式，得tms2/r2tmβαcossinsincosiiCiiiicossinsincoss2/r2C是两相旋转坐标系变换到两相静止坐标系的变换阵。式中•两相旋转—两相静止坐标系的变换矩阵对上式两边都左乘以变换阵的逆矩阵，即得βαβα1tmcossinsincoscossinsincosiiiiiicossinsincosr2/s2C则两相静止坐标系变换到两相旋转坐标系的变换阵是电压和磁链的旋转变换阵也与电流（磁动势）旋转变换阵相同。•两相静止—两相旋转坐标系的变换矩阵1.异步电机在两相任意旋转坐标系（dq坐标系）上的数学模型两相坐标系可以是静止的，也可以是旋转的，其中以任意转速旋转的坐标系为最一般的情况，有了这种情况下的数学模型，要求出某一具体两相坐标系上的模型就比较容易了。2.3三相异步电机在两相坐标系上的数学模型•变换关系设两相坐标d轴与三相坐标A轴的夹角为s，而ps=dqs为dq坐标系相对于定子的角转速，dqr为dq坐标系相对于转子的角转速。ABCFsdqssdq要把三相静止坐标系上的电压方程、磁链方程和转矩方程都变换到两相旋转坐标系上来，可以先利用3/2变换将方程式中定子和转子的电压、电流、磁链和转矩都变换到两相静止坐标系、上，然后再用旋转变换阵C2s/2r将这些变量变换到两相旋转坐标系dq上。•变换过程具体的变换运算比较复杂，此处从略，需要时可参看相关文献。ABC坐标系坐标系dq坐标系3/2变换C2s/2r（1）磁链方程dq坐标系磁链方程[式（附3-8）]为rqrdsqsdrmrmmsmsrqrdsqsd00000000iiiiLLLLLLLL