控制工程第三章

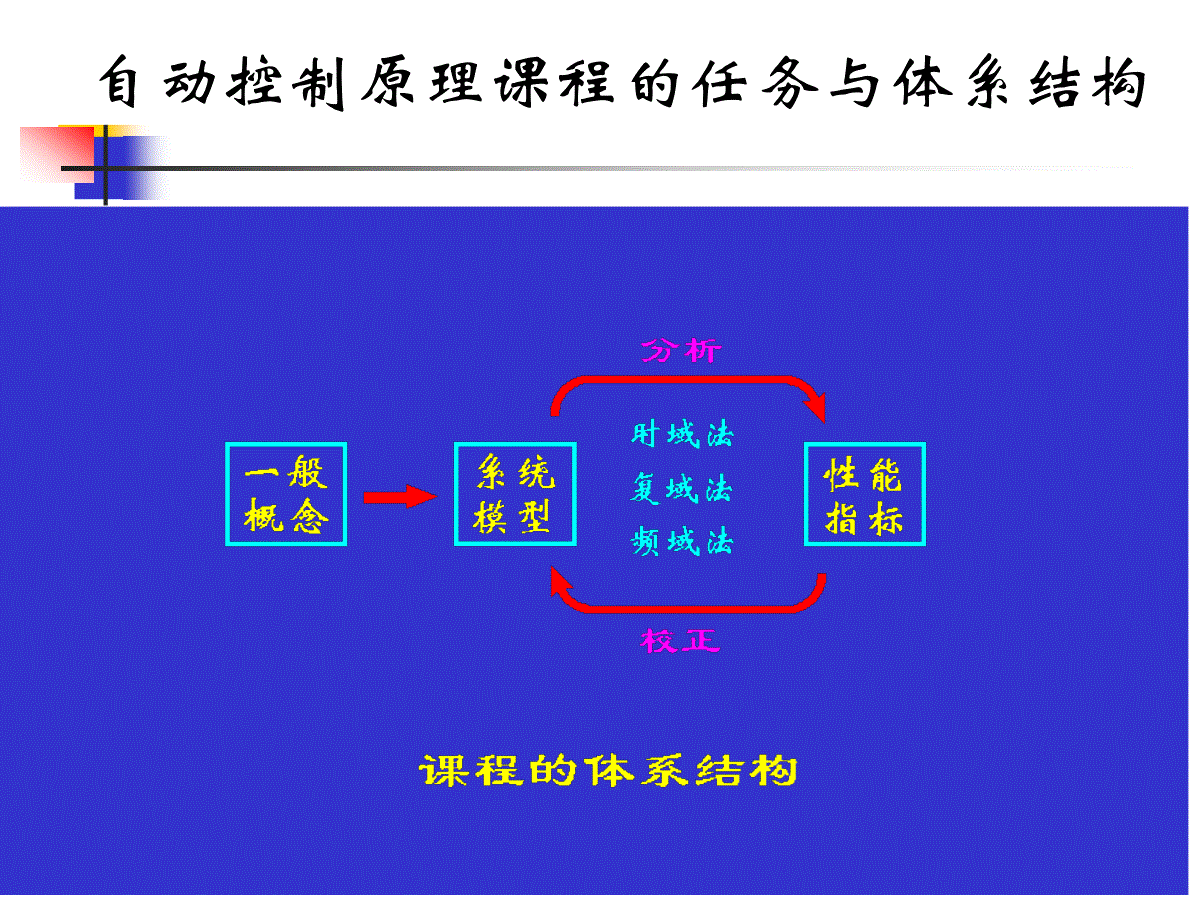
自动控制原理课程的任务与体系结构第三章时间响应分析3.1时间响应及其组成3.3一阶系统3.4二阶系统3.6系统误差分析与计算3.2典型输入信号3.5高阶系统3.7函数在时间响应中的作用线性系统的时域分析(时间响应分析)时域法的作用和特点时域法是最基本的分析方法,学习复域法、频域法的基础(1)直接在时间域中对系统进行分析校正，直观，准确；(2)可以提供系统时间响应的全部信息；(3)基于求解系统输出的解析解，比较烦琐。稳：(基本要求)系统受脉冲扰动后能回到原来的平衡位置准:(稳态要求）稳态输出与理想输出间的误差(稳态误差)要小快:(动态要求)过渡过程要平稳，迅速延迟时间td—阶跃响应第一次达到终值的50％所需的时间上升时间tr—阶跃响应从终值的10％上升到终值的90％所需的时间有振荡时，可定义为从0到第一次达到终值所需的时间峰值时间tp—阶跃响应越过终值达到第一个峰值所需的时间调节时间ts—阶跃响应到达并保持在终值2％误差带内所需的最短时间超调量δ％—峰值超出终值的百分比线性系统时域性能指标超调量σ%=AB100%时间td延迟h(t)t时间tr上升峰值时间tpBAh(t)t动态性能指标定义调节时间ts系统的时间响应分析时间响应及组成常系数线性微分方程的解的特点例1（课本）Collegeofmechanical&electronicengineering第三章时域分析法3.1时间响应及其组成微分方程的解包括两部分：通解（自由响应）和特解（强迫响应）设系统的微分方程为)()()()(0111txtyadttydadttydannnnnn方程的解为：)()()(21tytyty通解自由响应瞬态响应特解强迫响应稳态响应设对应齐次微分方程的特征根Si(i=1、2……n)各不相同，则Collegeofmechanical&electronicengineering第三章时域分析法3.1时间响应及其组成tsniinitsiiieAeAty12111)()()(,)(211tBtyeAtynitsii而y1(t)中包含两部分：由系统的初态引起的自由响应，称为零输入响应由输入引起的自由响应，称为零状态响应)(txCollegeofmechanical&electronicengineering第三章时域分析法3.1时间响应及其组成0ReiS零状态响应自由响应)()(1121tBeAeAtyiisniniitsi强迫响应零输入响应控制工程研究的往往就是系统的零状态响应若，则随着时间的增加，自由响应逐渐衰减，当时，自由响应趋于0，此时系统稳定，故自由响应又称为瞬态响应（暂态响应）。tCollegeofmechanical&electronicengineering第三章时域分析法3.1时间响应及其组成0ReiSSiRet若，则随着时间的增加，自由响应逐渐增大，当时，自由响应也趋于无穷大，此时系统是不稳定的，自由响应不是瞬态响应（暂态响应）。而稳态响应一般就是强迫响应是大于0还是小于0，决定了自由响应是衰减还是发散，决定了系统稳定还是不稳定；而稳定时，的绝对值是大还是小，决定了自由响应是快速衰减还是慢速衰减，决定了系统是快速还是瞒速趋于稳定响应SiReCollegeofmechanical&electronicengineering第三章时域分析法3.1时间响应及其组成iSImmntxbtxbtxbtxbtyadttydadttydammmmnnnnnn),()()()()()()(01)1(1)(0111)(tx在很大程度上决定了自由响应的振荡情况，决定了系统的响应在规定时间内接近稳态响应的情况，影响着响应的准确性，也就是说系统的自由响应反映了系统的“稳、准、快”的性能。若线性定常微分方程的输入函数有导数项，即方程形式为：若输入仅为，对方程求导dttdxdttdyadttydadttydannnnnn)()()()(0111Collegeofmechanical&electronicengineering第三章时域分析法3.1时间响应及其组成)(tx)(ty)(ty)(tx)(ty以作为新的输入函数，则作为新的输出函数也就是说此时所产生的输出为的导数故当以的n阶导数作为输入时，所产生的输出就为的n阶导数从系统的角度来说，对同一线性定常系统，若输入函数等于某函数的导函数，则该输入函数所引起的响应函数也就等于该函数的响应函数的导函数，即：)()()()(tytxtytx典型输入信号在时间域进行分析时，为了比较不同系统的控制性能，需要规定一些具有典型意义的输入信号建立分析比较的基础。这些信号称为控制系统的典型输入信号。第三章时域分析法3.2典型输入信号Collegeofmechanical&electronicengineering通常规定控制系统的初始状态为零状态。即在外作用加于系统之前，被控量及其各阶导数相对于平衡工作点的增量为零，系统处于相对平衡状态。典型初始状态典型输入信号§3.1.2时域法常用的典型输入信号一阶系统一阶系统Ф(s)标准形式及h(s)sKsG)(11111)(1TsTsTKsKsKsKsKTT11TsssTssRssC111111)()()(TtesCLth1)()(1一阶系统动态性能指标tTeth11)(tTeTth11)(Thhh1)0(1)(0)0(98.01)(Ttsseth02.098.01TtseTTts402.0ln一阶系统单位阶跃响应的特点响应分为两部分瞬态响应：Tte表示系统输出量从初态到终态的变化过程（动态/过渡过程）稳态响应：1表示时，系统的输出状态t，随时间的推移，指数增大，且无振荡。，无稳态误差；txo00ox1oxCollegeofmechanical&electronicengineering第三章时域分析法3.3一阶系统，即经过时间T，系统响应达到其稳态输出值的63.2%，从而可以通过实验测量惯性环节的时间常数T；632.011eTxo时间常数T反映了系统响应的快慢。通常工程中当响应曲线达到并保持在稳态值95%~98%时，认为系统响应过程基本结束。从而惯性环节的过渡过程时间为。TT4~3Collegeofmechanical&electronicengineeringTdttdxto1)(0第三章时域分析法3.3一阶系统一阶系统的单位脉冲响应1)(sXiTsTsGsXo111)()(0,1)(teTtxTtoxo(t)1/T0t0.3681T斜率xo(t)T21TCollegeofmechanical&electronicengineering第三章时域分析法3.3一阶系统一阶系统单位脉冲响应的特点xo(0)=1/T,随时间的推移，xo(t)指数衰减；对于实际系统，通常应用具有较小脉冲宽度（脉冲宽度小于0.1T）和有限幅值的脉冲代替理想脉冲信号。201)(Tdttdxto瞬态响应：稳态响应：0TteT1Collegeofmechanical&electronicengineering第三章时域分析法3.3一阶系统例1系统如图所示，现采用负反馈方式，欲将系统调节时间减小到原来的0.1倍，且保证原放大倍数不变，试确定参数Ko和KH的取值。HOHOHOKsKsKsKsGKSGKs1012.01012.010112.010)(1)()(10*1011002.0*1012.0KKKTKHOH109.0OHKK11012.010110sKKKHHO2K例：一阶系统结构图如图3-45所示。要求系统闭环增益，调节时间4.0sts，试确定参数21,KK解由结构图写出闭环系统传递函数111)(212211211KKsKKKsKsKKsKs令闭环增益212KK，得：5.02K令调节时间4.03321KKTts，得：151K。的值。§3.2.3一阶系统的典型响应r(t)R(s)C(s)=s)R(s)c(t)一阶系统典型响应t)11(t)t一阶系统的典型响应asatwLs])([)(ateth1)(atataeethtw]1[)()()(1)()(sGsGs)(])(1)[(sGsGssaasaasasssG1)(1)()(例2已知单位反馈系统的单位阶跃响应试求闭环传函s,单位脉冲响应w(t),开环传函G(s)。解．)()()()(ssGssG)(1)()(sssG二阶系统传递函数标准形式及分类222222121)(nnnssTssTsφ√ξ2-1S1,2=-ξωn±ωnS1,2=-ξωn-ωn=S1,2=±jωn0＜ξ＜1ξ＝1ξ＝0ξ＞1j0j0j0j0二阶系统单位阶跃响应-±j√1-ξ2ωnS1,2=ωnξh(t)=1T2tT1T21e+T1tT2T11e+h(t)=1-(1+ωnt)e-ωtnh(t)=1-cosωntj0j0j0j0T11T21ξ＞1ξ＝10＜ξ＜1ξ＝0sin(ωdt+β)e-ξωth(t)=√1-ξ211n过阻尼临界阻尼欠阻尼零阻尼欠阻尼二阶系统（振荡环节）：01具有一对共轭复数极点：dnnnjjp22,11系统时域响应含有衰减的复指数振荡项：tdjtntdjneee)(其中，称为有阻尼固有频率。21ndCollegeofmechanical&electronicengineering第三章时域分析法3.4二阶系统临界阻尼二阶系统：＝1具有两个相等的负实数极点：np2,1tne系统时域响应含有衰减项：过阻尼二阶系统：1具有两个不相等的负实数极点：系统包含两类瞬态衰减分量：tnn1exp2122,1nnpCollegeofmechanical&electronicengineering第三章时域分析法3.4二阶系统零阻尼二阶系统：＝0具有一对共轭虚极点：njp2,1负阻尼二阶系统：0极点实部大于零，响应发散，系统不稳定。系统时域响应含有复指数振荡项：tnjeCollegeofmechanical&electronicengineering第三章时域分析法3.4二阶系统不同阻尼比下，极点分布的情况减幅振荡等幅振荡无振荡无振荡Collegeofmechanical&electronicengineering第三章时域分析法3.4二阶系统二阶系统的单位阶跃响应ssXi1)()2()()()(222nnniossssXsGsX欠阻尼（01）状态0),sin(11)(2ttetxdtno其中，21ndarccos12arctgCollegeofmechanical&electronicengineering第三章时域分析法3.4二阶系统欠阻尼二阶系统单位阶跃响应的特点瞬态分量为振幅等于的阻尼正弦振荡，其振幅衰减的快慢由和n决定。有阻尼固有频率；21tne21nd振荡频率随减小而加大,增加可以降低振荡，但系统快速性降低。一定时，n越大，瞬态响应分量衰减越迅速，系统响应快速性越好。，无稳态误差；1)(oxCollegeofmechanical&electronicengineering第三章时域分析法3.4二阶系统欠阻尼二阶系统单位阶跃响应