机器学习课程论文

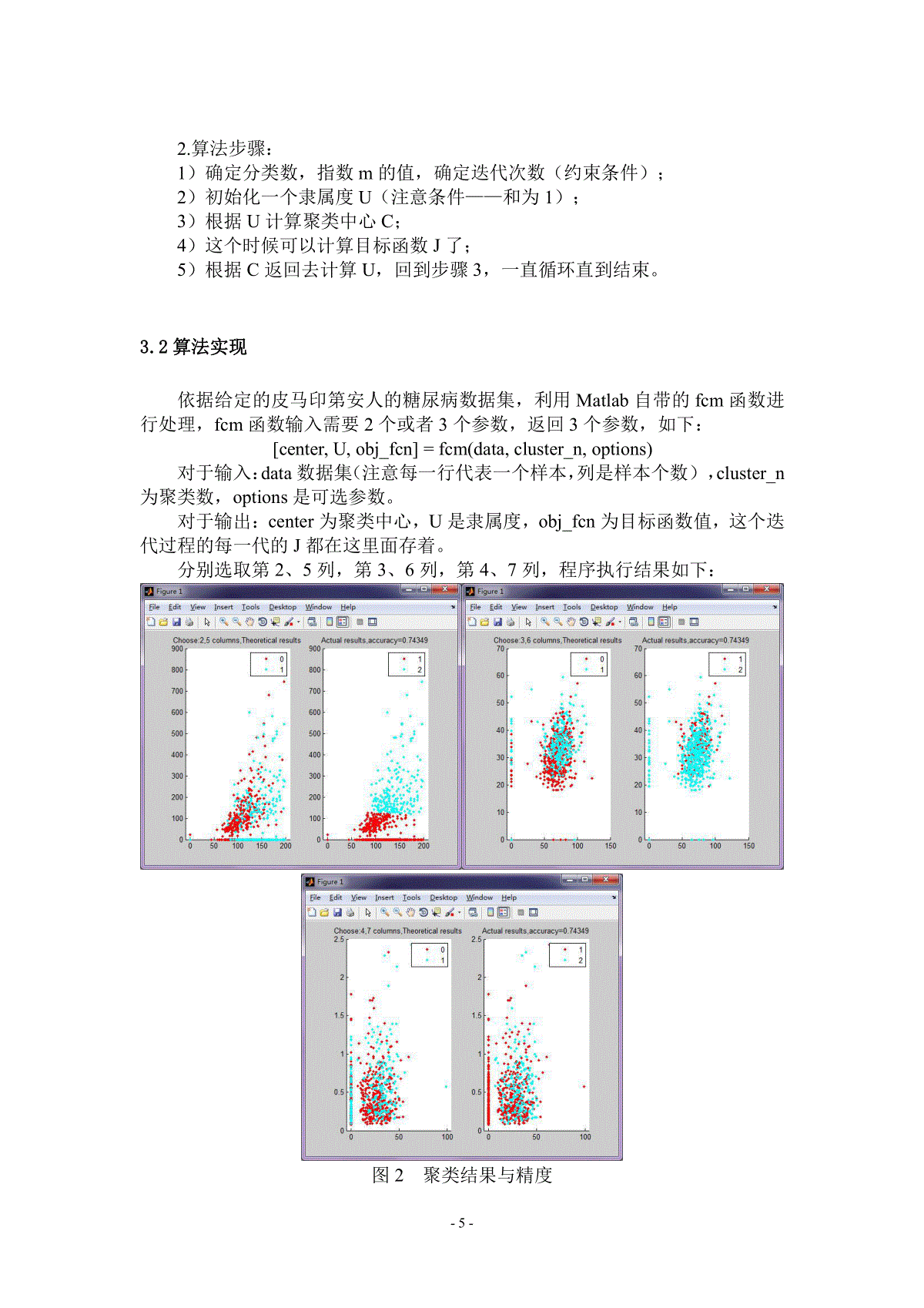
-1-Similarityanddifferencebetweensupervisedlearningandunsupervisedlearning【摘要】本文对机器学习中常见的两类方法——监督学习和无监督学习进行了简单的探讨，以此来加深对机器学习算法的认识和理解。首先，简要阐述了监督学习和无监督学习的定义；然后利用给定的皮马印第安人糖尿病的数据集，分别利用监督学习中的KNN算法和无监督学习中的FCM算法对数据集进行了相应的处理，前者的分类精度最佳（k=7时）为0.7625，后者的聚类准确率达到了0.7435，并探讨了如何评价聚类结果的优劣性；最后，依据上述实验结果，讨论了监督学习和无监督学习的异同点。关键词：机器学习、糖尿病、分类、聚类、多变量1.监督学习和无监督学习机器学习的常用方法，主要分为监督学习(supervisedlearning)和无监督学习(unsupervisedlearning)。首先看，什么是学习（learning）？一个成语就可概括：举一反三。以高考为例，高考的题目在上考场前我们未必做过，但在高中三年我们做过很多很多题目，懂解题方法，因此考场上面对陌生问题也可以算出答案。机器学习的思路也类似：我们能不能利用一些训练数据（已经做过的题），使机器能够利用它们（解题方法）分析未知数据（高考的题目）？最简单也最普遍的一类机器学习算法就是分类（classification）。对于分类，输入的训练数据有特征（feature），有标签（label）。所谓的学习，其本质就是找到特征和标签之间的关系（mapping）。这样当有特征而无标签的未知数据输入时，我们就可以通过已有的关系得到未知数据的标签。在上述的分类过程中，如果所有训练数据都有标签，则称为监督学习（supervisedlearning）。如果数据没有标签，显然就是无监督学习（unsupervisedlearning）了，也即聚类（clustering）。常见的监督学习方法有k近邻法（k-nearestneighbor，KNN）、决策树、朴素贝叶斯法、支持向量机（SVM）、感知机和神经网络等等；无监督学习方法有划分法、层次法、密度算法、图论聚类法、网格算法和模型算法几大类，常见的具体算法有K-means算法、K-medoids算法和模糊聚类法（FCM）。-2-2.监督学习应用举例——KNN算法KNN算法是典型的监督学习方法，是从训练集中找到和新数据最接近的k条记录，然后根据他们的主要分类来决定新数据的类别。该算法涉及3个主要因素：训练集、距离或相似的衡量、k的大小。本文将以KNN算法为例，利用给定的皮马印第安人的糖尿病数据集，来说明监督学习方法的应用。2.1算法要点1.算法思想：基本思想是“近朱者赤、近墨者黑”：给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。2.算法步骤：1）算距离：计算已知类别数据集合汇总的点与当前点的距离，按照距离递增次序排序；2）找邻居：选取与当前点距离最近的k个点；3）做分类：确定距离最近的前k个点所在类别的出现频率，返回距离最近的前k个点中频率最高的类别作为当前点的预测分类。3.算法规则：1）k值设定：k太小，分类结果易受噪声点影响；k太大，近邻中又可能包含太多的其它类别的点。k值通常是采用交叉检验来确定（以k=1为基准）。经验规则：k一般低于训练样本数的平方根。2）距离度量：什么是合适的距离衡量？距离越近应该意味着这两个点属于一个分类的可能性越大。常用的距离衡量包括欧氏距离、夹角余弦等。变量值域对距离的影响：值域越大的变量常常会在距离计算中占据主导作用，因此应先对变量进行标准化。3）分类决策规则：投票决定：少数服从多数，近邻中哪个类别的点最多就分为该类。加权投票法：根据距离的远近，对近邻的投票进行加权，距离越近则权重越大（权重为距离平方的倒数）。投票法没有考虑近邻的距离的远近，距离更近的近邻也许更应该决定最终的分类，所以加权投票法更恰当一些。-3-2.2算法实现利用给定的皮马印第安人的糖尿病数据集，编写matlab程序来实现KNN算法。对新的输入实例，判定其类标的部分代码如下：prediction.mfunctionpredicted_label=prediction(testing_input,data,labels,k)%testing_input为输入测试数据的一行，data为训练样本数据集，labels为训练样本的类标A=bsxfun(@minus,data,testing_input);%训练数据集逐行与输入的测试数据行向量相减distanceMat=sum(A.^2,2);%求测试数据与训练集每一个样本点（即训练集的一行）的欧氏距离[B,IX]=sort(distanceMat,'ascend');%对各个欧氏距离进行排序，B为排序后的列向量，IX为相对位置的索引向量，满足B=distanceMat(IX)len=min(k,length(B)^0.5);%k一般低于训练样本数的平方根predicted_label=mode(labels(IX(1:len)));%出现的频率最高的类标，作为测试数据的类标end在主程序中载入训练数据集和测试数据集，调用prediction.m，依据经验规则，104160k。故k值设定从1开始，依次递增，直到12为止，分类精度与k值设定的结果如下表所示：表1k值设定与分类精度k123456accuracy0.693750.731250.7250.731250.731250.75k789101112accuracy0.76250.73750.743750.73750.718750.7375由表1可知，k值的设定会影响分类预测的精度，这是因为当k太小时，分类结果易受噪声点影响；k太大时，近邻中又可能包含太多的其它类别的点。因此，表中结果展示，分类预测精度随着k值的增大而增大，当k值超过某个值时，分类预测精度反而下降了。故而本例中最佳分类精度时，k值应取7，k=7时的程序执行结果如下图所示：-4-图1k=7时的分类预测精度3.无监督学习应用举例——FCM算法模糊C均值（FuzzyC-means）算法简称FCM算法，是一种基于目标函数的模糊聚类算法，主要用于数据的聚类分析。K-means与FCM都是经典的聚类算法，K-means是排他性聚类算法，即一个数据点只能属于一个类别，而FCM只计算数据点与各个类别的相似度。可理解为：对任一个数据点，使用K-means算法，其属于某个类别的相似度要么100%要么0%（非是即否）；而对于FCM算法，其属于某个类别的相似度只是一个百分比。本文将以FCM算法为例，利用给定的皮马印第安人的糖尿病数据集，来说明无监督学习方法的应用。3.1算法要点FCM算法是基于对目标函数的优化基础上的一种数据聚类方法。聚类结果是每一个数据点对聚类中心的隶属程度，该隶属程度用一个数值来表示。FCM算法是一种无监督的模糊聚类方法，在算法实现过程中不需要人为的干预。1.算法思想：首先介绍一下模糊这个概念，所谓模糊就是不确定，确定性的东西是什么那就是什么，而不确定性的东西就说很像什么。比如说把20岁作为年轻不年轻的标准，那么一个人21岁按照确定性的划分就属于不年轻，而我们印象中的观念是21岁也很年轻，这个时候可以模糊一下，认为21岁有0.9分像年轻，有0.1分像不年轻，这里0.9与0.1不是概率，而是一种相似的程度，把这种一个样本属于结果的这种相似的程度称为样本的隶属度，一般用u表示，表示一个样本相似于不同结果的一个程度指标。基于此，假定数据集为X，如果把这些数据划分成c类的话，那么对应的就有c个类中心为C，每个样本j属于某一类i的隶属度为iju。-5-2.算法步骤：1）确定分类数，指数m的值，确定迭代次数（约束条件）；2）初始化一个隶属度U（注意条件——和为1）；3）根据U计算聚类中心C；4）这个时候可以计算目标函数J了；5）根据C返回去计算U，回到步骤3，一直循环直到结束。3.2算法实现依据给定的皮马印第安人的糖尿病数据集，利用Matlab自带的fcm函数进行处理，fcm函数输入需要2个或者3个参数，返回3个参数，如下：[center,U,obj_fcn]=fcm(data,cluster_n,options)对于输入：data数据集（注意每一行代表一个样本，列是样本个数），cluster_n为聚类数，options是可选参数。对于输出：center为聚类中心，U是隶属度，obj_fcn为目标函数值，这个迭代过程的每一代的J都在这里面存着。分别选取第2、5列，第3、6列，第4、7列，程序执行结果如下：图2聚类结果与精度-6-3.3聚类精度聚类没有统一的评价指标，总体思想为一个cluster聚类内的数据点聚集在一起的密度越高，圈子越小，离center中心点越近，类内越近，类间越远，那么这个聚类的总体质量相对来说就会越好。4.监督学习和无监督学习的异同监督学习最常见的就是分类，通常我们为算法输入大量已分类数据作为算法的训练集，训练集的每一个样本都包含了若干个特征和一个类标，通过已有的训练样本去训练得到一个最优模型，然后利用这个最优模型将所有陌生输入映射为相应的输出，对于输出进行判断实现分类，这就对未知数据进行了分类。与监督学习相对应的是无监督学习，此时数据没有类别信息，也不会给定目标值。在无监督学习中，将数据集合分成由类似的对象组成的多个类的过程被称为聚类，将寻找描述数据统计值的过程称之为密度估计。无监督学习与监督学习的不同之处，主要是它没有训练样本，而是直接对数据进行建模。典型案例就是聚类了，其目的是把相似的东西聚在一起，而不关心这一类是什么。聚类算法通常只需要知道如何计算相似度就可以了，它可能不具有实际意义。5.参考文献[1]李航，《统计学习方法》，清华大学出版社，2012[2]周志华，《机器学习》，清华大学出版社，2016[3]JiaweiHan,MichelineKamber,JianPei著，范明、孟小峰译，《数据挖掘概念与技术（第三版）》，机械工业出版社，2012[4]薛山，《MATLAB基础教程》，清华大学出版社，2011[5]陈杰等，《MATLAB宝典（第3版）》，电子工业出版社，2011[6][7][8]