函数极值说课稿

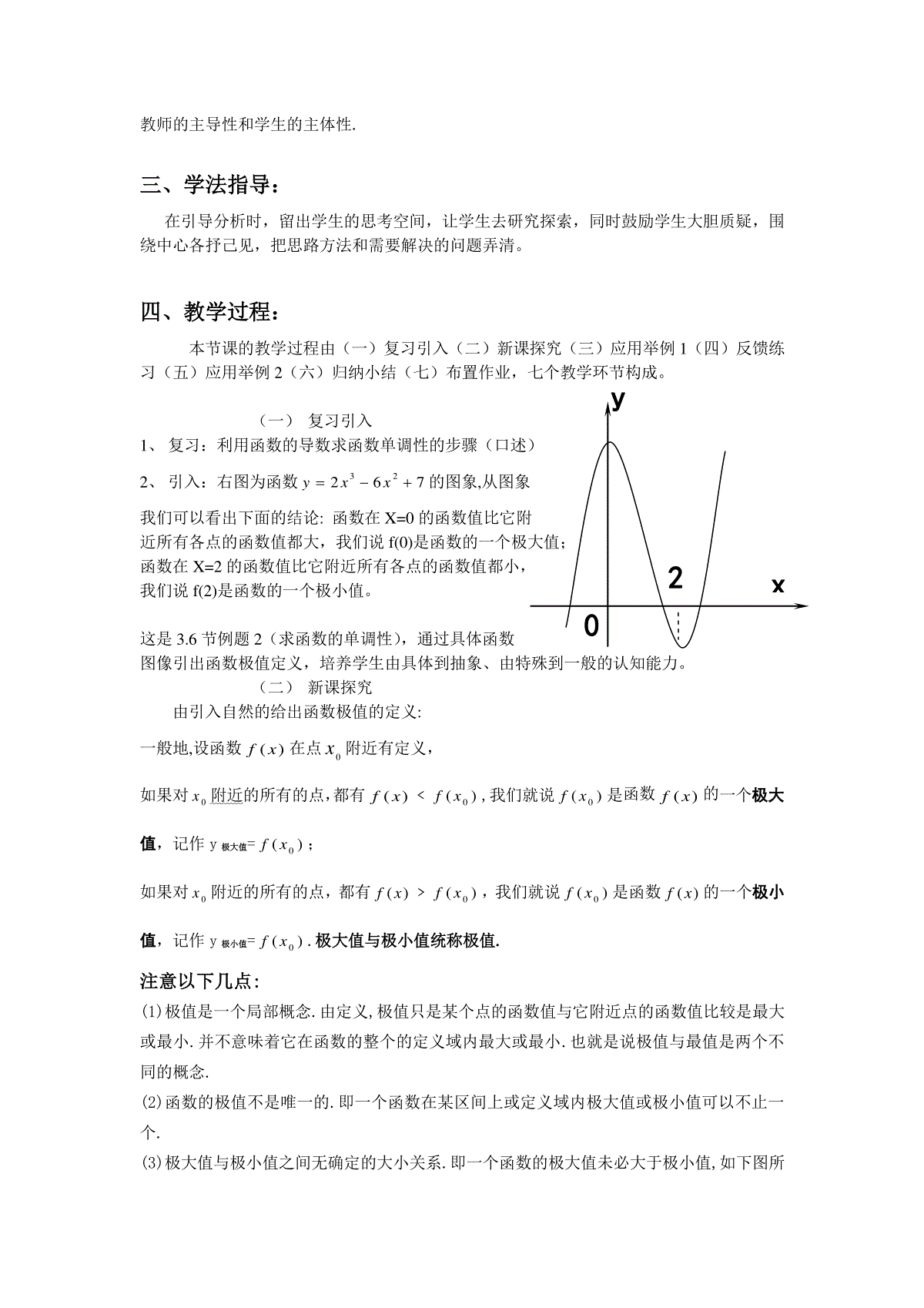
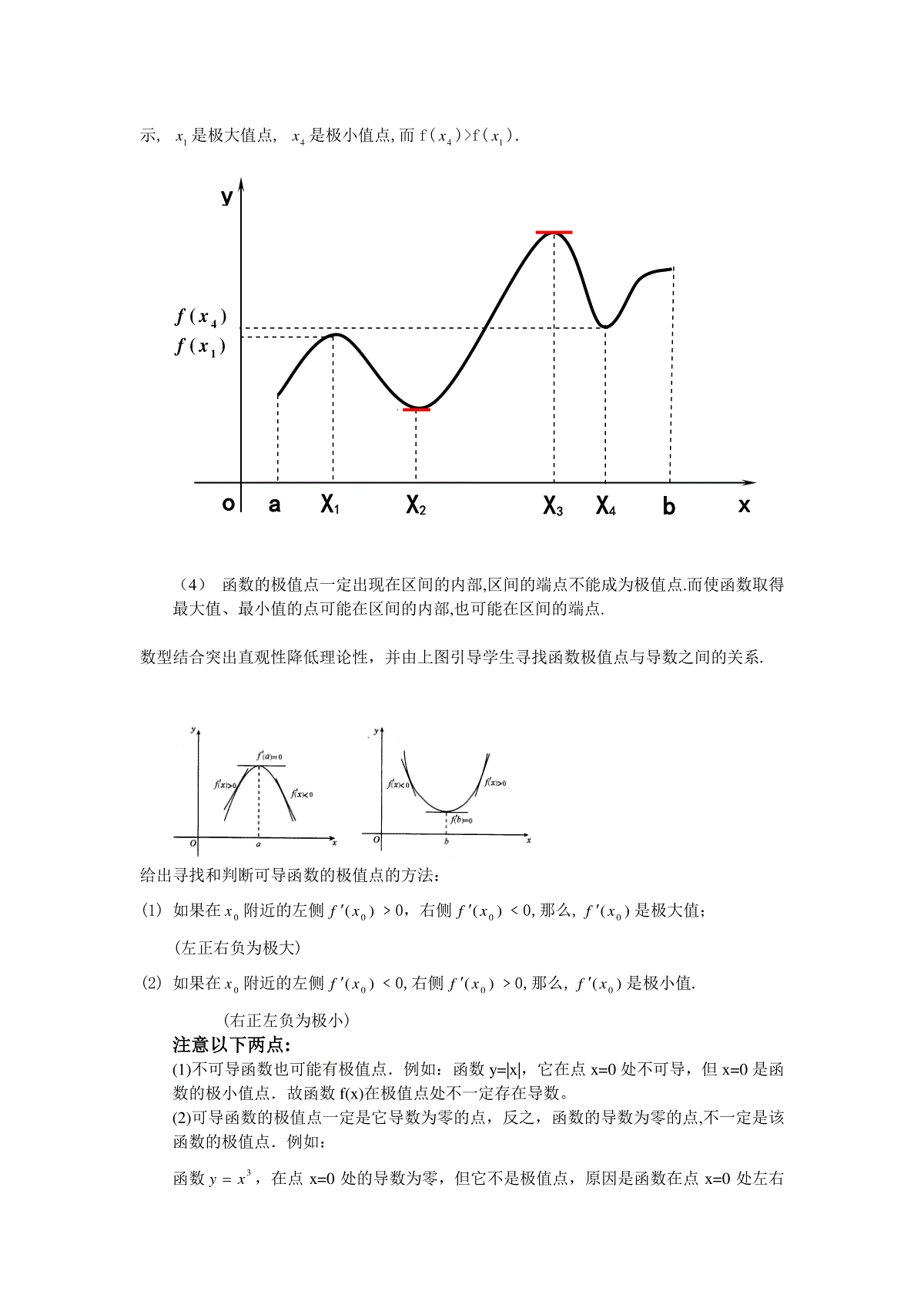
3．7函数的极值（说课稿）本节课讲述的是《人教版全日制普通高级中学教科书数学第三册（选修II）》§3.7函数的极值（第一课时）的内容。一、教材分析1、教材的地位和作用：本节课是导数应用中的第二节（第一节是利用导数知识判断函数的单调性），学生们已经了解了导数的一些用途，思想中已有了一点运用导数的基本思想去分析和解决实际问题的意识，本节课将继续加强这方面的意识和能力的培养——利用导数知识求可导函数的极值。其后还有利用导数求函数的最值问题、曲线的切线问题，利用导数研究不等式恒成立、方程根的讨论、函数图像交点等问题，因此本节课还要起到承上启下的作用。从高考角度分析，以中高档题为主，所以导数是非常重要的知识点。2、教学目标：（1）知识技能目标：掌握函数极值的定义，会从几何图形直观理解函数的极值与其导数的关系，增强学生的数形结合意识，提升思维水平；掌握利用导数求可导函数的极值的一般方法；了解可导函数极值点0x与)(0xf=0的逻辑关系；培养学生运用导数的基本思想去分析和解决实际问题的能力.（2）过程与方法目标：培养学生观察分析探究归纳得出数学概念和规律的学习能力。（3）情感与态度目标：培养学生层层深入、一丝不苟研究事物的科学精神；体会数学中的局部与整体的辨证关系.3、教学重点与难点：重点：掌握求可导函数的极值的一般方法.难点：0x为函数极值点与)(0xf=0的逻辑关系.二、学情教法分析：让学生掌握的重点内容：求可导函数的极值的方法和一般步骤，必须在课堂上就过手.由于学生对极限和导数的知识学习还谈不上深入细致，因此教学中更重视的是从感性认识到理性认识的探索过程，而略轻严格的理论证明.针对这一特点，本节课我采用师生互动探究式教学以及讲练结合的教学方法，通过问题激发学生求知欲，使学生主动参与，以独立思考和相互交流的形式，在教师的指导下发现、分析和解决问题。对于难点问题：0x为函数极值点与)(0xf=0的逻辑关系，可由教师层层递进性的主动提出，师生共同探究完成，体现教师的主导性和学生的主体性.三、学法指导：在引导分析时，留出学生的思考空间，让学生去研究探索，同时鼓励学生大胆质疑，围绕中心各抒己见，把思路方法和需要解决的问题弄清。四、教学过程：本节课的教学过程由（一）复习引入（二）新课探究（三）应用举例1（四）反馈练习（五）应用举例2（六）归纳小结（七）布置作业，七个教学环节构成。（一）复习引入1、复习：利用函数的导数求函数单调性的步骤（口述）2、引入：右图为函数32267yxx的图象,从图象我们可以看出下面的结论:函数在X=0的函数值比它附近所有各点的函数值都大，我们说f(0)是函数的一个极大值；函数在X=2的函数值比它附近所有各点的函数值都小，我们说f(2)是函数的一个极小值。这是3.6节例题2（求函数的单调性），通过具体函数图像引出函数极值定义，培养学生由具体到抽象、由特殊到一般的认知能力。（二）新课探究由引入自然的给出函数极值的定义:一般地,设函数)(xf在点0x附近有定义，如果对0x附近的所有的点，都有)(xf﹤)(0xf,我们就说)(0xf是函数)(xf的一个极大值，记作y极大值=)(0xf；如果对0x附近的所有的点，都有)(xf﹥)(0xf，我们就说)(0xf是函数)(xf的一个极小值，记作y极小值=)(0xf.极大值与极小值统称极值.注意以下几点:(1)极值是一个局部概念.由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小.并不意味着它在函数的整个的定义域内最大或最小.也就是说极值与最值是两个不同的概念.(2)函数的极值不是唯一的.即一个函数在某区间上或定义域内极大值或极小值可以不止一个.(3)极大值与极小值之间无确定的大小关系.即一个函数的极大值未必大于极小值,如下图所x0y2示,1x是极大值点,4x是极小值点,而f(4x)f(1x).（4）函数的极值点一定出现在区间的内部,区间的端点不能成为极值点.而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点.数型结合突出直观性降低理论性，并由上图引导学生寻找函数极值点与导数之间的关系.给出寻找和判断可导函数的极值点的方法：(1)如果在0x附近的左侧)(0xf﹥0，右侧)(0xf﹤0,那么,)(0xf是极大值；(左正右负为极大)(2)如果在0x附近的左侧)(0xf﹤0,右侧)(0xf﹥0,那么,)(0xf是极小值.(右正左负为极小)注意以下两点:(1)不可导函数也可能有极值点．例如：函数y=|x|，它在点x=0处不可导，但x=0是函数的极小值点．故函数f(x)在极值点处不一定存在导数。(2)可导函数的极值点一定是它导数为零的点，反之，函数的导数为零的点,不一定是该函数的极值点．例如：函数3yx，在点x=0处的导数为零，但它不是极值点，原因是函数在点x=0处左右oaX1X2X3X4baxy)(4xf)(1xf两侧的导数都大于零，因此导数为零的点仅是该点为极值点的必要条件，其充分条件是在这点两侧的导数异号。因此，利用求导的方法，求函数的极值时，在函数的定义域内寻求可能取到极值的“可疑点”，除了确定其导数为零的点外，还必须确定函数定义域内所有不可导的点，这两类点构成了函数定义域内所有的可能取到极值的“可疑点”。（三）应用举例1例１：求31443yxx的极值.教师讲解与板书解题过程,学生回答教师提出的相关问题。解:∵)(xf=x2-4,由)(xf=0解得x1=2,x2=-2.当x变化时,)(xf、)(xf的变化情如下表:x(-∞,-2）-2（-2,2）2(2,+∞）)(xf+00+)(xf极大值328极小值34当x=-2时,y极大值=328；当x=2时,y极小值=34.这是本节课的重点，利用导数知识求可导函数的极值.例题1的目的:得出求可导函数的极值的步骤：(1)求导数)(xf；(2)求方程)(xf=0的根；(3)检查)(xf在方程的根左右的值的符号.如果左正右负,那么)(xf在这个根处取极大值；如果左负右正,那么)(xf在这个根处取极小值.（四）反馈练习1、求出引例函数的极值，并给出答案2、P１４２练习（２）、（4）可仿例题1做并给出答案其中（2）为二次函数，也可由二次函数图像看出其极值3、（142页例题2）：求y=(x2-1)3+1的极值.（把例题2做课堂练习）仿例题1解答另提出思考问题：能否利用“数轴标根法”优化解题书写过程？)(xf=0的偶重根处是否是极值点？（画出几个图像：第一个数轴标根，第二个原函数图像，第三个导函数图像，利用导函数图像也可以得出是否取极值并可判断是极大还是极小值。）再次强调：要想知道0x是极大值点还是极小值点就必须判断)(0xf左右侧导数的符号。这是本节课的难点内容：利用函数极值点与)(0xf=0的逻辑关系解决多峰函数的极值问题.（五）应用举例2例题2：已知函数432()2fxxaxxb（xR），其中Rba,若函数()fx仅在0x处有极值，求a的取值范围；解：2()(434)fxxxax，显然0x不是方程24340xax的根．为使()fx仅在0x处有极值，必须24403xax成立，即有29640a．解些不等式，得3838a．这时，(0)fb是唯一极值．因此满足条件的a的取值范围是88[,]33．这是一道已知在某处取极值求参数的问题，目的是强调要想知道0x是否为极值点就必须判断)(0xf左右侧导数的符号（突出本节课的重点）（六）归纳小结可导函数的极值与导数的关系：1.函数的极值是就函数在某一点附近的小区间而言，在函数的整个定义区间内可能有多个极大值或极小值，且极大值不一定比极小值大；2.点是极值点的充分不必要条件是在这点两侧的导数异号；点是极值点的必要不充分条件是在这点的导数为0.（七）布置作业习题3.72选作1：已知)(xf=ax3+bx2+cx(a≠0)在x=1处取得极值,且)1(f=-1.(1)求a,b,c的值;(2)判断x=1时函数取极大值还是极小值,并说明理由.选作2：已知函数432()2fxxaxxb（xR），其中Rba,．（Ⅰ）当103a时，讨论函数()fx的单调性；（Ⅱ）若对于任意的[2,2]a，不等式1fx在[1,1]上恒成立，求b的取值范围．第二问是最值的应用，为下一节引出的课题.(局部与整体）适当分层让不同的人学习不同的数学.板书设计：3．7函数的极值1、函数的极值的定义2.判断可导函数极值的方法并给出简图4．求可导函数的极值的步骤:3．例题1求函数y=44313xx的极值（板书解题过程）5．例题2求y=（x2-1）3+1的极值。(学生口答,教师板书解题过程)并给出三个图像6．练习7．作业P143习题3.7,选作