向量法求夹角

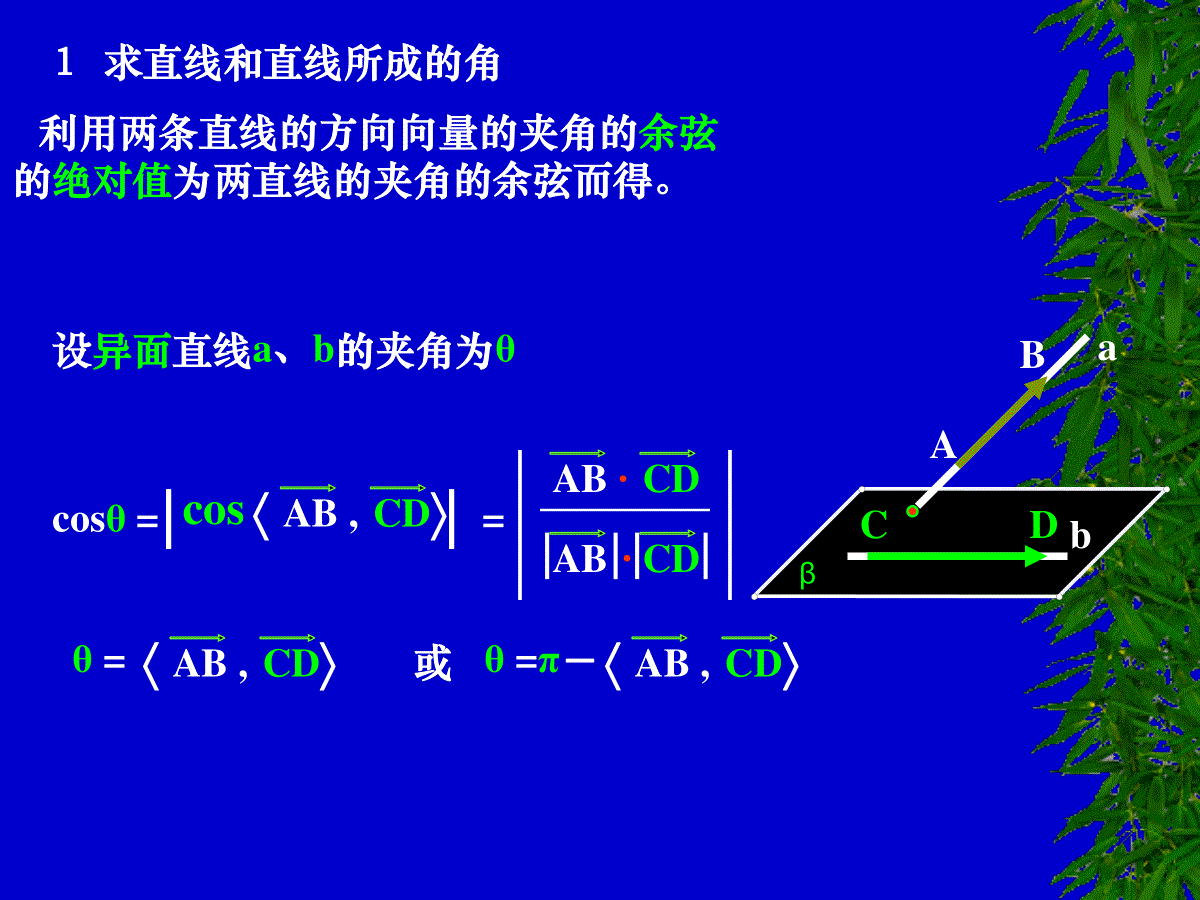
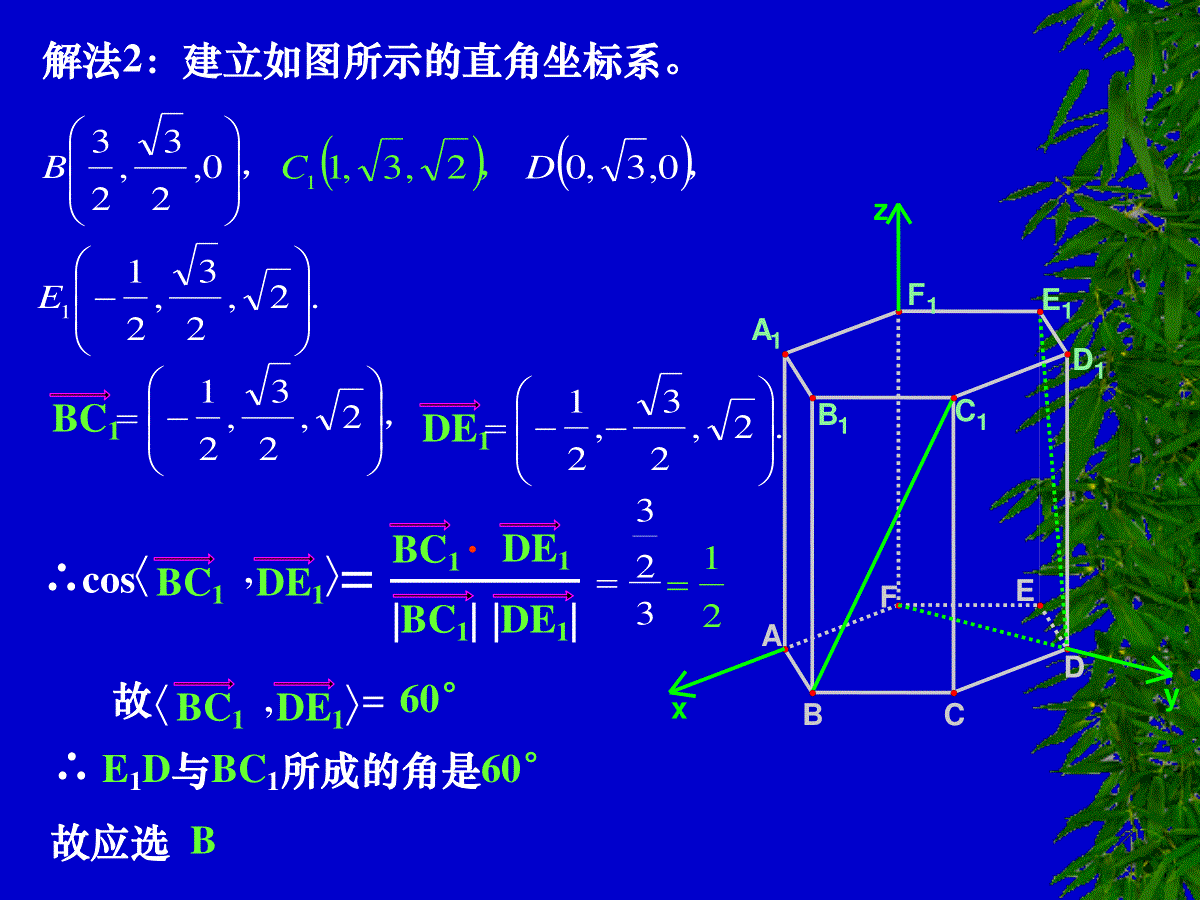
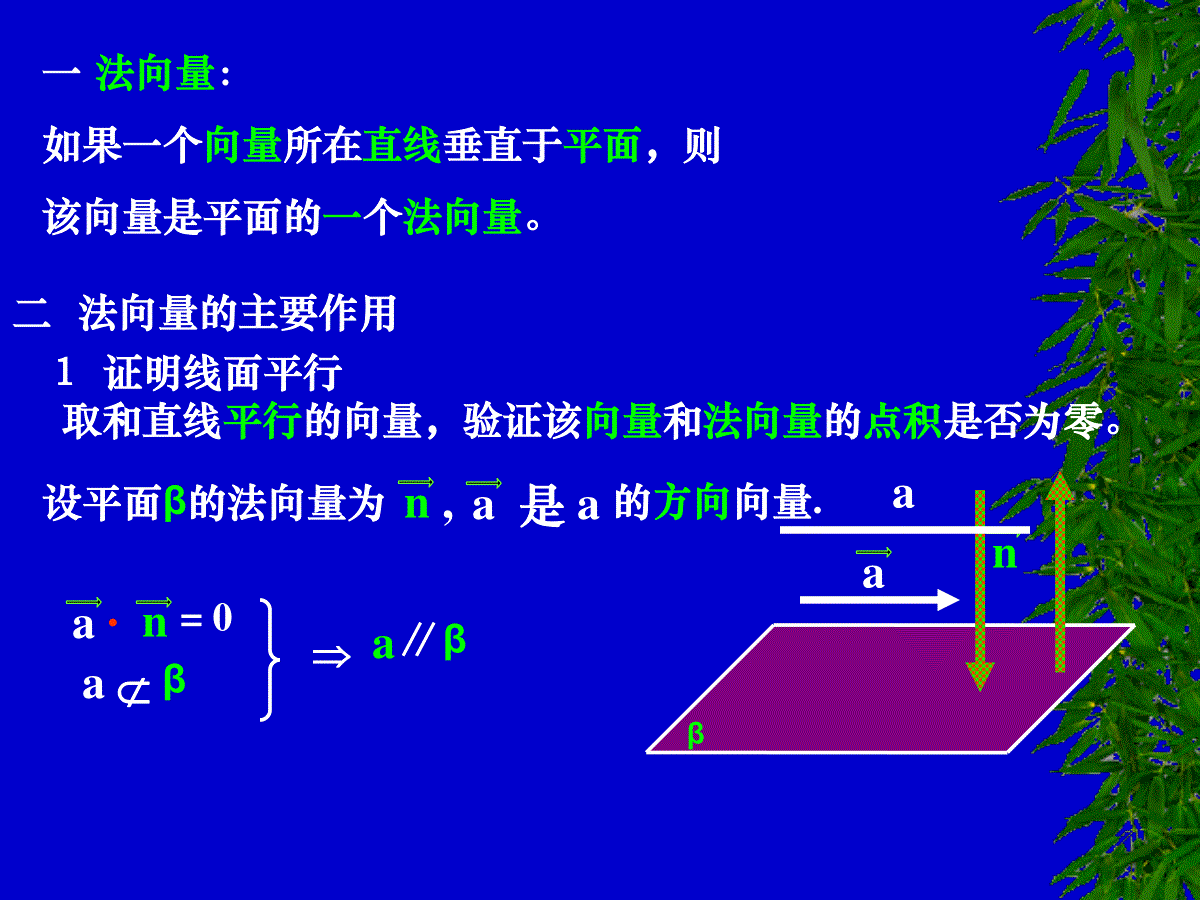
βabABCD设异面直线a、b的夹角为θcosθ=AB,CDcos||=AB·CD·AB||CD||θ=AB,CD或θ=π－AB,CD利用两条直线的方向向量的夹角的余弦的绝对值为两直线的夹角的余弦而得。1求直线和直线所成的角[例1]正六棱柱ABCDEF—A1B1C1D1E1F12的底面边长为1,侧棱长为,则这个棱柱的侧面对角线E1D与BC1所成的角是（）C1D1E1F1A1DBCFEAB1A.90°B.60°C.45°D.30°(2002年全国高考）解法一：连结FE1、FD、BC1∴四边形BFE1C1是平行四边形∴FE1∥BC1∴∠FE1D是异面直线E1D与BC1所成的角或补角∵底长为1，棱长为231DE=FE13DF又∴△FDE1为等边三角形∴∠FE1D=60°B解法2：建立如图所示的直角坐标系。C1D1E1F1A1DBCFEAB1zxy，0,23,23B，2,3,11C，0,3,0D.2,23,211EBC1，2,23,21DE1.2,23,21∴cos,=BC1DE1BC1·DE1|BC1||DE1|32321故,BC1DE1=60°∴E1D与BC1所成的角是60°故应选B一法向量：如果一个向量所在直线垂直于平面，则该向量是平面的一个法向量。1证明线面平行二法向量的主要作用取和直线平行的向量，验证该向量和法向量的点积是否为零。βa设平面β的法向量为n,na是a的方向向量.aa·n=0aβa∥β例1.如图,正方体ABCD——A1B1C1D1中,E是的BB1中点,求证:BD1∥平面A1C1ECDBAB1C1D1A1EO法一：证明：连B1D1交A1C1于O连OEOD1=OB1B1E=BEOE∥BD1BD1平面A1C1EOE平面A1C1EBD1∥平面A1C1EECDC1D1BAA1B1zxy证法二：如图所示建立直角坐标系,且设正方体的棱长为2,D1(0,0,0),B(2,2,2),A1(2,0,0),C1(0,2,0),E(2,2,1)D1B∴=(2,2,2)A1E=(0,2,1)C1E=(2,0,1)设平面A1EC1的法向量为n=(x,y,z)∴nA1E·=2y+z=0nC1E·=2x+z=0令x=1时，z=－2，y=1n=(1,1,－2)∴D1B·∴n=0D1B⊥nD1B平面A1EC1D1B∥平面A1EC1β2证明面面垂直如图设n1,n2分别是平面、β的法向量n1n2n1·n2=0当时a⊥β验证两个平面的法向量的点积是否为零。3、求直线和平面所成的角βCBθn设直线BA与平面β的夹角为θ，n为平面β的法向量,Ag1n与向量BA的夹角为锐角g1当12gθ=βCBAθng2n与向量BA的夹角为钝角g2当22gθ=BACOEF例1如图所示,已知正四面体O—ABC，E、F分别是AB、OC的中点。(1)求OE与BF所成的角；（2）求BF与平面ABC所成的角。分析:(1)设OA=caOB=bOC=abc求出OE,BF,然后可求cosOE,BFBFOE·||OE||BF=(2)可过点O作OO’⊥平面ABC于点O’，O'若OO’与BF所成的角为θ20，则BF与平面ABC所成的角为2BACOEFabc解:(1)设正四面体O—ABC的棱长为1,OA=caOB=bOC=则a·b=c·b=a·c21||=1a||=||=bcOE21(+)abBF21c－bOE·BF=21(+)·ab()21c－b21(21a·c+21cb·a·b－||2b－)12141412121cosOE,BFBFOE·||OE||BF=23232132∴OE与BF所成的角为32arccos2BACOEFabc（2）求BF与平面ABC所成的角。BACOEFabc(2)作OO’⊥平面ABC于点O’，设OO’与BF所成的角为θ20,则BF与平面ABC所成的角为2O'OO’=OC+CO’c=32CEc=32()OE－OCc=[]21(+)－ab32c31(+)abc+BACOEFabcO'||2OO’91(+)2abc+(+)91|a|2|b|2+|c|2+2a·bc·b+2+2a·c339132∴||OO’36cos=OO’,BFBFOO’·||OO’||BF=()21c－b31(+)·abc+2336cbbbaccbca2221212132BACOEFabcO'cbbbaccbca2221212132cosOO’,BF21121214141323232arccos∴求BF与平面ABC所成的角32arccos232arcsin评析:利用向量讨论线面关系不需作辅助线，但需要正确设出空间向量的基底，再利用多面体的性质算出或找出其它的向量。baln1n2g4.法向量的夹角与二面角的平面角的关系设,=gn1n2设a—l—b的平面角为－gbaln1n2gg两个平面的法向量同时指向或背离。baln1n2gbaln1n2g设,=gn1n2设a—l—b的平面角为g两个平面的法向量一个指向另一个背离。例1如图,在棱长为1的正方体ABCD—A1B1C1D1中,AC与BD交于点E,C1B与CB1交于点F.(1)求证：A1C⊥平面BDC1(2)求二面角B—EF—C的大小(结果用反三角函数表示)证明:(1)以点D为坐标原点建立如图所示的空间直角坐标系,则FEC1D1CDB1A1BAzxyC(0,1,0),A1(1,0,1),B(1,1,0),D(0,0,0),C1(0,1,1),A1C=(－1,1,－1),C1D=(0,－1,－1),BD=(－1,－1,0)A1C·C1D=0－1+1=0A1C⊥C1DA1C·BD=1－1+0=0A1C⊥BDC1D∩BD=DA1C⊥平面BDC1解:(2)同（1）可知,D1B⊥平面AB1CzxyEFC1D1CDB1A1AB由(1)A1C⊥平面BDC1即向量D1B是平面AB1C的一个法向量。,A1C是平面BDC1的一个法向量。A1C=(－1,1,－1),∵D1B=(1,1,－1),cos,A1CD1BA1C·D1B=||A1C·D1B||31故二面角B—EF—C的为31arccos例2.(2001年全国）如图,在底面是直角梯形的四棱锥S—ABCD中,.21AD与面SBA所成的二面角的正切值。DBCAs解法1：延长BA、CD相交于E,E连接SE,则SE是所求二面角的棱AD∥BCBC=2ADEA=AB=SASE⊥SBSA⊥面ABCDSA⊥BCBC⊥ABBC⊥面SEB∴SB是SC在面SEB上的射影。∠ABC=90°,SA⊥面ABCD,求面SCDSA=BC=AB=1,EDBCAs∴SC⊥SE∴∠CSB是所求二面角的平面角.22ABSASB2BC=1∠SBC=90°tan∠BSCSBBC22即所求二面角的正切值为22DBCAszxy解法2：建立如图所示的直角坐标系0,0,21D则,C(1,1,0),S(0,0,1)AD0,0,21且AD是面SBA的法向量设平面SCD的法向量n=(x,y,z)DC0,1,21SD1,0,21n·DC=0n·SD=0即021yx021zxDBCAszxy即021yx021zx令x=1,则，21y21zn∴21,21,1∴cosa=n·AD|n|·|AD|36从而tana22反思研究：求二面角大小可转化为求两个平面的法向量的夹角大小，两平面法向量的夹角与二面角的大小相等或互补，解题时要注意结合题目条件进一步确定二面角的大小。例3(2001年天津）如图,以正四棱锥V—ABCD底面中心O为坐标原点建立空间直角坐标系O—xyz,其中ox∥BC,oy∥AB,E为VC的中点,正四棱锥底面边长为2a,高为h.(1)求cosBE,DE（2）记面BCV为a,面DCV为b,∠BED是二面角a—VC—b的平面角,求∠BED。zyxOCDAVEB解:(1)依题意:B(a,a,0),C(－a,a,0),D(－a,－a,0)2,2,2haaEBE∴2,2,23haaDE2,23,2haazyxOCDAVEBBE∴2,2,23haaDE2,23,2haa∴BE·DE42322ha||BE又2222223haa221021ha||DE2222223haa221021hacos=BE,DE∴DEBE·||BE||DE2222106hahazyxEOCDBAV(2)∵∠BED是二面角a—VC—b的平面角BE⊥∴CVBE·CV=0又由C(－a,a,0),V(0,0,h)CV=(a,－a,h),∴BE又2,2,23haaBE·CV∴2223222haa=0ah2cosBE,DE∵2222106hahacosBE,DE∴222221026aaaa31∴∠BED=BE,DE31arccos31arccos[巩固练习]例1(2002年新教材高考题)如图所示,正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为a2(1)建立适当的坐标系,并写出点A、B、A1、C1的坐标；(2)求AC1与侧面ABB1A1所成的角。11ACBBCA1解:(1)如图以点A为坐标原点O,以AB所在的直线为oy轴,y以AA1所在直线为oz轴,z以经过原点且与平面ABB1A1垂直的直线为ox轴,建立空间直角坐标系,由已知得xA(0,0,0),B(0,a,0)A1(0,0,)a2aaaC2,2,231zxyACBB1C1A1(2)取A1B1的中点M,于是有MaaM2,2,0连MC1、AM,有MC10,0,23aAB=(0,a,0),AA1a2,0,0由于MC1·AB=0MC1·AA1=0∴MC1⊥平面ABB1A1∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角。AC1∵aaa2,2,23aaa2,2,23AMaa2,2,0AC1·∴AM22240aa249azxyACBB1C1A1MAC1∵AMaa2,2,0AC1·∴AM22240aa249aaaa2,2,23|AC1|又2222443aaaa3|AM|2224aaa23cos,=AC1AM249aa3a2323∴AC1与侧面ABB1A1所成的角为30°评析:本题主要考查空间直角坐标系的概念，空间点和向量的坐标表示以及向量夹角的计算方法，考查运用向量研究空间图形的数学思想方法。B1C1BA1C例2(2003年全国)如图直三棱柱ABC—A1B1C1底面是等腰直角三角形,ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.求A1B与平面ABD所成的角的大小(结果用反三角函数值表示)AEDG解:连结BG,则BG是BE在面ABD上的射影即A1BG是A1B与ABD所成的角。如图所示建立直角坐标系,坐标原点为C设CA=2a,则A(2a,0,0),B(0,2a,0),D(0,0,1),E(a,a,1),31,32,32aaG32,3,3