11.2探索三角形全等的条件SAS

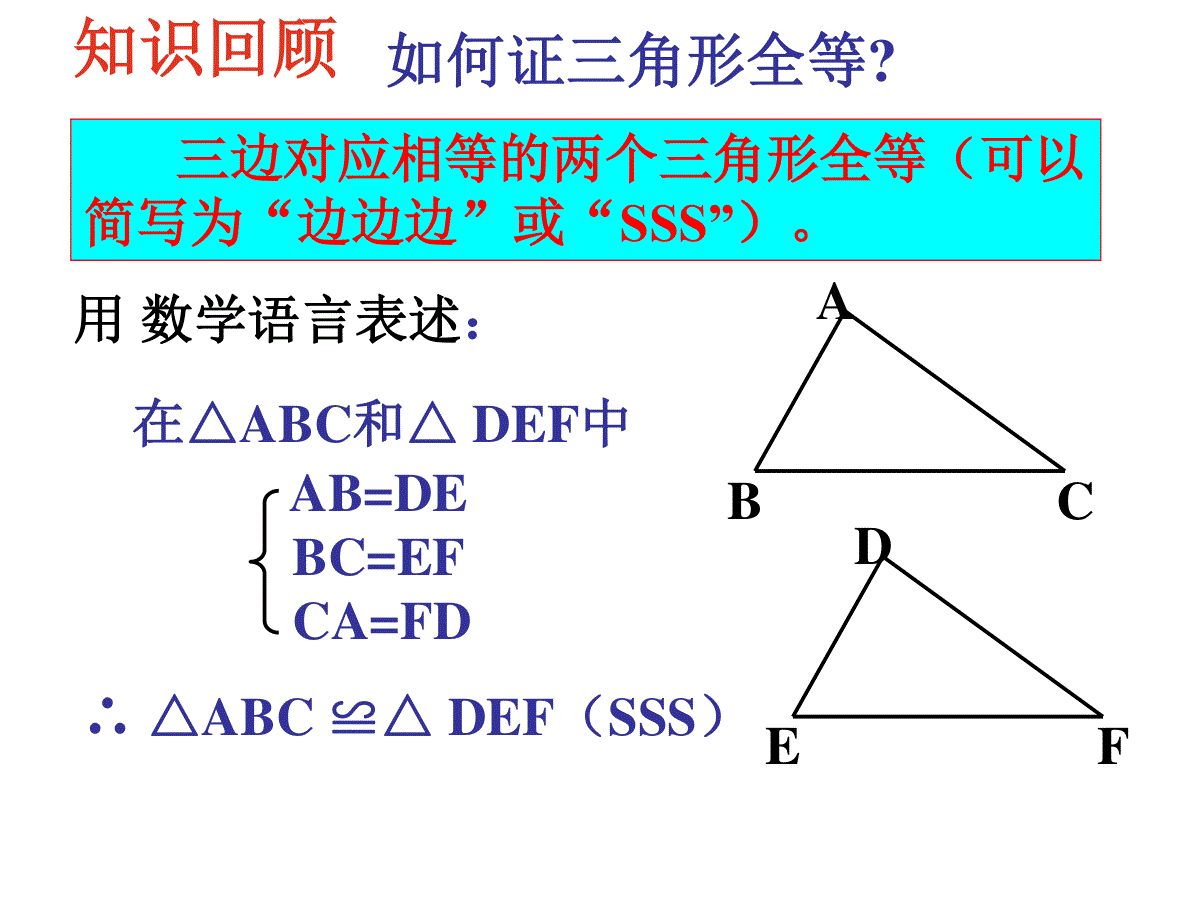
创设情景因铺设电线的需要，要在池塘两侧A、B处各埋设一根电线杆（如图），因无法直接量出A、B两点的距离，现有一足够的米尺。怎样测出A、B两杆之间的距离呢？。AB知识回顾三边对应相等的两个三角形全等（可以简写为“边边边”或“SSS”）。ABCDEF用数学语言表述：在△ABC和△DEF中∴△ABC≌△DEF（SSS）AB=DEBC=EFCA=FD如何证三角形全等?作一个角等于已知角已知:∠AOB，求作:∠A′O′B′,使∠A′O′B′=∠AOBBAO作法:1.以点O为圆心,任意长为半径画弧,分别交OA，OB于点C，D；2.画一条射线O′A′，以点O′为圆心，OC长为半径画弧，交O′A′于点C′3.以点C′为圆心，CD长为半径画弧，与前弧交于点D′4.过点D′画射线O′B′。∴∠A′O′B′就是所求的角。先任意画出一个△ABC，再画出一个△A′B′C′使A′B′=AB，A′C′=AC，∠A=∠A′。画法：2.在射线A′D上截取A′B′=AB3.在射线A′E上截取A′C′=AC1.画∠DA′E=∠A4.连接B′C′∴△A′B′C′就是所求的三角形把你们所画的三角形剪下来与原来的三角形进行比较，它们能互相重合吗？探究1三角形全等判定方法2用符号语言表达为：在△ABC与△DEF中AB=DE∠B=∠EBC=EF∴△ABC≌△DEF（SAS）ABCDEF两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”例1.(1)如图，AC=BD，∠CAB=∠DBA，你能判断BC=AD吗？说明理由。ABCD证明:在△ABC与△BAD中AC=BD∠CAB=∠DBAAB=BA∴△ABC≌△BAD（SAS）(已知)(已知)(公共边)例题欣赏∴BC=AD（全等三角形的对应边相等）(2).如图，在△AEC和△ADB中，已知AE=AD，AC=AB请说明△AEC≌△ADB的理由。AE=AD(已知)=()AC=AB(已知)AEBDCSAS解：在△AEC和△ADB中例题欣赏∴△AEC≌△ADB（）∠A∠A公共角因铺设电线的需要，要在池塘两侧A、B处各埋设一根电线杆（如图），因无法直接量出A、B两点的距离，现有一足够的米尺。请你设计一种方案，粗略测出A、B两杆之间的距离。。AB小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结DE，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。AC=DC∠ACB=∠DCEBC=EC∴△ACB≌△DCE∴AB=DE在△ACB和△DCE中结论：两边及其中一边的对角对应相等的两个三角形不一定全等探究2如图△ABC与△ABD中，AB=AB，AC=AD，∠B=∠B△ABC与△ABD全等吗？BACD我们知道，两边和它们的夹角对应相等的两个三角形全等，由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗？为什么？1.如图，AE=AF,∠AEF=∠AFE,BE=CF,求证：AB=ACABCEF练习：1.如图，两车从南北方向的路段AB的一端A出发，分别向东、向西行进相同的距离，到达C、D两地，此时C、D到B的距离相等吗？为什么？ACDB1、已知：如图AB=AC,AD=AE,∠BAC=∠DAE求证：∠B=∠CABDCE2.如图，点E、F在BC上，BE=CF，AB=CD，∠B=∠C，求证：∠A=∠DEABFCD(1)已知：如图，AB=CB，∠ABD=∠CBD。问AD=CD，BD平分∠ADC吗？ABCD(2)已知:AD=CD，BD平分∠ADC。问∠A=∠C吗？木棒刻度尺提供工具:两条等长木棒(足够长),刻度尺ABDCO如何来测量工件内槽的宽度呢?ABODC两边及一角对应相等的两个三角形全等吗？①两边及夹角对应相等的两个三角形全等（SAS)；②两边及其中一边的的对角对应相等的两个三角形不一定全等．③现在你知道哪些三角形全等的判定方法？SSS,SAS我思我能行1、今天我们学习哪种方法判定两三角形全等？边角边（SAS）2、通过这节课，判定三角形全等的条件有哪些？SSS、SAS、注意哦！“边边角”不能判定两个三角形全等驶向胜利的彼岸反思小结