平行线的判定与性质复习ppt课件

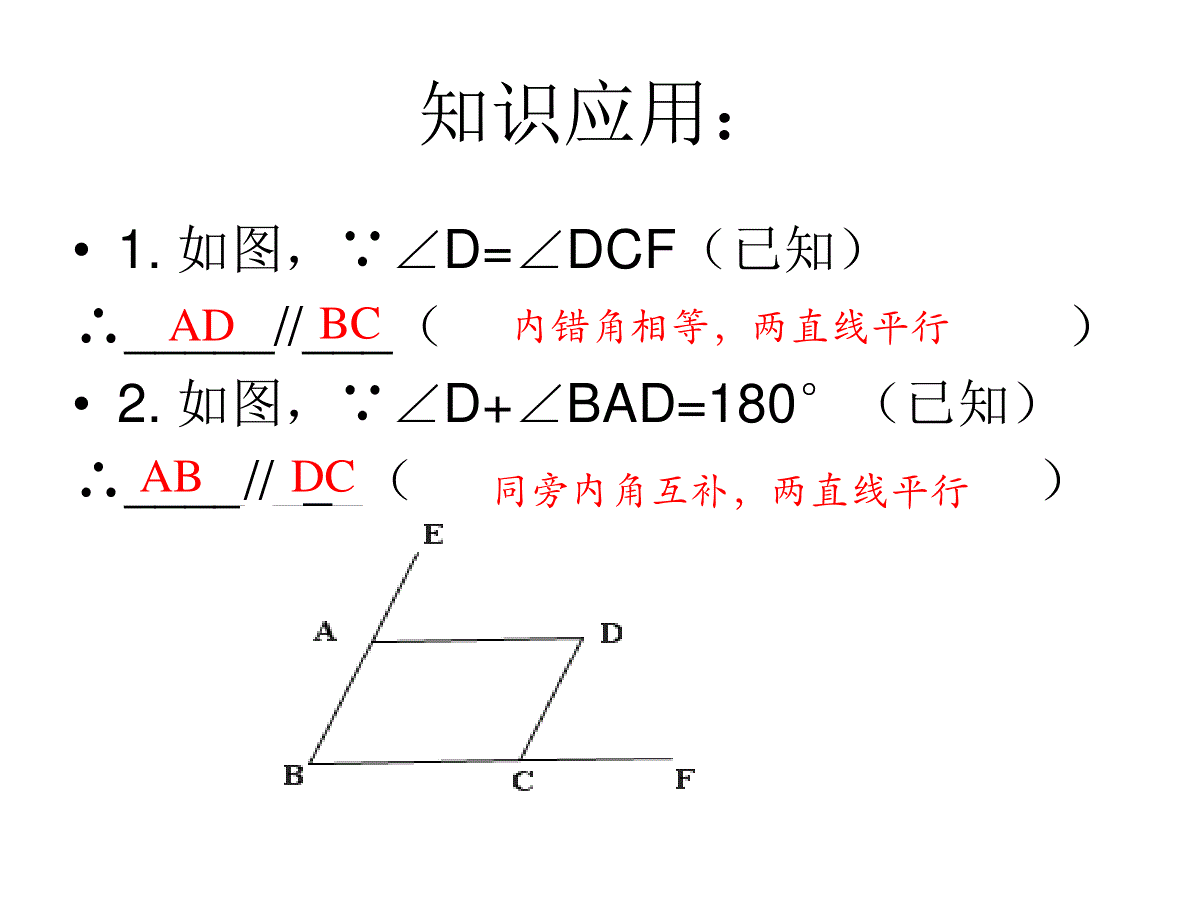
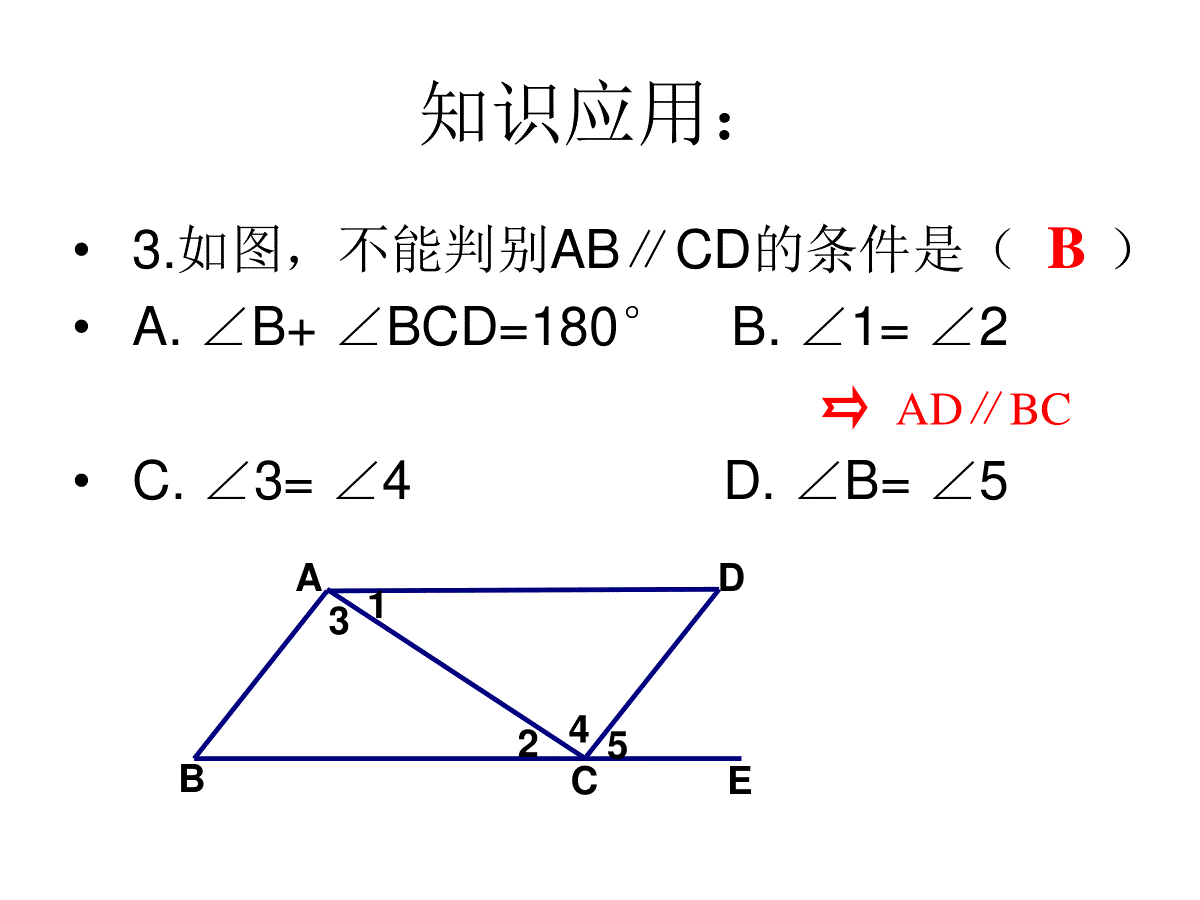
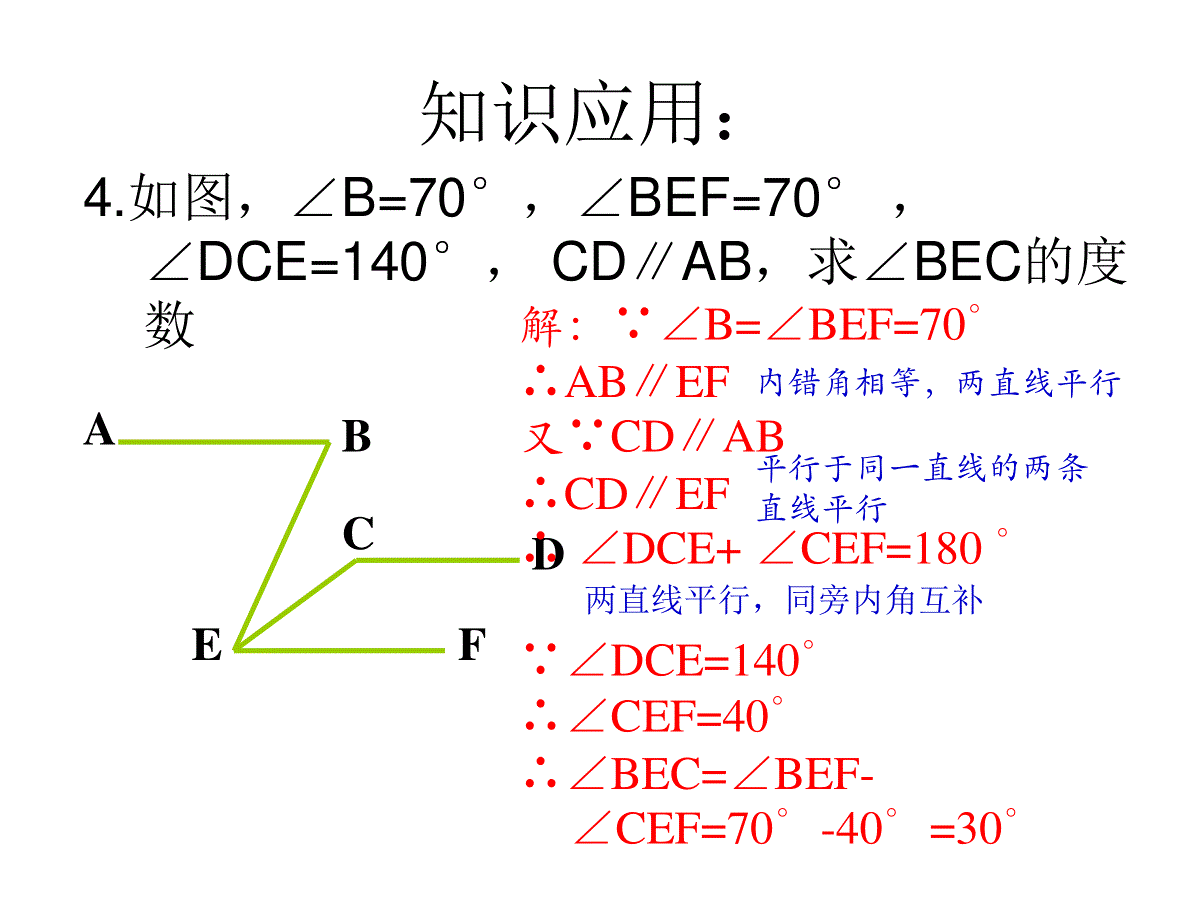
平行线的判定与性质复习课平行线的判定与性质平行线的判定平行线的性质1、平行线的定义：在同一平面内，不相交的两条直线互相平行。2、平行线的传递性：平行于同一条直线的两条直线平行3、平行线的判定公理：同位角相等，两直线平行4、平行线的判定定理1：内错角相等，两直线平行5、平行线的判定定理2：同旁内角互补，两直线平行5.平行线的判定推论：垂直于同一条直线的两条直线互相平行1、根据平行线的定义：在同一平面内，互相平行的两条直线没有交点2、平行线的性质公理：两直线行，同位角相等3、平行线的性质定理1：两直线平行，内错角相等4、平行线的性质定理2：两直线平行，同旁内角互补5、平行线间的距离：从一条直线上一点到另一条直线的垂线段的长度知识应用：•1.如图，∵∠D=∠DCF（已知）∴_____//___（）•2.如图，∵∠D+∠BAD=180°（已知）∴____//__（）ADBCABDC内错角相等，两直线平行同旁内角互补，两直线平行知识应用：•3.如图，不能判别AB∥CD的条件是（）•A.∠B+∠BCD=180°B.∠1=∠2•C.∠3=∠4D.∠B=∠554321EDCBABAD∥BC知识应用：4.如图，∠B=70°，∠BEF=70°，∠DCE=140°，CD∥AB，求∠BEC的度数EACFBD解：∵∠B=∠BEF=70°∴AB∥EF又∵CD∥AB∴CD∥EF∴∠DCE+∠CEF=180°∵∠DCE=140°∴∠CEF=40°∴∠BEC=∠BEF-∠CEF=70°-40°=30°内错角相等，两直线平行平行于同一直线的两条直线平行两直线平行，同旁内角互补知识应用：•5.如图，AB∥CD，EF分别交AB、CD于M、N，∠EMB=50°，MG平分∠BMF，MG交CD于G，求∠1的度数.ABCDEMNFG1解：∵∠EMB=50°∴∠BMF=180°-∠EMB=130°∵MG平分∠BMF∴∠BMG=1/2∠BMF=65°∵AB∥CD∴∠1=∠BMG=65°邻补角定义已知角平分线定义已知两直线平行，内错角相等知识应用：6.如图，已知DE、BF分别平分∠ADC和∠ABC，∠1=∠2，∠ADC=∠ABC.•试说明AB∥CD.ADBCFE123解：∵DE、BF分别平分∠ADC和∠ABC∴∠3=1/2∠ADC，∠2=1/2∠ABC又∵∠ADC=∠ABC∴∠3=∠2∵∠1=∠2∴∠1=∠3∴AB∥CD已知角平分线定义已知等量代换内错角相等，两直线平行C=DA=FDFACD=41=31=22=3DBEC4=CC=D解：∥∥已知理由是内错角相等，两直线平行两直线平行，内错角相等对顶角相等已知等量代换同位角相等，两直线平行两直线平行，同位角相等等量代换0CDABEFABCDB=EFB=90CDEF3=21=21=3DGBCAGD=ACB解：，∥∥同位角相等，两直线平行两直线平行，同位角相等已知等量代换内错角相等，两直线平行两直线平行，同位角相等垂直定义000ABCDBMN+MND=180MGNGBMNMND11NMG=BMNMNG=MND22NMG+MNG=90MGN=90MGNG证明：∥、分别平分和，