【全优课堂】2014年秋高中数学-2.1.3-4平面与平面之间的位置关系课件-新人教A版必修2

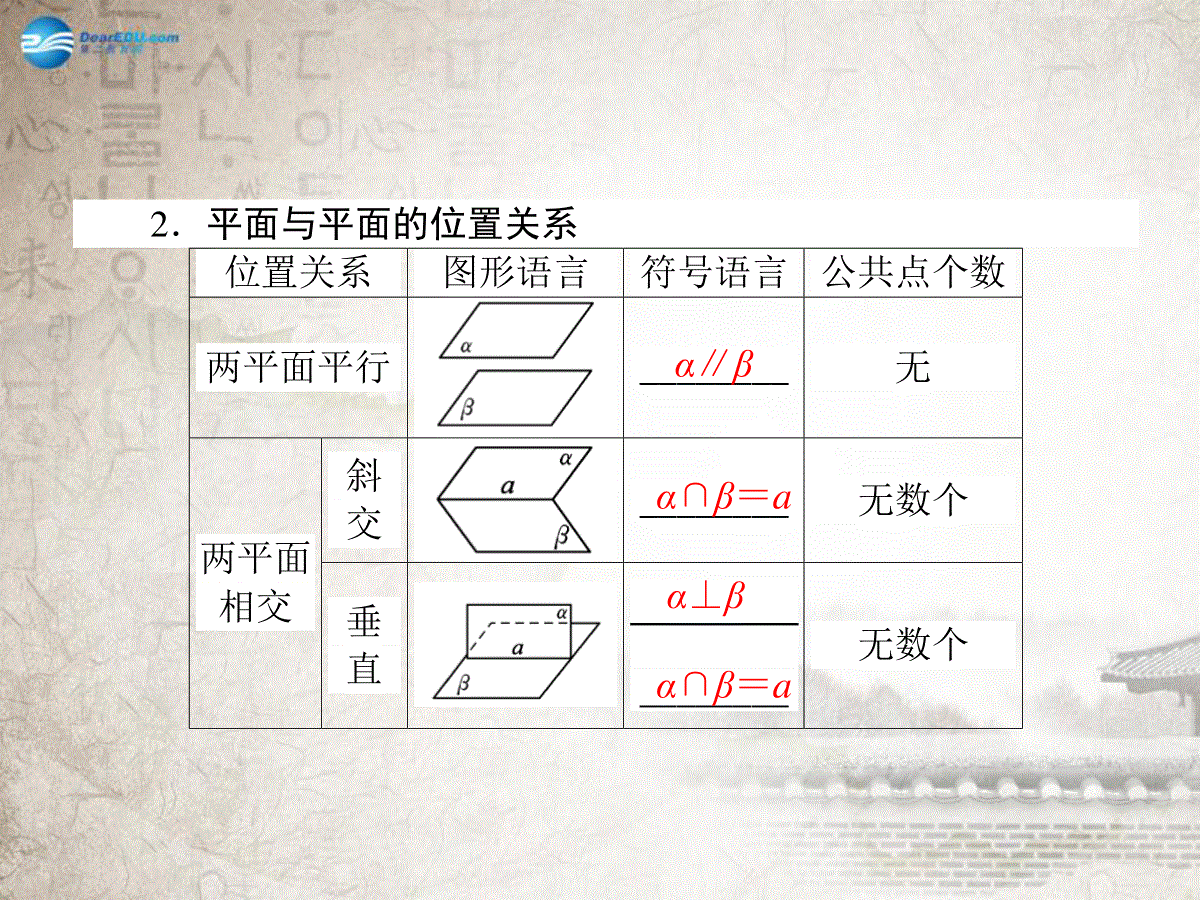
自学导引1．直线与平面的位置关系直线与平面的位置关系定义图形语言符号语言直线在平面内____________________直线与平面相交____________________直线与平面平行____________________有无数个公共点a⊂α有且只有一个公共点a∩α＝A没有公共点a∥α2．平面与平面的位置关系位置关系图形语言符号语言公共点个数两平面平行________无斜交________无数个两平面相交垂直________无数个α∥βα∩β＝aα⊥βα∩β＝a自主探究探究1：若直线a与平面α平行，是不是平面α内的所有直线都与a平行？探究2：“a⊄α”的含义是什么？【答案】不是，若a∥α，在平面α内的直线可能与a平行，也可能与a异面．【答案】a⊄α包含两种情况，一种是a∥α，另一种是a与α相交．预习测评1．过平面外一点，可作这个平面的平行线条数为()A．1条B．2条C．无数条D．不确定【答案】C2．如果在两个平面内分别有一条直线，这两条直线互相平行，那么这两个平面的位置关系一定是()A．平行B．相交C．平行或相交D．垂直相交【答案】C3．空间三个平面如果每两个都相交，那么它们的交线有________条．4．经过平面外两点可作这个平面的平行平面的个数是________．【答案】1或3【答案】至多可以作一个要点阐释1．直线和平面的位置关系(1)按公共点个数分类直线和平面平行直线和平面不平行直线和平面相交直线在平面内(2)按是否在平面内分类直线在平面内直线不在平面内直线和平面相交直线和平面平行2．两个平面的位置关系(1)两个平面的位置关系：两个平面的位置关系同平面内两条直线的位置关系相类似，可以从有无公共点来区分．如果两个平面有一个公共点，那么由公理3可知：这两个平面相交于过这个点的一条直线；如果两个平面没有公共点，那么就说这两个平面互相平行．(2)两个平面位置关系的画法：两个平行平面的画法：画两个平行平面时，要注意把表示平面的平行四边形画成对应边平行，如图(1)，而图(2)的画法是不恰当的．两个相交平面的画法：①先画表示两个平面的平行四边形的相交两边，如图(a)．②再画出表示两个平面交线的线段，如图(b)．③过图(b)中线段的端点分别引线段，使它们平行于图(b)中表示交线的线段，如图(c)．④画出图(c)中表示两个平面的平行四边形的第四边(被遮住的线，可以画成虚线，也可以不画)，如图(d)．图(a)图(b)图(c)图(d)典例剖析题型一直线与平面、平面与平面位置关系的画法【例1】指出图中的图形画法是否正确，若不正确，请你画出正确图形．思路点拨：注意虚实线的区分．【解析】(1)(2)(3)(4)的图形画法都不正确，正确画法如图所示．1．作出下列各小题的图形．(1)画直线a，b，使a∩α＝A，b∥α；(2)画平面α，β，γ，使α∥β，γ∩α＝m，γ∩β＝n；(3)画平面α，β，直线a，b，使α∩β＝l，a⊂α，b⊂β，且a∥β，b∩α＝B.【解析】题型二直线与平面的位置关系【例2】以下命题(其中a，b表示直线，α表示平面)，①若a∥b，b⊂α，则a∥α；②若a∥α，b∥α，则a∥b；③若a∥b，b∥α，则a∥α；④若a∥α，b⊂α，则a∥b.其中正确命题的个数是()A．0个B．1个C．2个D．3个思路点拨：本题解题的关键是判断直线与平面的公共点的个数．【解析】如图，在长方体ABCD－A′B′C′D′中，AB∥CD，AB⊂平面ABCD，但CD⊂平面ABCD，故①错误；A′B′∥平面ABCD，B′C′∥平面ABCD，但A′B′与B′C′相交，故②错误；AB∥A′B′，A′B′∥平面ABCD，但AB⊂平面ABCD，故③错误；A′B′∥平面ABCD，BC⊂平面ABCD，但A′B′与BC异面，故④错误．【答案】A2．对于任意的直线l和平面α，在平面α内必有直线m，使m和l()A．平行B．相交C．垂直D．异面【答案】C题型三平面与平面之间的位置关系【例3】在以下四个命题中，正确的命题是()①平面α内有两条直线和平面β平行，那么这两个平面平行；②平面α内有无数条直线和平面β平行，则α与β平行；③平面α内△ABC的三个顶点到平面β的距离相等，则α与β平行；④平面α内的两条相交直线和平面β内的两条相交直线分别平行，则α与β平行．A．③④B．②④C．②③④D．④思路点拨：两平面平行，一个平面的任意一条直线都与另一个平面平行．【解析】如图，正方体ABCD－A1B1C1D1中，对于①，平面A1D1DA中，AD∥平面A1B1C1D1，分别取AA1，DD1的中点E，F，连接EF，则知EF∥平面A1B1C1D1.但平面AA1D1D与平面A1B1C1D1是相交的，交线为A1D1，故命题①错．对于②，在正方体ABCD－A1B1C1D1的面AA1D1D中，与AD平行的直线有无数条，但平面AA1D1D与平面A1B1C1D1不平行，而是相交于直线A1D1，故②是错误的．对于③，在正方体ABCD－A1B1C1D1中，分别取AA1，DD1，BB1，CC1的中点E，F，G，H，A1，B，C到平面EFHG的距离相等，而△A1BC与平面EFHG相交，故③是错误的．命题④是正确的，故选D.【答案】D方法点评：构造相关图形，利用空间图形的形象、直观来说明两个平面的位置关系，说服力强，令人信服，需要注意的是在作图时必须把问题涉及的各种情况都考虑清楚，而无遗漏．利用正方体(或长方体)这个“百宝箱”能有效地判定与两个平面的位置关系有关命题的真假，因此我们要灵活地运用这个“百宝箱”来判定两个平面的位置关系．另外，像判定直线与直线、直线与平面的位置关系一样，反证法也是判定两个平面位置关系的有效方法，特别是在刚刚接触它之时.3．若直线a⊂平面α，直线b⊂平面β，a，b是异面直线，则α，β的位置关系是________．【答案】平行或相交误区解密判断直线与平面位置关系时因漏掉直线在平面内而出错【例4】下列命题：①若直线l与平面α内的无数条直线平行，则l∥α；②若直线a在平面α外，则a∥α；③若直线a∥b，直线b⊂α，则a∥α；④若直线a∥b，b⊂α，那么直线a就平行于平面α内的无数条直线．其中真命题的个数为()A．1个B．2个C．3个D．4个错解：C错因分析：对于①，直线l虽与平面α内的无数条直线平行，但l有可能在平面α内，∴l不一定平行于α，∴①是假命题．对于②，∵直线a在平面α外，包括两种情况：a∥α和a与α相交，∴a和α不一定平行，∴②是假命题．对于③，∵直线a∥b，b⊂α，则只能说明a和b无公共点，但a可能在平面α内，∴a不一定平行于α，∴③是假命题．对于④，∵a∥b，b⊂α，那么a⊂α或a∥α，∴a与平面α内的无数条直线平行，∴④是真命题．综上，真命题的个数为1个．正解：A纠错心得：在研究直线与平面的位置关系时，一定要真正理解相关概念．实际上，直线与平面相交，要求直线与平面有且只有一个公共点，即直线与平面有一个公共点且直线不在平面内，也即直线既不与平面平行，又不在平面内．直线与平面不相交，即直线与平面平行，或者直线在平面内．课堂总结1．直线与平面的位置关系有且只有三种：直线在平面内、直线与平面相交、直线与平面平行．后面两种关系又统称为直线在平面外．2．两个平面的位置关系有两种：两个平面平行，两平面相交．3．在判断直线与平面的位置关系中：判断直线在平面内时，常用公理1和反证法．判断直线和平面相交时，常用的方法是：证明直线和平面有且只有一个公共点；反证法；转化为平面问题.