第一章直角三角形的边角关系复习

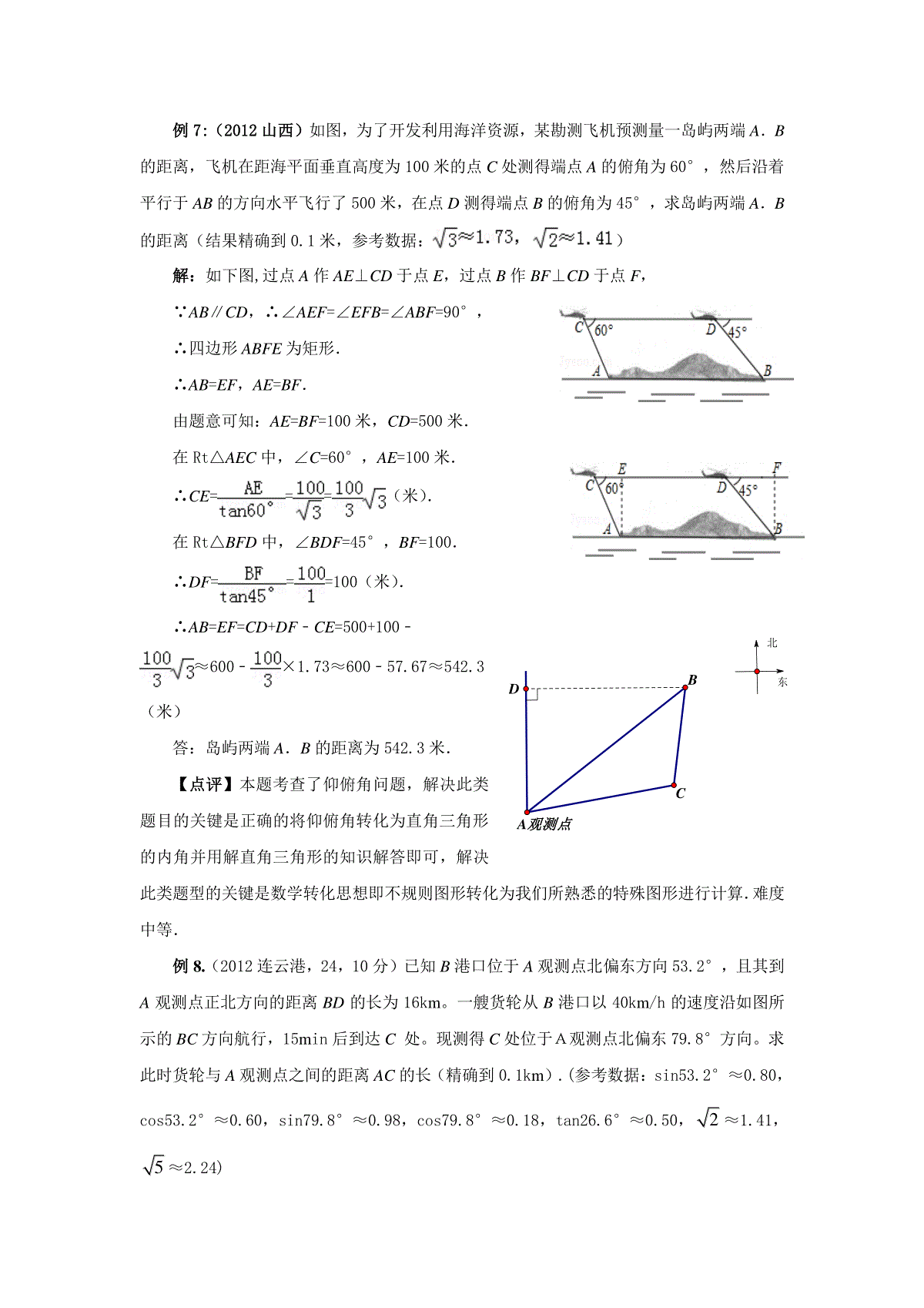
课时课题：第一章直角三角形的边角关系复习执教者：课型：复习课授课时间：2012年12月11日星期二第2节课教学目标：1．理解锐角三角函数的概念；2．会计算含30°，45°，60°角的三角函数值的问题.3．能够运用三角函数解直角三角形，并解决与直角三角形有关的实际问题.4.体会数形之间的联系，逐步学习利用数形结合的思想分析问题和解决问题.教学重点与难点：重点：能够运用三角函数解直角三角形，并解决与直角三角形有关的实际问题．难点：利用数形结合的思想分析问题和解决问题.教法及学法指导：小组交流互动课前准备：多媒体课件教学过程:一．考点解析考点一．锐角三角函数的概念如图，在△ABC中，∠C=90°(1)锐角A的对边与斜边的比叫做∠A的正弦，记为sinA，即ABBCAAsin斜边的对边(2)锐角A的邻边与斜边的比叫做∠A的余弦，记为cosA，即ABACAAcos斜边的邻边(3)锐角A的对边与邻边的比叫做∠A的正切，记为tanA，即ACBCAAAtan的邻边的对边BACECDABF例1：（2012连云港，）小明在学习“锐角三角函数”中发现，将如图所示的矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点E处，还原后，再沿过点E的直线折叠，使点A落在BC上的点F处，这样就可以求出67.5°的角的正切值是（）A.3+1B.2+1C.2.5D.5【解析】注意折叠后两点对称，也就是说△ABE和△AEF都是等腰三角形。得到67.5°的角为∠FAB。【答案】设AB=x,则BE=x,在直角三角形ABE中，用勾股定理求出AE=EF=2x,于是BF=（2+1）x.在直角三角形ABF中，tan∠FAB=(21)BFxABx=2+1=tan67.5°.选B。【点评】根据折叠得到A、E关于折痕对称，从而根据轴对称的性质得到等腰三角形。求出两线段的长。考点二．特殊角的三角函数值根据正弦、余弦和正切的定义，可以得到如下几个常用的特殊角的正弦、余弦和正切值。例2:（2012，湖北孝感）计算：cos245°+tan30°·sin60°=_____________．【解析】分别把cos45°=22的值，tan30°=33的值，sin60°=32的值代入进行计算即可．答案=1。【点评】本题考查特殊角三角函数值的计算，特殊角三角函数值计算在中考中经常出现，题型以选择题、填空题为主．牢记特殊角的三角函数值是解题的关键．例3:（2011甘肃兰州）已知α是锐角，且sin(α+15°)=32，计算10184cos(3.14)tan3的值。【答案】由sin(α+15°)=32得α=45°,原式=222411332考点三．解直角三角形（重点）在直角三角形中，除直角的五个量中，若已知其中的两个量（其中至少有一条边），就可以求出另外三个未知量。在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为cba、、。（1）三边之间关系：222cba（2）锐角之间关系：∠A+∠B=90°（3）边角之间关系：BcaAcossin,,sincosBcbAbaAtan,（4）面积公式：)(2121为斜边上的高hchabSABC（5）同角的三角函数的关系:sinA2＋cosA2＝1;tanA＝AAcossin（6）互为余角的函数之间的关系sin(90°－A)＝cosA，cos(90°－A)＝sinA，tanA.tan(90°－A)＝1例4:（2012四川内江）如图1所示，△ABC的顶点是正方形网格的格点，则sinA的值为()A．12B．55C．1010D．255【解析】欲求sinA，需先寻找∠A所在的直角三角形，而图形中∠A所在的△ABC并不是直角三角形，所以需要作高．观察格点图形发现连接CD（如下图2所示），恰好可证得CD⊥AB，于是有sinA＝CDAC＝210＝55．例5:（2011湖北荆州，8，3分）在△ABC中，∠A＝120°，AB＝4，AC＝2，则Bsin的值是（）CBA图2DA．1475B．53C．721D．1421【解析】如图，作ABC,延长BA，过点C作BA的垂线,交BA的延长线于点D,120CAB,∴60CAD,∴322360sinACCD,122160cosACAD，∴5ABADBD∴7225322BDCDBC,∴1421723sinBCCDB,答案选D.例6:(2012重庆，20，6分)已知：如图，在Rt△ABC中，∠BAC=90°，点D在BC边上，且△ABD是等边三角形。若AB=2，求△ABC的周长。（结果保留根号）【解析】由△ABC是直角三角形和△ABD是等边三角形，可求出∠C=30°,利用三角函数可求出答案。【答案】∵△ABD是等边三角形∴∠B=60°∵∠BAC=90°∴∠C=30°∵sinC=BCAB∴BC=CABsin=4,∵cosC=BCAC∴AC=BC·cosC=23∴△ABC的周长是6+23考点四.利用锐角三角函数解决实际应用解直角三角形，可将某些实际问题中的数量关系归结为直角三角形中的元素（边、角）之间的关系.一般有以下几个步骤：1.审题：认真分析题意，根据题目中的已知条件，画出它的平面图，弄清已知和未知；2.明确题目中的一些名词、术语的汉语，如仰角、俯角、跨度、坡角、坡度及方向角；3.是直角三角形的，根据边角关系进行计算；若不是直角三角形，应大胆尝试添加辅助线，把它们分割成一些直角三角形和矩形，把实际问题转化为直角三角形进行解决；4.确定合适的边角关系，细心推理计算。120ABDC42东北DA观测点CB例7:（2012山西）如图，为了开发利用海洋资源，某勘测飞机预测量一岛屿两端A．B的距离，飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了500米，在点D测得端点B的俯角为45°，求岛屿两端A．B的距离（结果精确到0.1米，参考数据：）解：如下图,过点A作AE⊥CD于点E，过点B作BF⊥CD于点F，∵AB∥CD，∴∠AEF=∠EFB=∠ABF=90°，∴四边形ABFE为矩形．∴AB=EF，AE=BF．由题意可知：AE=BF=100米，CD=500米．在Rt△AEC中，∠C=60°，AE=100米．∴CE===（米）．在Rt△BFD中，∠BDF=45°，BF=100．∴DF===100（米）．∴AB=EF=CD+DF﹣CE=500+100﹣≈600﹣×1.73≈600﹣57.67≈542.3（米）答：岛屿两端A．B的距离为542.3米．【点评】本题考查了仰俯角问题，解决此类题目的关键是正确的将仰俯角转化为直角三角形的内角并用解直角三角形的知识解答即可，解决此类题型的关键是数学转化思想即不规则图形转化为我们所熟悉的特殊图形进行计算．难度中等．例8.（2012连云港，24，10分）已知B港口位于A观测点北偏东方向53.2°，且其到A观测点正北方向的距离BD的长为16km。一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行，15min后到达C处。现测得C处位于Ａ观测点北偏东79.8°方向。求此时货轮与A观测点之间的距离AC的长（精确到0.1km）.(参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin79.8°≈0.98，cos79.8°≈0.18，tan26.6°≈0.50，2≈1.41，5≈2.24)【解析】过点B作AC的垂线，把所求线段AC换为两线段的差。利用Rt△ABH和Rt△BCH求线段AH、CH的长，利用AH－CH确定AC的长。【解】BC=40×1560=10.在Rt△ADB中，sin∠DAB=DBAB,sin53.2°≈0.8。所以AB=DABDBsin≈1.60.8=20.如图，过点B作BH⊥AC，交AC的延长线于H。在Rt△AHB中，∠BAH=∠DAC－∠DAB=63.6°―37°=26.6°，tan∠BAH=BHAH,0.5=BHAH,AH=2BH.BH2＋CH2=AB2,BH2+(2BH)2=202,BH=45,,所以AH=85，在Rt△AHB中，BH2＋CH2=BC2，CH=2108025所以AC=AH―CH=85―25＝65≈13.4km.【点评】本题的关键是把方位角放到相应的直角三角形中，找到直角三角形利用三角函数求出线段的长。五,测量物体的高度1．测量底部可以到达的物体的高度（重点）简单的测倾器由度盘、铅锤和支杆组成。如图。例9：（2012湖北襄阳）在一次数学活动中，李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪，去测量学校内一座假山的高度CD．如图5，已知李明距假山的水平距离BD为12m，他的眼睛距地面的高度为1.6m，李明的视线经过量角器零刻度线OA和假山的最高点C，此时，铅垂线OE经过量角器的60°刻度线，则假山的高度为（）A．(43＋1.6)mB．(123＋1.6)mC．(42＋1.6)mD．43m【解析】如下图，过点A作AF⊥CD于F，则AF＝BD＝12m，FD＝AB＝1.6m．DA观测点CBH53.2°16km79.8°AOBEDCF再由OE∥CF可知∠C＝∠AOE＝60°．所以，在Rt△ACF中，CF＝tan60AF＝43，那么CD＝CF＋FD＝(43＋1.6)m．【答案】A【点评】通过作高将问题转化为解直角三角形问题是解答关键，其间需要具有良好的阅读理解能力，能将对应线段和角之间的关系理清．2．测量底部不可以到达的物体的高度提示：测量底部不可以到达的物体的高度，求解时常要解两个直角三角形。例10：（2012山东青岛）如图，某校教学楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，教学楼在建筑物的墙上留下高2米的影子CE；而当光线与地面夹角是45°时，教学楼顶A在地面上的影子F与墙角C有13米的距离（B、F、C在一条直线上）⑴求教学楼AB的高度；⑵学校要在A、E之间挂一些彩旗，请你求出A、E之间的距离（结果保留整数）.（参考数据：sin22°≈38，cos22°≈1516，tan22°≈25）【解析】（1）过点D作DM⊥AB，若假设AB=x米，可表示出AM、ME的长，然后在Rt△AEM中，利用22°正切建立关系式来解.（2）根据（1）求出ME的长，再Rt△AME中，可求得ＡＥ之间的距离.【答案】解：⑴过点E作EM⊥AB，垂足为M.设AB为x.Rt△ABF中，∠AFB=45°，∴BF=AB=x，∴BC=BF+FC=x+13在Rt△AEM中，∠AEM=22°，AM=AB-BM=AB-CE=x-2，∴tan22°=MEAM，52132xxx=12.即教学楼的高12m.⑵由（1）可得ME=BC=x+13=12+13=25.在Rt△AME中，cos22°=AEME，MPDCBA∴ＡＥ＝ＭＥｃｏｓ２２°≈161525≈２７．即ＡＥ之间的距离约为２７ｍ．【点评】本题考查的是解直角三角形的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．例12：（2012四川省资阳市）小强在教学楼的点P处观察对面的办公大楼．为了测量点P到对面办公大楼上部AD的距离，小强测得办公大楼顶部点A的仰角为45°，测得办公大楼底部点B的俯角为60°，已知办公大楼高46米，CD＝10米．求点P到AD的距离（用含根号的式子表示）．解：连结PA、PB，过点P作PM⊥AD于点M；延长BC，交PM于点N，则∠APM=45°，∠BPM=60°，NM=10米设PM=x米在Rt△PMA中，AM=PM×tan∠APM=xtan45°＝x（米在Rt△PNB中，BN=PN×tan∠BPM=(x－10)tan60°＝(x－10)3（米）由AM+BN=46米，得x+(x－10)3＝46解得，4610313x，∴点P到AD的距离为4610313米．（结果为1838米也可）【点评】本题综合考查了直角三角形中的三角函数、特殊角的三角函数值及构造出的方程思想.解决本题的关键是作垂线构造出直角三角形