2018年湖北省各地市中考《二次函数》压轴题精编（含答案解析）

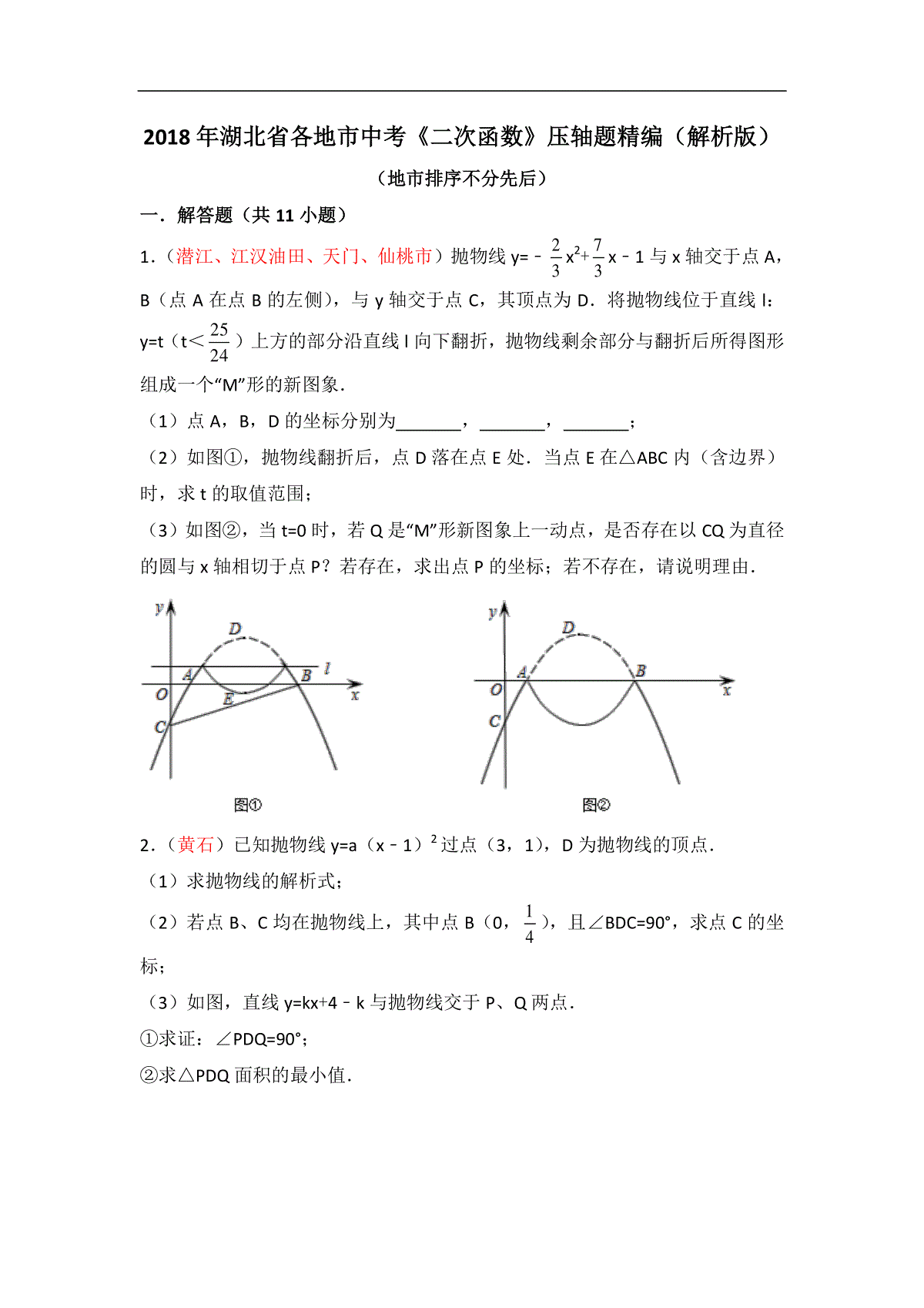
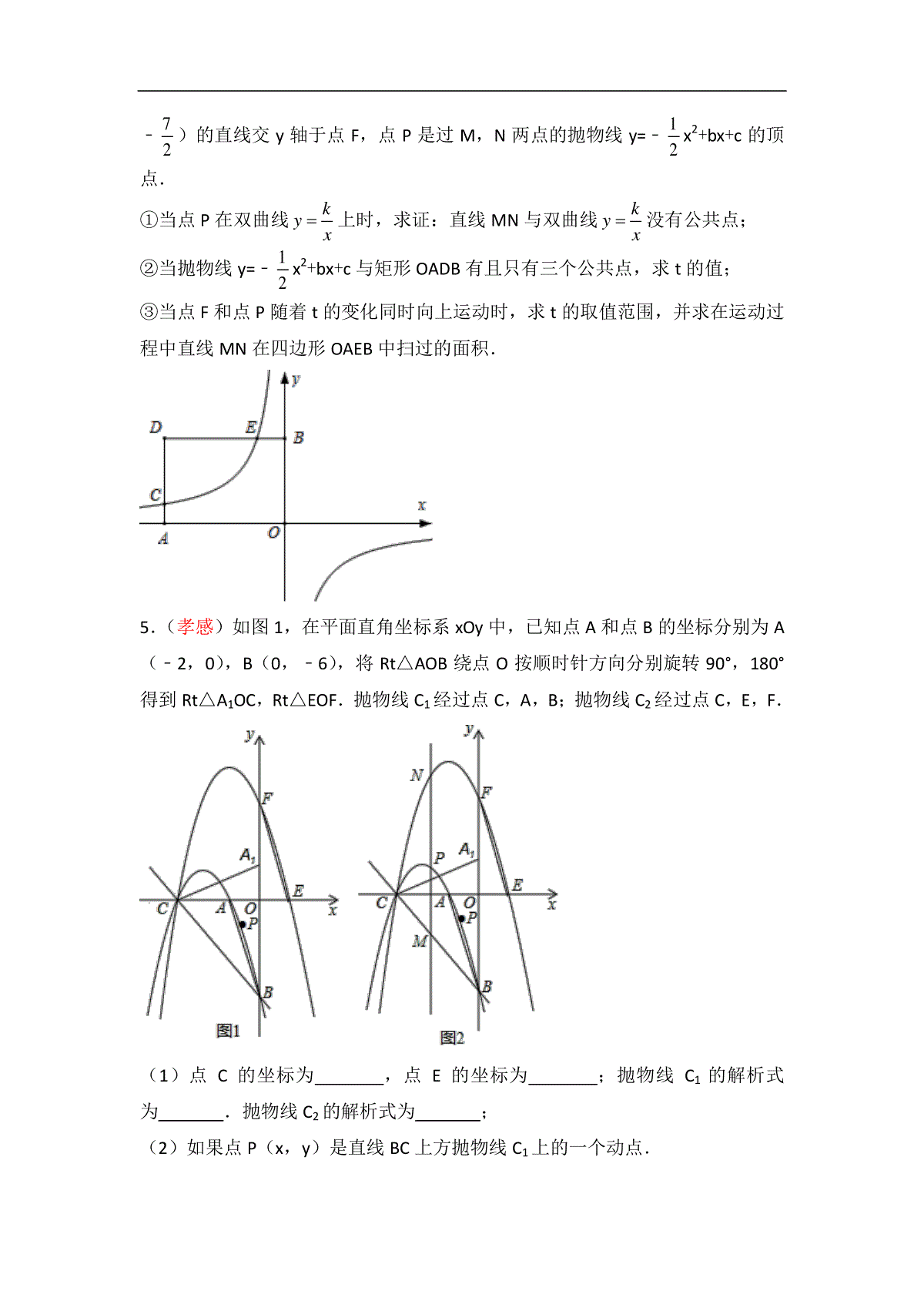
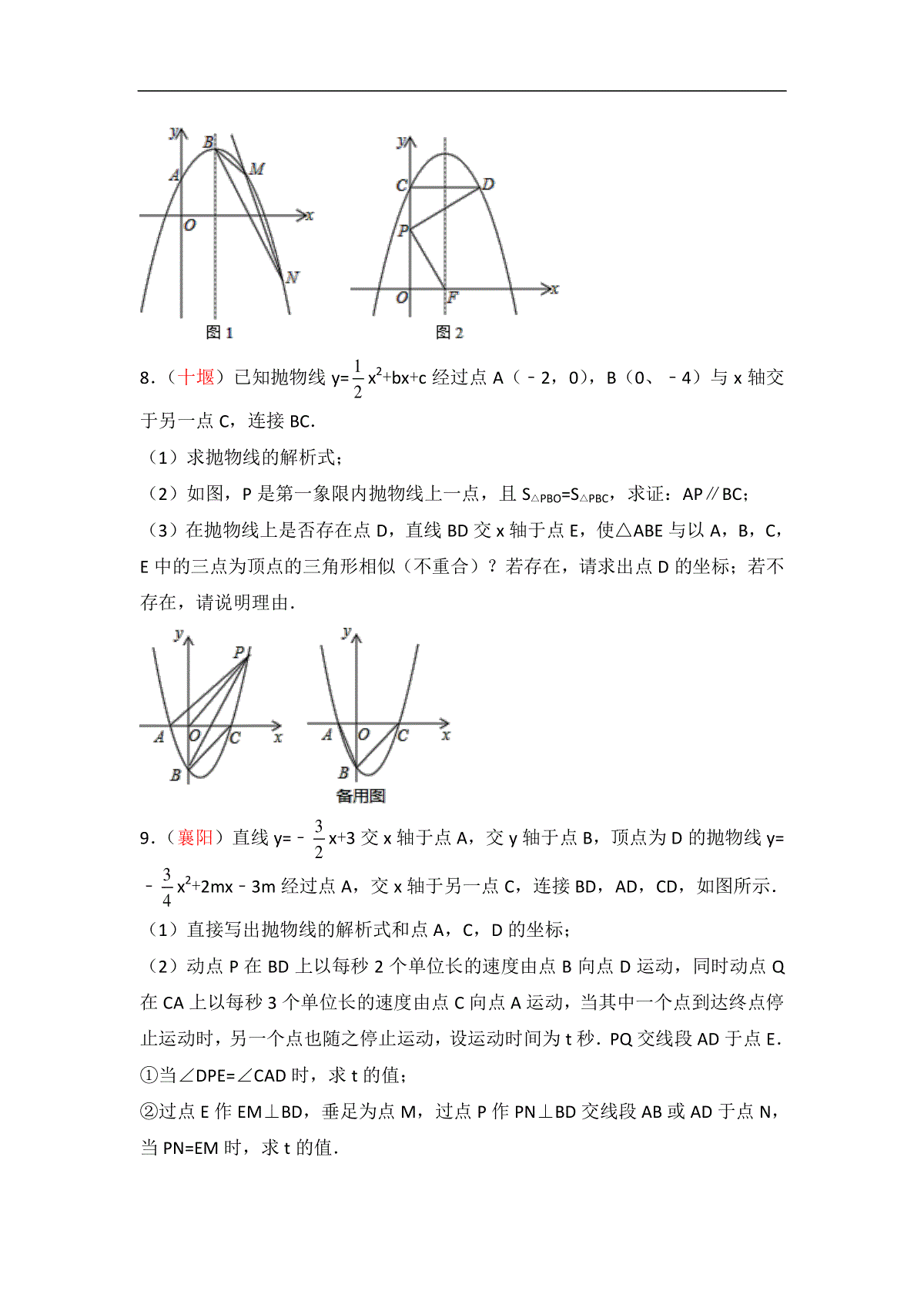
2018年湖北省各地市中考《二次函数》压轴题精编（解析版）（地市排序不分先后）一．解答题（共11小题）1．（潜江、江汉油田、天门、仙桃市）抛物线y=﹣23x2+73x﹣1与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，其顶点为D．将抛物线位于直线l：y=t（t＜2524）上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．（1）点A，B，D的坐标分别为，，；（2）如图①，抛物线翻折后，点D落在点E处．当点E在△ABC内（含边界）时，求t的取值范围；（3）如图②，当t=0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．2．（黄石）已知抛物线y=a（x﹣1）2过点（3，1），D为抛物线的顶点．（1）求抛物线的解析式；（2）若点B、C均在抛物线上，其中点B（0，14），且∠BDC=90°，求点C的坐标；（3）如图，直线y=kx+4﹣k与抛物线交于P、Q两点．①求证：∠PDQ=90°；②求△PDQ面积的最小值．3．（荆门）如图，抛物线y=ax2+bx+c（a≠0）与x轴交于原点及点A，且经过点B（4，8），对称轴为直线x=﹣2．（1）求抛物线的解析式；（2）设直线y=kx+4与抛物线两交点的横坐标分别为x1，x2（x1＜x2），当时，求k的值；（3）连接OB，点P为x轴下方抛物线上一动点，过点P作OB的平行线交直线AB于点Q，当S△POQ：S△BOQ=1：2时，求出点P的坐标．（坐标平面内两点M（x1，y1），N（x2，y2）之间的距离MN=）4．（宜昌）如图，在平面直角坐标系中，矩形OADB的顶点A，B的坐标分别为A（﹣6，0），B（0，4）．过点C（﹣6，1）的双曲线kyx（k≠0）与矩形OADB的边BD交于点E．（1）填空：OA=，k=，点E的坐标为；（2）当1≤t≤6时，经过点M（t﹣1，﹣12t2+5t﹣32）与点N（﹣t﹣3，﹣12t2+3t﹣72）的直线交y轴于点F，点P是过M，N两点的抛物线y=﹣12x2+bx+c的顶点．①当点P在双曲线kyx上时，求证：直线MN与双曲线kyx没有公共点；②当抛物线y=﹣12x2+bx+c与矩形OADB有且只有三个公共点，求t的值；③当点F和点P随着t的变化同时向上运动时，求t的取值范围，并求在运动过程中直线MN在四边形OAEB中扫过的面积．5．（孝感）如图1，在平面直角坐标系xOy中，已知点A和点B的坐标分别为A（﹣2，0），B（0，﹣6），将Rt△AOB绕点O按顺时针方向分别旋转90°，180°得到Rt△A1OC，Rt△EOF．抛物线C1经过点C，A，B；抛物线C2经过点C，E，F．（1）点C的坐标为，点E的坐标为；抛物线C1的解析式为．抛物线C2的解析式为；（2）如果点P（x，y）是直线BC上方抛物线C1上的一个动点．①若∠PCA=∠ABO时，求P点的坐标；②如图2，过点P作x轴的垂线交直线BC于点M，交抛物线C2于点N，记h=PM+NM+2BM，求h与x的函数关系式，当﹣5≤x≤﹣2时，求h的取值范围．6．（恩施州）如图，已知抛物线交x轴于A、B两点，交y轴于C点，A点坐标为（﹣1，0），OC=2，OB=3，点D为抛物线的顶点．（1）求抛物线的解析式；（2）P为坐标平面内一点，以B、C、D、P为顶点的四边形是平行四边形，求P点坐标；（3）若抛物线上有且仅有三个点M1、M2、M3使得△M1BC、△M2BC、△M3BC的面积均为定值S，求出定值S及M1、M2、M3这三个点的坐标．7．（武汉）抛物线L：y=﹣x2+bx+c经过点A（0，1），与它的对称轴直线x=1交于点B．（1）直接写出抛物线L的解析式；（2）如图1，过定点的直线y=kx﹣k+4（k＜0）与抛物线L交于点M、N．若△BMN的面积等于1，求k的值；（3）如图2，将抛物线L向上平移m（m＞0）个单位长度得到抛物线L1，抛物线L1与y轴交于点C，过点C作y轴的垂线交抛物线L1于另一点D．F为抛物线L1的对称轴与x轴的交点，P为线段OC上一点．若△PCD与△POF相似，并且符合条件的点P恰有2个，求m的值及相应点P的坐标．8．（十堰）已知抛物线y=12x2+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．（1）求抛物线的解析式；（2）如图，P是第一象限内抛物线上一点，且S△PBO=S△PBC，求证：AP∥BC；（3）在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．9．（襄阳）直线y=﹣32x+3交x轴于点A，交y轴于点B，顶点为D的抛物线y=﹣34x2+2mx﹣3m经过点A，交x轴于另一点C，连接BD，AD，CD，如图所示．（1）直接写出抛物线的解析式和点A，C，D的坐标；（2）动点P在BD上以每秒2个单位长的速度由点B向点D运动，同时动点Q在CA上以每秒3个单位长的速度由点C向点A运动，当其中一个点到达终点停止运动时，另一个点也随之停止运动，设运动时间为t秒．PQ交线段AD于点E．①当∠DPE=∠CAD时，求t的值；②过点E作EM⊥BD，垂足为点M，过点P作PN⊥BD交线段AB或AD于点N，当PN=EM时，求t的值．10．（随州）如图1，抛物线C1：y=ax2﹣2ax+c（a＜0）与x轴交于A、B两点，与y轴交于点C．已知点A的坐标为（﹣1，0），点O为坐标原点，OC=3OA，抛物线C1的顶点为G．（1）求出抛物线C1的解析式，并写出点G的坐标；（2）如图2，将抛物线C1向下平移k（k＞0）个单位，得到抛物线C2，设C2与x轴的交点为A′、B′，顶点为G′，当△A′B′G′是等边三角形时，求k的值：（3）在（2）的条件下，如图3，设点M为x轴正半轴上一动点，过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点，试探究在直线y=﹣1上是否存在点N，使得以P、Q、N为顶点的三角形与△AOQ全等，若存在，直接写出点M，N的坐标：若不存在，请说明理由．11．（咸宁）如图，直线y=﹣34x+3与x轴交于点A，与y轴交于点B．抛物线y=﹣38x2+bx+c经过A、B两点，与x轴的另一个交点为C．（1）求抛物线的解析式；（2）点P是第一象限抛物线上的点，连接OP交直线AB于点Q．设点P的横坐标为m，PQ与OQ的比值为y，求y与m的函数关系式，并求出PQ与OQ的比值的最大值；（3）点D是抛物线对称轴上的一动点，连接OD、CD，设△ODC外接圆的圆心为M，当sin∠ODC的值最大时，求点M的坐标．2018年湖北省各地市中考《二次函数》压轴题精编（解析）一．解答题（共11小题）1．（潜江、江汉油田、天门、仙桃市）抛物线y=﹣23x2+73x﹣1与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，其顶点为D．将抛物线位于直线l：y=t（t＜2524）上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．（1）点A，B，D的坐标分别为，，；（2）如图①，抛物线翻折后，点D落在点E处．当点E在△ABC内（含边界）时，求t的取值范围；（3）如图②，当t=0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．【学会思考】（1）利用二次函数图象上点的坐标特征可求出点A、B的坐标，再利用配方法即可找出抛物线的顶点D的坐标；（2）由点D的坐标结合对称找出点E的坐标，根据点B、C的坐标利用待定系数法可求出直线BC的解析式，再利用一次函数图象上点的坐标特征即可得出关于t的一元一次不等式组，解之即可得出t的取值范围；（3）假设存在，设点P的坐标为（12m，0），则点Q的横坐标为m，分m＜12或m＞3及12≤m≤3两种情况，利用勾股定理找出关于m的一元二次方程，解之即可得出m的值，进而可找出点P的坐标，此题得解．解：（1）当y=0时，有﹣23x2+73x﹣1=0，解得：x1=12，x2=3，∴点A的坐标为（12，0），点B的坐标为（3，0）．∵y=﹣23x2+73x﹣1=﹣23（x2﹣72x）﹣1=﹣23（x﹣74）2+2524，∴点D的坐标为（74，2524）．故答案为：（12，0）；（3，0）；（74，2524）．（2）∵点E、点D关于直线y=t对称，∴点E的坐标为（74，2t﹣2524）．当x=0时，y=﹣23x2+73x﹣1=﹣1，∴点C的坐标为（0，﹣1）．设线段BC所在直线的解析式为y=kx+b，将B（3，0）、C（0，﹣1）代入y=kx+b，，解得：，∴线段BC所在直线的解析式为y=13x﹣1．∵点E在△ABC内（含边界），∴，解得：516≤t≤2548．（3）当x＜12或x＞3时，y=﹣23x2+73x﹣1；当12≤x≤3时，y=23x2﹣73x+1．假设存在，设点P的坐标为（12m，0），则点Q的横坐标为m．①当m＜12或m＞3时，点Q的坐标为（m，﹣23x2+73x﹣1）（如图1），∵以CQ为直径的圆与x轴相切于点P，∴CP⊥PQ，∴CQ2=CP2+PQ2，即m2+（﹣23m2+73m）2=14m2+1+14m2+（﹣23m2+73m﹣1）2，整理，得：m1=142345，m2=142345，∴点P的坐标为（7345，0）或（7345，0）；②当12≤m≤3时，点Q的坐标为（m，23x2﹣73x+1）（如图2），∵以CQ为直径的圆与x轴相切于点P，∴CP⊥PQ，∴CQ2=CP2+PQ2，即m2+（23m2﹣73m+2）2=14m2+1+14m2+（23m2﹣73m+1）2，整理，得：11m2﹣28m+12=0，解得：m3=611，m4=2，∴点P的坐标为（311，0）或（1，0）．综上所述：存在以CQ为直径的圆与x轴相切于点P，点P的坐标为（7345，0）、（311，0）、（1，0）或（7345，0）．2．（黄石）已知抛物线y=a（x﹣1）2过点（3，1），D为抛物线的顶点．（1）求抛物线的解析式；（2）若点B、C均在抛物线上，其中点B（0，14），且∠BDC=90°，求点C的坐标；（3）如图，直线y=kx+4﹣k与抛物线交于P、Q两点．①求证：∠PDQ=90°；②求△PDQ面积的最小值．【学会思考】（1）将点（3，1）代入解析式求得a的值即可；（2）设点C的坐标为（x0，y0），其中y0=14（x0﹣1）2，作CF⊥x轴，证△BDO∽△DCF得=，即14==据此求得x0的值即可得；（3）①设点P的坐标为（x1，y1），点Q为（x2，y2），联立直线和抛物线解析式，化为关于x的方程可得，据此知（x1﹣1）（x2﹣1）=﹣16，由PM=y1=14（x1﹣1）2、QN=y2=14（x2﹣1）2、DM=|x1﹣1|=1﹣x1、DN=|x2﹣1|=x2﹣1知PM•QN=DM•DN=16，即=，从而得△PMD∽△DNQ，据此进一步求解可得；②过点D作x轴的垂线交直线PQ于点G，则DG=4，根据S△PDQ=12DG•MN列出关于k的等式求解可得．解：（1）将点（3，1）代入解析式，得：4a=1，解得：a=14，所以抛物线解析式为y=14（x﹣1）2；（2）由（1）知点D坐标为（1，0），设点C的坐标为（x0，y0），（x0＞1、y0＞0），则y0=14（x0﹣1）2，如图1，过点C作CF⊥x轴，∴∠BOD=∠DFC=90°、∠DCF+∠CDF=90°，∵∠BDC=90°，∴∠BDO+∠CDF=90°，∴∠BDO=∠DCF，∴△BDO∽△DCF，∴=，∴14==，解得：x0=17，此时y0=64，∴点C的坐标为（17，64）．（3）①证明：设点P的坐标为（x1，y1），点Q为（x2，y2），（其中x1＜1＜x2，y1＞0，y2＞0），由，得：x2﹣（4k+2）x+4k﹣15=0，∴，∴（x1﹣1）（x2﹣1）=﹣16，如图2，分别过点P、Q作x轴的垂线，垂足分别为M、N，则P