聊城市2017-2018学年八年级下期末考试数学试题(含答案解析)

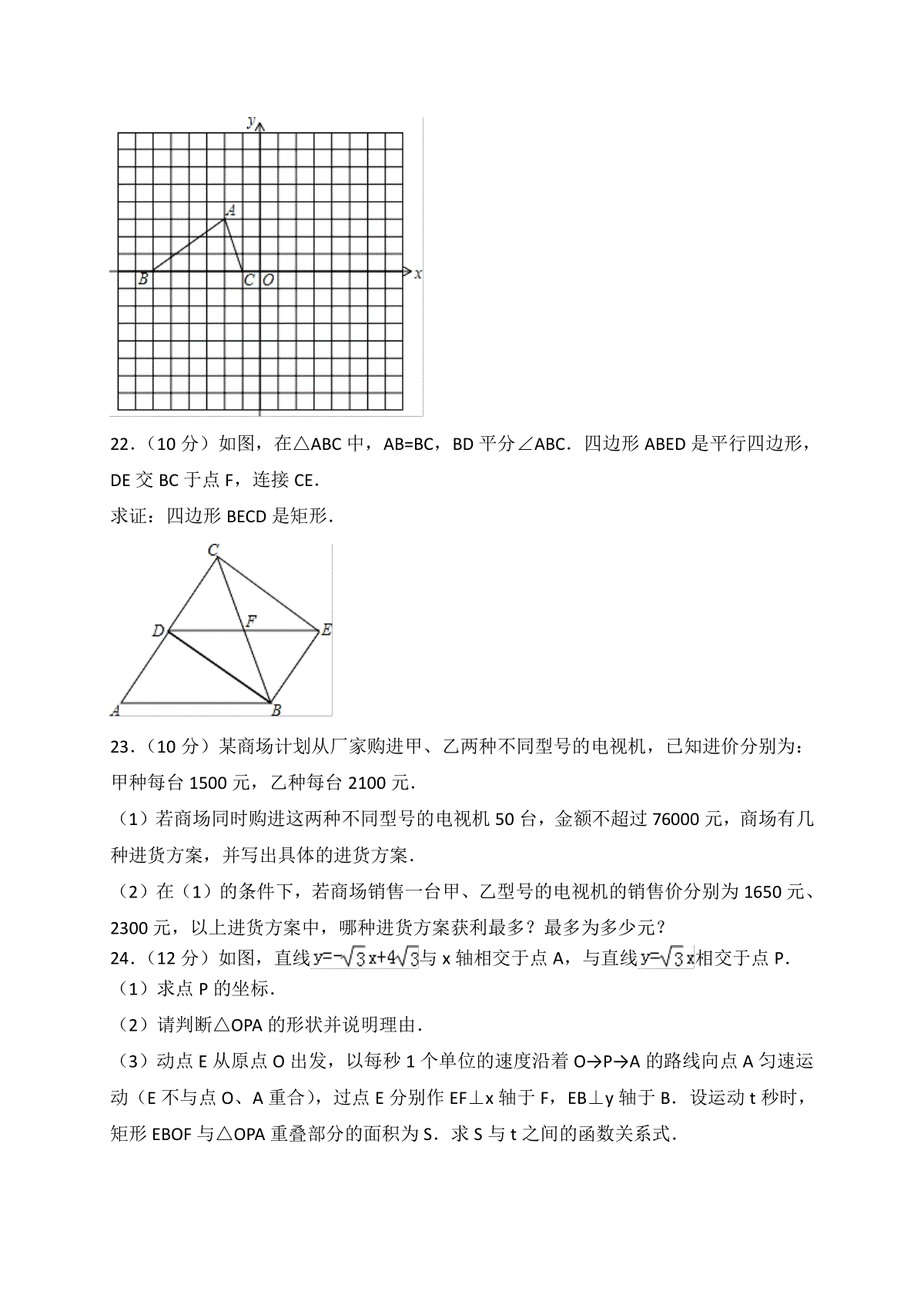
2017-2018学年山东省聊城市八年级（下）期末数学试卷一、选择题（本题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项符合题目要求1．如图图案中，不是中心对称图形的是（）2．如果不等式（a+1）x＜a+1的解集为x＞1，那么a的取值范围是（）A．a＜1B．a＜﹣1C．a＞1D．a＞﹣13．等式成立的条件是（）4．在实数范围内，下列判断正确的是（）A．若|m|=|n|，则m=nB．若a2＞b2，则a＞bC．若，则a=bD．若，则a=b5．如图，在矩形ABCD中，AB=8，BC=6，EF经过对角线的交点O，则图中阴影部分的面积是（）A．6B．12C．15D．246．若的值用a、b可以表示为（）7．如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（）A．1B．2C．3D．48．若不等式组的解集为﹣1＜x＜1，则（a﹣3）（b+3）的值为（）A．1B．﹣1C．2D．﹣29．以下是某市自来水价格调整表（部分）：（单位：元/立方米）用水类别现行水价拟调整水价一、居民生活用水0.721、一户一表第一阶梯：月用水量0～30立方米/户0.82第二阶梯：月用水量超过30立方米/户部分1.23则调整水价后某户居民月用水量x（立方米）与应交水费y（元）的函数图象是（）10．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD+PE的和最小值为（）11．如图，边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置，则图中阴影部分的面积为（）12．如图，两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是（）二、填空题（本题共6个小题，每小题4分，共24分，只要求写出最后结果13．m，n分别是﹣1的整数部分和小数部分，则2m﹣n=．14．若最简二次根式和是同类二次根式，则m=．15．点A（x1，y1）、B（x2，y2）在一次函数y=﹣2x+b的图象上，若x1＜x2，则y1y2（填“＜”或“＞”或“=”）．16．如图，一架云梯长10米，斜靠在一面墙上，梯子顶端离地面6米，要使梯子顶端离地面8米，则梯子的底部在水平面方向要向左滑动米．17．如图，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PB=2，则PP′=．18．如图，正方形ABCD的边长为1，以对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去第n个正方形的边长为．三、解咨题（本大题共6个小题共60分.解答要写出必要的文字说明、证明过程或演算步骤19．（8分）计算：20．（10分）解不等式组，并在数轴上把解集表示出来．21．（10分）如图所示，已知△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣6，0），C（﹣1，0）．（1）请直接写出点B关于点A对称的点的坐标；（2）将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．22．（10分）如图，在△ABC中，AB=BC，BD平分∠ABC．四边形ABED是平行四边形，DE交BC于点F，连接CE．求证：四边形BECD是矩形．23．（10分）某商场计划从厂家购进甲、乙两种不同型号的电视机，已知进价分别为：甲种每台1500元，乙种每台2100元．（1）若商场同时购进这两种不同型号的电视机50台，金额不超过76000元，商场有几种进货方案，并写出具体的进货方案．（2）在（1）的条件下，若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元，以上进货方案中，哪种进货方案获利最多？最多为多少元？24．（12分）如图，直线与x轴相交于点A，与直线相交于点P．（1）求点P的坐标．（2）请判断△OPA的形状并说明理由．（3）动点E从原点O出发，以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动（E不与点O、A重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B．设运动t秒时，矩形EBOF与△OPA重叠部分的面积为S．求S与t之间的函数关系式．2017-2018学年山东省聊城市八年级（下）期末数学试卷参考答案与试题解析一、选择题（本题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项符合题目要求1．如图图案中，不是中心对称图形的是（）A．B．C．D．【考点】R5：中心对称图形．【分析】根据中心对称图形的概念求解．【解答】解：A、是中心对称图形，故A选项错误；B、是中心对称图形，故B选项错误；C、是中心对称图形，故C选项错误；D、不是中心对称图形，故D选项正确；故选：D．2．如果不等式（a+1）x＜a+1的解集为x＞1，那么a的取值范围是（）A．a＜1B．a＜﹣1C．a＞1D．a＞﹣1【考点】C2：不等式的性质．【分析】根据不等式的基本性质进行计算即可．【解答】解：（a+1）x＜a+1，当a+1＜0时x＞1，所以a+1＜0，解得a＜﹣1，故选：B．3．等式=成立的条件是（）A．x＞B．x≥C．x＞2D．≤x＜2【考点】75：二次根式的乘除法．【分析】直接利用二次根式的性质得出关于x的不等式进而求出答案．【解答】解：∵等式=成立，∴，解得：x＞2．故选：C．4．在实数范围内，下列判断正确的是（）A．若|m|=|n|，则m=nB．若a2＞b2，则a＞bC．若=（）2，则a=bD．若=，则a=b【考点】27：实数．【分析】A、根据绝对值的性质即可判定；B、根据平方运算的法则即可判定；C、根据算术平方根的性质即可判定；D、根据立方根的定义即可解答．【解答】解：A、根据绝对值的性质可知：两个数的绝对值相等，则这两个数相等或互为相反数，故选项错误；B、平方大的，即这个数的绝对值大，不一定这个数大，如两个负数，故说法错误；C、两个数可能互为相反数，如a=﹣3，b=3，故选项错误；D、根据立方根的定义，显然这两个数相等，故选项正确．故选：D．5．如图，在矩形ABCD中，AB=8，BC=6，EF经过对角线的交点O，则图中阴影部分的面积是（）A．6B．12C．15D．24【考点】LB：矩形的性质．【分析】易证△AOE≌△COF，则阴影部分的面积为△CDO的面积，根据矩形对角线分成的四部分面积相等，即可计算阴影部分的面积，即可解题．【解答】解：在△AOE和△COF中，∠EAO=∠FCO，AO=CO，∠COF=∠EOA，∴△AOE≌△COF，则△AOE和△COF面积相等，∴阴影部分的面积与△CDO的面积相等，又∵矩形对角线将矩形分成面积相等的四部分，∴阴影部分的面积为=12．故选：B．6．若=a，=b，则的值用a、b可以表示为（）A．B．C．D．【考点】75：二次根式的乘除法．【分析】，化简即可．【解答】解：=．故选：C．7．如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（）A．1B．2C．3D．4【考点】KQ：勾股定理．【分析】根据直角三角形a、b、c为边，应用勾股定理，可得a2+b2=c2．（1）第一个图形中，首先根据等边三角形的面积的求法，表示出3个三角形的面积；然后根据a2+b2=c2，可得S1+S2=S3．（2）第二个图形中，首先根据圆的面积的求法，表示出3个半圆的面积；然后根据a2+b2=c2，可得S1+S2=S3．（3）第三个图形中，首先根据等腰直角三角形的面积的求法，表示出3个等腰直角三角形的面积；然后根据a2+b2=c2，可得S1+S2=S3．（4）第四个图形中，首先根据正方形的面积的求法，表示出3个正方形的面积；然后根据a2+b2=c2，可得S1+S2=S3．【解答】解：（1）S1=a2，S2=b2，S3=c2，∵a2+b2=c2，∴a2+b2=c2，∴S1+S2=S3．（2）S1=a2，S2=b2，S3=c2，∵a2+b2=c2，∴a2+b2=c2，∴S1+S2=S3．（3）S1=a2，S2=b2，S3=c2，∵a2+b2=c2，∴a2+b2=c2，∴S1+S2=S3．（4）S1=a2，S2=b2，S3=c2，∵a2+b2=c2，∴S1+S2=S3．综上，可得面积关系满足S1+S2=S3图形有4个．故选：D．8．若不等式组的解集为﹣1＜x＜1，则（a﹣3）（b+3）的值为（）A．1B．﹣1C．2D．﹣2【考点】CB：解一元一次不等式组．【分析】解不等式组后根据解集为﹣1＜x＜1可得关于a、b的方程组，解方程组求得a、b的值，代入代数式计算可得．【解答】解：解不等式2x﹣a＜1，得：x＜，解不等式x﹣2b＞3，得：x＞2b+3，∵不等式组的解集为﹣1＜x＜1，∴，解得：a=1，b=﹣2，当a=1，b=﹣2时，（a﹣3）（b+3）=﹣2×1=﹣2，故选：D．9．以下是某市自来水价格调整表（部分）：（单位：元/立方米）用水类别现行水价拟调整水价一、居民生活用水0.721、一户一表第一阶梯：月用水量0～30立方米/户0.82第二阶梯：月用水量超过30立方米/户部分1.23则调整水价后某户居民月用水量x（立方米）与应交水费y（元）的函数图象是（）A．B．C．D．【考点】E6：函数的图象．【分析】根据水费等于单价乘用水量，30立方米内单价低，水费增长的慢，超过30立方米的部分水费单价高，水费增长快，可得答案．【解答】解：30立方米内每立方是0.82元，超过30立方米的部分每立方是1.23元，调整水价后某户居民月用水量x（立方米）与应交水费y（元）的函数图象先增长慢，后增长快，B符合题意，故选：B．10．如图，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD+PE的和最小值为（）A．B．4C．3D．【考点】LE：正方形的性质；PA：轴对称﹣最短路线问题．【分析】由于点B与D关于AC对称，所以连接BE，与AC的交点即为P点．此时PD+PE=BE最小，而BE是等边△ABE的边，BE=AB，由正方形ABCD的面积为16，可求出AB的长，从而得出结果．【解答】解：设BE与AC交于点P'，连接BD．∵点B与D关于AC对称，∴P'D=P'B，∴P'D+P'E=P'B+P'E=BE最小．∵正方形ABCD的面积为16，∴AB=4，又∵△ABE是等边三角形，∴BE=AB=4．故选：B．11．如图，边长为1的正方形ABCD绕点A顺时针旋转30°到AB′C′D′的位置，则图中阴影部分的面积为（）A．B．C．1﹣D．1﹣【考点】R2：旋转的性质．【分析】设D′C′与BC的交点为E，连接AE，利用“HL”证明Rt△AD′E和Rt△ABE全等，根据全等三角形对应角相等∠BAE=∠D′AE，再根据旋转角求出∠BAD′=60°，然后求出∠BAE=30°，再解直角三角形求出BE，然后根据阴影部分的面积=正方形ABCD的面积﹣四边形ABED′的面积，列式计算即可得解．【解答】解：如图，D′C′与BC的交点为E，连接AE，在Rt△AD′E和Rt△ABE中，∵，∴Rt△AD′E≌Rt△ABE（HL），∴∠BAE=∠D′AE，∵旋转角为30°，∴∠BAD′=60°，∴∠BAE=×60°=30°，∴BE=1×=，∴阴影部分的面积=1×1﹣2×（×1×）=1﹣．故选：C．12．如图，两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是（）A．B．C．D．【考点】F3：一次函数的图象．【分析】根据一次函数的系数与图象的关系依次分析选项，找k、b取值范围相同的即得答案．【解答】解：根据一次函数的系数与图象的关系依次分析选项可得：A、由图可得，y1=kx+b中，k＜0，b＞0，y2=bx+k中，b＞0，k＜0，符合；B、由图可得，y1=kx+b中，k＞0，b＞0，y2=bx+k中，b＜0，k＞0，不符合；C、由图可得，y1=kx+b中，k＞0，b＜0，y2=bx+k中，b＜0