漯河市郾城区2015-2016学年八年级下期中数学试卷含答案解析

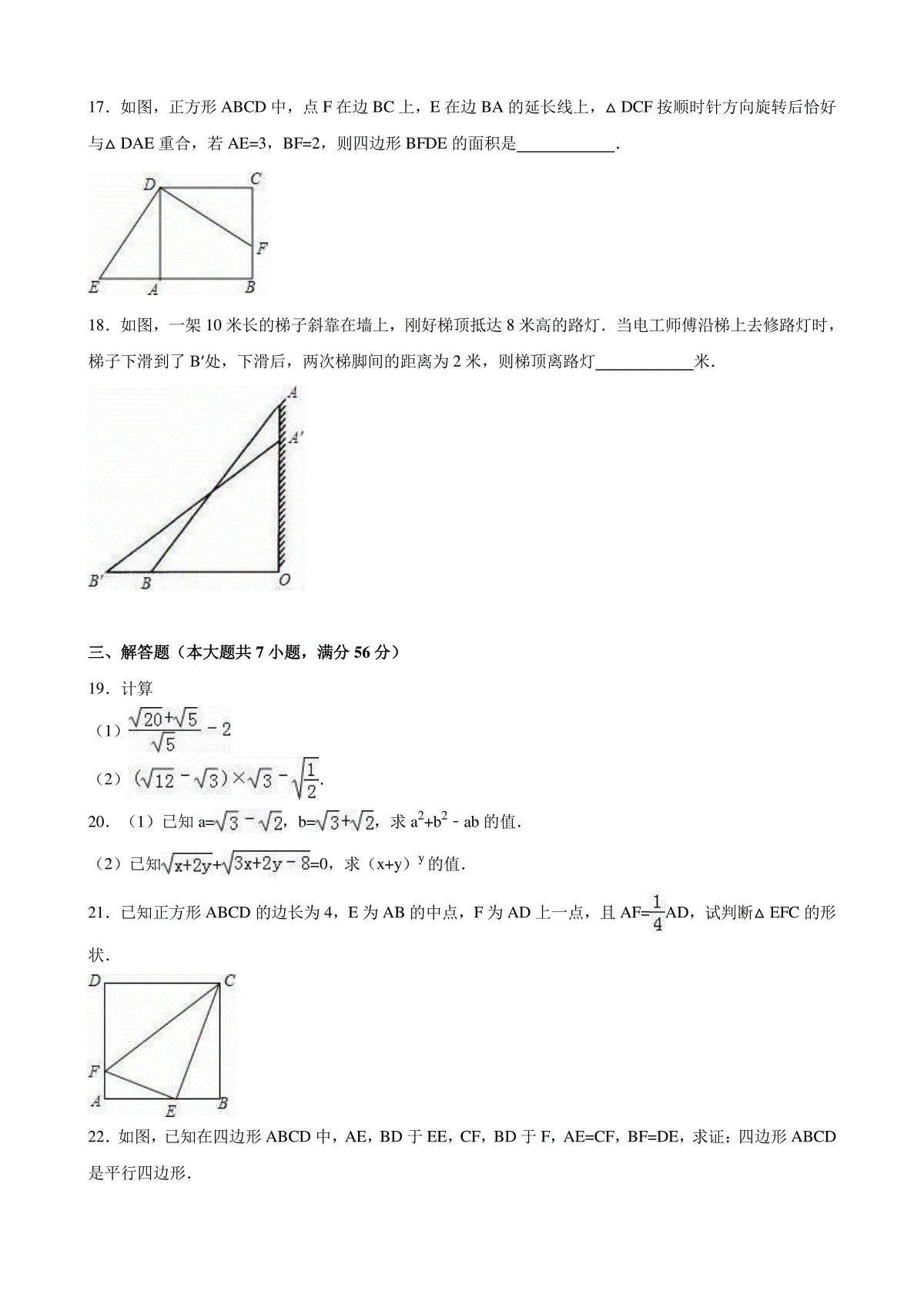
2015-2016学年河南省漯河市郾城区八年级（下）期中数学试卷一、选择题1．下列式子一定是二次根式的是（）A．B．C．D．2．在下列四组线段中，能组成直角三角形的是（）A．a=32，b=42，c=52B．a=11，b=12，c=13C．a=9，b=40，c=41D．a：b：c=1：1：23．下列二次根式中属于最简二次根式的是（）A．B．C．D．4．如图，在▱ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则线段BE、EC的长度分别为（）A．1和4B．4和1C．2和3D．3和25．顺次连结菱形四边中点所得的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形6．小明的作业本上有以下四题：①②③；④．做错的题是（）A．①B．②C．③D．④7．如图，直角三角形三边向形外作了三个正方形，其中数字表示该正方形的面积，那么正方形A的面积是（）A．360B．164C．400D．608．如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（）A．AB=DCB．∠1=∠2C．AB=ADD．∠D=∠B9．如图，在菱形ABCD中，M、N分别在AD、BC上，且AM=CN，MN与AC交于点O，连接DO，若∠BAC=28°，则∠ODC的度数为（）A．28°B．52°C．62°D．72°10．若有意义，则m能取的最小整数值是（）A．m=0B．m=1C．m=2D．m=3二、填空题11．①=；②=．12．平行四边形的周长为24，相邻两边长的比为3：1，那么这个平行四边形两邻边长分别为．13．若菱形的两条对角线长分别是6和8，则此菱形的周长是，面积是．14．当x=﹣1时，代数式x2+2x+2的值是．15．若直角三角形两直角边的比为3：4，斜边长为20，则此直角三角形的周长为．16．实数a、b在数轴上对应点的位置如图所示：则3a﹣=．17．如图，正方形ABCD中，点F在边BC上，E在边BA的延长线上，△DCF按顺时针方向旋转后恰好与△DAE重合，若AE=3，BF=2，则四边形BFDE的面积是．18．如图，一架10米长的梯子斜靠在墙上，刚好梯顶抵达8米高的路灯．当电工师傅沿梯上去修路灯时，梯子下滑到了B′处，下滑后，两次梯脚间的距离为2米，则梯顶离路灯米．三、解答题（本大题共7小题，满分56分）19．计算（1）（2）．20．（1）已知a=，b=，求a2+b2﹣ab的值．（2）已知+=0，求（x+y）y的值．21．已知正方形ABCD的边长为4，E为AB的中点，F为AD上一点，且AF=AD，试判断△EFC的形状．22．如图，已知在四边形ABCD中，AE，BD于EE，CF，BD于F，AE=CF，BF=DE，求证：四边形ABCD是平行四边形．23．已知，如图，折叠长方形的一边AD，使点D落在BC边上的点F处，如AB=8，BC=10．求EC的长．24．如图，在▱ABCD中，E，F分别为边AB，CD的中点，连接DE、BF、BD．（1）求证：△ADE≌△CBF．（2）若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．25．如图，菱形ABCD的边长为48cm，∠A=60°，动点P从点A出发，沿着线路AB﹣BD做匀速运动，动点Q从点D同时出发，沿着线路DC﹣CB﹣BA做匀速运动．（1）求BD的长；（2）已知动点P、Q运动的速度分别为8cm/s、10cm/s．经过12秒后，P、Q分别到达M、N两点，试判断△AMN的形状，并说明理由，同时求出△AMN的面积；（3）设问题（2）中的动点P、Q分别从M、N同时沿原路返回，动点P的速度不变，动点Q的速度改变为acm/s，经过3秒后，P、Q分别到达E、F两点，若△BEF为直角三角形，试求a的值．2015-2016学年河南省漯河市郾城区八年级（下）期中数学试卷参考答案与试题解析一、选择题1．下列式子一定是二次根式的是（）A．B．C．D．【考点】二次根式的定义．【分析】根据二次根式的概念“形如（a≥0）的式子，即为二次根式”，进行分析．【解答】解：根据二次根式的概念，知A、B、C中的被开方数都不会恒大于等于0，故错误；D、因为x2+2＞0，所以一定是二次根式，故正确．故选：D．【点评】此题考查了二次根式的概念，特别要注意a≥0的条件．2．在下列四组线段中，能组成直角三角形的是（）A．a=32，b=42，c=52B．a=11，b=12，c=13C．a=9，b=40，c=41D．a：b：c=1：1：2【考点】勾股定理的逆定理．【分析】欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．【解答】解：A、∵（32）2+（42）2≠（52）2，∴不能构成直角三角形，故本选项错误；B、∵112+122≠132，∴不能构成直角三角形，故本选项错误；C、∵92+402=412，∴能构成直角三角形，故本选项正确；D、∵12+12≠22，∴不能构成直角三角形，故本选项错误．故选C．【点评】本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．3．下列二次根式中属于最简二次根式的是（）A．B．C．D．【考点】最简二次根式．【分析】B、D选项的被开方数中含有未开尽方的因数或因式；C选项的被开方数中含有分母；因此这三个选项都不是最简二次根式．【解答】解：因为：B、=4；C、=；D、=2；所以这三项都不是最简二次根式．故选A．【点评】在判断最简二次根式的过程中要注意：（1）在二次根式的被开方数中，只要含有分数或小数，就不是最简二次根式；（2）在二次根式的被开方数中的每一个因式（或因数），如果幂的指数等于或大于2，也不是最简二次根式．4．如图，在▱ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则线段BE、EC的长度分别为（）A．1和4B．4和1C．2和3D．3和2【考点】平行四边形的性质．【分析】先根据角平分线及平行四边形的性质得出∠BAE=∠AEB，再由等角对等边得出BE=AB，从而求出EC的长．【解答】解：∵AE平分∠BAD交BC边于点E，∴∠BAE=∠EAD，∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC=5，∴∠DAE=∠AEB，∴∠BAE=∠AEB，∴AB=BE=3，∴EC=BC﹣BE=5﹣3=2．故选D．【点评】本题主要考查了角平分线、平行四边形的性质及等腰三角形的判定，根据已知得出∠BAE=∠AEB是解决问题的关键．5．顺次连结菱形四边中点所得的四边形一定是（）A．平行四边形B．矩形C．菱形D．正方形【考点】中点四边形．【分析】根据三角形的中位线定理首先可以证明：顺次连接四边形各边中点所得四边形是平行四边形．再根据对角线互相垂直，即可证明平行四边形的一个角是直角，则有一个角是直角的平行四边形是矩形．【解答】解：如图，四边形ABCD是菱形，且E、F、G、H分别是AB、BC、CD、AD的中点，则EH∥FG∥BD，EF=FG=BD；EF∥HG∥AC，EF=HG=AC，AC⊥BD．故四边形EFGH是平行四边形，又∵AC⊥BD，∴EH⊥EF，∠HEF=90°∴边形EFGH是矩形．故选：B．【点评】本题考查了中点四边形．能够根据三角形的中位线定理证明：顺次连接四边形各边中点所得四边形是平行四边形；顺次连接对角线互相垂直的四边形各边中点所得四边形是矩形；顺次连接对角线相等的四边形各边中点所得四边形是菱形．6．小明的作业本上有以下四题：①②③；④．做错的题是（）A．①B．②C．③D．④【考点】算术平方根．【分析】①②③④分别利用二次根式的性质及其运算法则计算即可判定．【解答】解：①和②是正确的；在③中，由式子可判断a＞0，从而③正确；在④中，左边两个不是同类二次根式，不能合并，故错误．故选D．【点评】此题主要考查了二次根式的性质及其简单的计算，注意二次公式的性质：=|a|．同时二次根式的加减运算实质上是合并同类二次根式．7．如图，直角三角形三边向形外作了三个正方形，其中数字表示该正方形的面积，那么正方形A的面积是（）A．360B．164C．400D．60【考点】勾股定理．【分析】要求正方形A的面积，则要知它的边长，而A正方形的边长是直角三角形的一直角边，利用另外两正方形的面积可求得该直角三角形的斜边和另一直角边，再用勾股定理可解．【解答】解：根据正方形的面积与边长的平方的关系得，图中直角三角形得A正方形的面积是1000﹣640=360，故选A．【点评】本题考查了直角三角形中勾股定理的运用，本题中根据勾股定理求斜边长的平方是解本题的关键．8．如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（）A．AB=DCB．∠1=∠2C．AB=ADD．∠D=∠B【考点】平行四边形的判定；平行线的判定与性质；三角形内角和定理；等腰梯形的性质．【分析】根据等腰梯形的定义判断A；根据平行线的性质可以判断B；根据平行四边形的判定可判断C；根据平行线的性质和三角形的内角和定理求出∠BAC=∠DCA，推出AB∥CD即可．【解答】解：A、符合条件AD∥BC，AB=DC，可能是等腰梯形，故A选项错误；B、根据∠1=∠2，推出AD∥BC，不能推出平行四边形，故B选项错误；C、根据AB=AD和AD∥BC不能推出平行四边形，故C选项错误；D、∵AD∥BC，∴∠1=∠2，∵∠B=∠D，∴∠BAC=∠DCA，∴AB∥CD，∴四边形ABCD是平行四边形，故D选项正确．故选：D．【点评】本题主要考查对平行四边形的判定，等腰梯形的性质，三角形的内角和定理，平行线的性质和判定等知识点的理解和掌握，能综合运用性质进行推理是解此题的关键．9．如图，在菱形ABCD中，M、N分别在AD、BC上，且AM=CN，MN与AC交于点O，连接DO，若∠BAC=28°，则∠ODC的度数为（）A．28°B．52°C．62°D．72°【考点】菱形的性质．【分析】首先由在菱形ABCD中，AM=CN，证得△AOM≌△CON（AAS），即可得O是对角线AC与BD的交点，继而求得答案．【解答】解：连接OD，∵四边形ABCD是菱形，∴AB∥CD，∴∠OAM=∠OCN，在△AOM和△CON中，，∴△AOM≌△CON（AAS），∴OA=OC，∴BD与AC相交于点O，∵∠ACD=∠BAC=28°，∴∠ODC=90°﹣∠ACD=62°．故选C．【点评】此题考查了菱形的性质以及全等三角形的判定与性质．注意证得BD与AC相交于点O是解此题的关键．10．若有意义，则m能取的最小整数值是（）A．m=0B．m=1C．m=2D．m=3【考点】二次根式有意义的条件．【分析】根据二次根式的性质，被开方数大于等于0，即可求解．【解答】解：由有意义，则满足3m﹣1≥0，解得m≥，即m≥时，二次根式有意义．则m能取的最小整数值是m=1．故选B．【点评】主要考查了二次根式的意义和性质．概念：式子（a≥0）叫二次根式；性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．二、填空题11．①=0.3；②=．【考点】二次根式的性质与化简．【分析】①先对根式下的数进行变形，（﹣0.3）2=（0.3）2，直接开方即得；，所以开方后||=．【解答】解：①原式=0.3；②原式=||=．【点评】本题考查的是对二次根式的化简和求值．12．平行四边形的周长为24，相邻两边长的比为3：1，那么这个平行四边形两邻边长分别为3cm和9cm．【考点】平行四边形的性质．【分析】根据平行四边形中对边相等和已知条件即可求得边长．【解答】解：如图∵平行四边形的周长为24cm∴AB+BC=24÷2=12∵BC：AB=3：1∴AB=3cm∴BC=9cm，故答案为：3cm和9cm．【点评】本题利用了平行四边形的对边相等的性质，设适当的参数建立方程求解．13．若菱形的两条对角线长分别是6和8，则此菱形的周长是20，面积是24．【考点】菱形的性质．【分析】首先根据题意画出图形，然后由菱形的两条对角线长分别是6和8，可求得OA=4，OB=3，再由勾股定理求得边长，继而求得此菱形的周长