当前位置:首页 > 中学教育 > 高中教育 > 第20讲 三角函数公式(解析版)
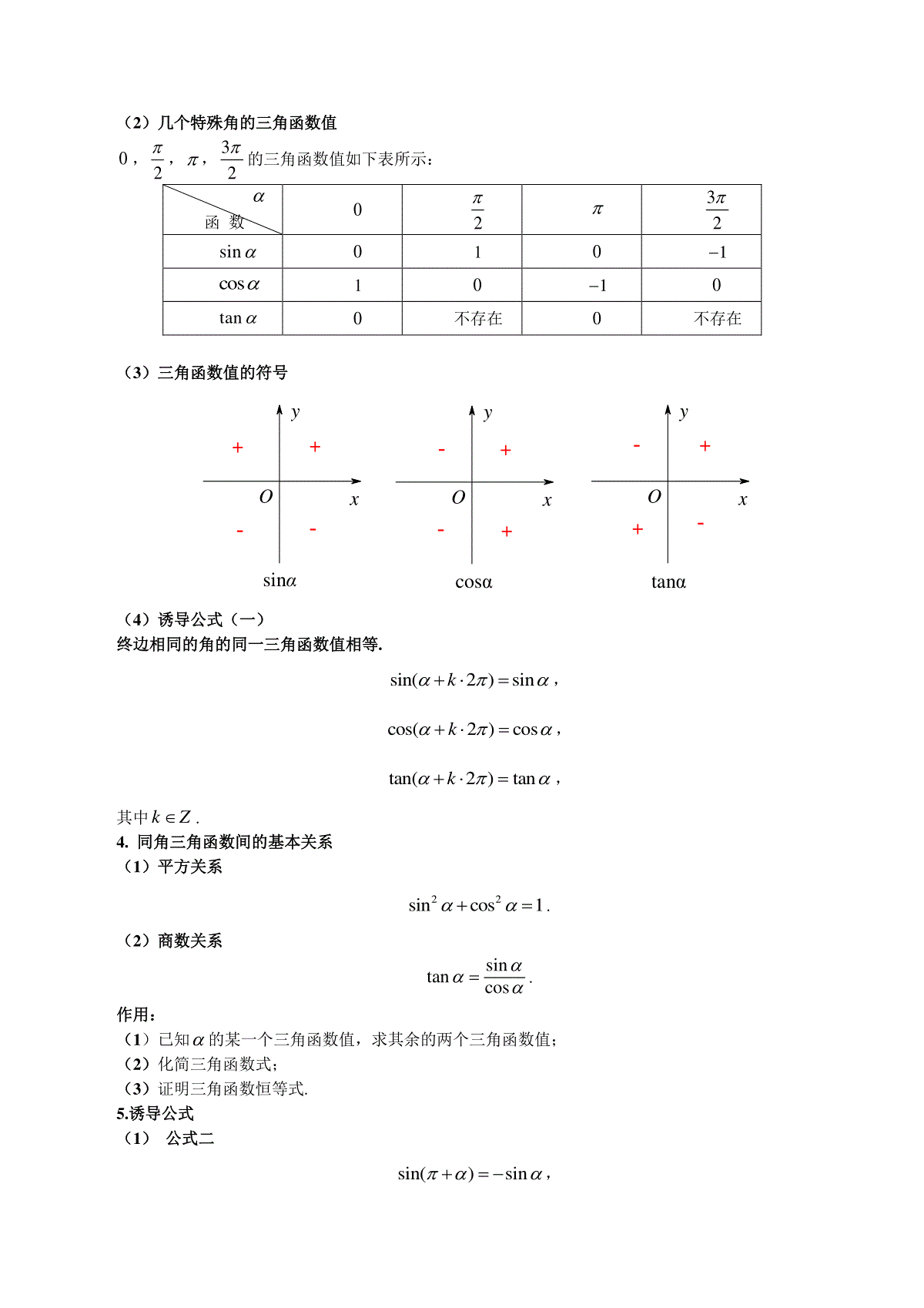
第20讲三角函数公式【知识点总结】1.任意角(1)角的概念角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.(2)正角、负角、零角按逆时针方向旋转所成的角叫正角;按顺时针方向旋转所成的角叫负角;一条射线没有作任何旋转而形成的角叫零角.(3)象限角当角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,那么角的终边(除端点外)在第几象限,就说这个角是第几象限角.如果角的终边落在坐标轴上,这时这个角不属于任何象限.(4)终边相同的角所有与角终边相同的角,连同角在内,可构成一个集合|360,SkkZ2.弧度制(1)弧度的概念长度等于半径长的圆弧所对的圆心角叫做1弧度的角.在半径为r的圆中,弧长为l的弧所对的圆心角为rad,那么lr.正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.(2)弧度与角度的换算(3)关于扇形的几个公式设扇形的圆心角为(rad),半径为R,弧长为l,则有①lR;②212SR;③12SlR.3.三角函数的概念(1)三角函数的定义已知角终边上的任一点(,)Pxy(非原点O),则P到原点O的距离220rOPxy.sin,cos,tanyxyrrx.1rad=180π()°≈57.3°1°=π180rad≈0.01745rad180°=πrad(2)几个特殊角的三角函数值0,2,,32的三角函数值如下表所示:函数0232sin0101cos1010tan0不存在0不存在(3)三角函数值的符号(4)诱导公式(一)终边相同的角的同一三角函数值相等.sin(2)sink,cos(2)cosk,tan(2)tank,其中kZ.4.同角三角函数间的基本关系(1)平方关系22sincos1.(2)商数关系sintancos.作用:(1)已知的某一个三角函数值,求其余的两个三角函数值;(2)化简三角函数式;(3)证明三角函数恒等式.5.诱导公式(1)公式二sin()sin,++++++tanαcosαsinαOxyOxyyxOcos()cos,tan()tan.(2)公式三sin()sin,cos()cos,tan()tan.(3)公式四sin()sin,cos()cos,tan()tan.(4)公式五sin()cos2,cos()sin2.(5)公式六sin()cos2,cos()sin2.6.常用三角恒等变形公式和角公式sin()sincossincoscos()coscossinsintantantan()1tantan差角公式sin()sincossincoscos()coscossinsintantantan()1tantan倍角公式sin22sincos2222cos2cossin2cos112sin22tantan21tan降次(幂)公式2211cos21cos2sincossin2;sin;cos;222半角公式1cos1cossin;cos;2222sin1costan.21cossina辅助角公式22sincossin(),tan(0),babababa角的终边过点(,)ab,特殊地,若22sincosabab或22ab,则tan.ba【典型例题】例1.(2022·全国·高三专题练习)已知圆锥的侧面积(单位:2cm)为2,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:2cm)是()A.2B.1C.12D.13【答案】B【详解】设圆锥底面半径为r,母线长为l,则21222rlrl,解得1,2rl.故选:B例2.(2022·全国·高三专题练习)已知角θ的顶点为坐标原点,始边为x轴的非负半轴,且cosθ=-35,若点M(x,8)是角θ终边上一点,则x等于()A.-12B.-10C.-8D.-6【答案】D【详解】角θ的顶点为坐标原点,始边为x轴的正半轴,且3cos5,若点M(x,8)是角θ终边上一点,则:x<0,利用三角函数的定义:2358xx,解得:x=-6.故选:D.例3.(2022·全国·高三专题练习)已知α,β∈5(,)36,若sin()6a=45,cos5()6=513,则sin(α-β)的值为()A.1665B.3365C.5665D.6365【答案】A【详解】由题意可得α+6∈(,)2,β-56∈(,0)2,所以cos()6a=-35,sin(β-56)=-1213,所以sin(α-β)=-sin[(α+6)-(β-56)]=-45312513513=1665.故选:A.(多选题)例4.(2022·全国·高三专题练习)已知5cos()5,5cos213,其中,为锐角,以下判断正确的是()A.sin21312B.19cos()565C.8coscos565D.11tantan8【答案】AC【详解】解:因为5cos()5,5cos213,其中,为锐角,所以:212sin21cos213,故A正确;因为25sin()5,所以cos()cos[2()]cos2cos()sin2sin()55122529()()513513565,故B错误;可得1152958coscos[cos()cos()]()52256565,故C正确;可得11295521sinsin[cos()cos()][()]52265565,所以21tantan8,故D错误.故选:AC.(多选题)例5.(2022·江苏·高三专题练习)下列说法正确的是()A.sin15cos152sin60B.()()()sin15sin15coscos15sinC.()coscoscossinsinD.()tantantan1tantan【答案】AB【详解】对于A,22sin15cos152sin15cos1522()2sin45152sin60,故A正确;对于B,由两角和的正弦公式,()()()sin15sin15coscos15sin,故B正确.对于C,()coscoscossinsin,故C错误.对于D,()tantantan1tantan,故D错误.故选:AB例6.(2022·全国·高三专题练习)已知α∈(0,2),β∈(﹣π,﹣2),sinα=7210,cosβ=255,则α+2β的值为______【答案】54【详解】因为α∈(0,2),β∈(﹣π,﹣2),sinα=7210,cosβ=255,所以2982cos1sin110010,2205sin1cos1255,所以sinsin1tan7,tancoscos2,所以22tan14tan211tan314,所以tantan2tan(2)1tantan247314173因为α∈(0,2),β∈(﹣π,﹣2),所以(2)2,2,所以524,故答案为:54例7.(2022·全国·高三专题练习)若0,2,4cos35,则sin___________【答案】34310【详解】0,2,5,336,43cos,sin3535,314343sinsinsincoscossin3333335252103故答案为:34310.例8.(2022·全国·高三专题练习)若tanα=2,则22sin1sin2的值为___________.【答案】134【详解】解析:法一:(切化弦的思想):因为tanα=2,所以sinα=2cosα,cosα=12sinα.又因为sin2α+cos2α=1,所以解得sin2α=45.所以224212sin12sin11354sin22sincos45.法二:(弦化切的思想)222222sin13sincos3tan132113sin22sincos2tan224.故答案为:134例9.(2022·全国·高三专题练习)已知πcos()4x=35,则sin2x=________.【答案】725【详解】∵sin2x=cos(2)2x=cos2()4x=2cos2()4x-1,∴sin2x=2×23()5-1=1825-1=725.故答案为:725【技能提升训练】一、单选题1.(2022·全国·高三专题练习)将手表的分针拨快10分钟,则分针在旋转过程中形成的角的弧度数是()A.6B.3C.6D.3【答案】D【分析】根据任意角的定义可得结果.【详解】将手表的分针拨快10分钟,则分针在旋转过程中形成的角的弧度数是102603.故选:D.2.(2022·全国·高三专题练习)与角2021终边相同的角是()A.221°B.2021C.221D.139【答案】A【分析】根据终边相同的角相差360的整数倍,逐个判断即可.【详解】2021360=5o余221,故A正确,B、C、D中的角均不与角2021终边相同.故选:A.【点睛】本题考查了终边相同角的概念,考查了简单的计算,属于概念题,本题属于基础题.3.(2022·全国·高三专题练习)与角94的终边相同的角的表达式中,正确的是()A.245k,kZB.93604k,kZC.360315k,kZD.54k,kZ【答案】C【分析】要写出与94的终边相同的角,只要在该角上加2的整数倍即可.【详解】首先角度制与弧度制不能混用,所以选项AB错误;又与94的终边相同的角可以写成92()4kkZ,所以C正确.故选:C.4.(2022·全国·高三专题练习)角的终边属于第一象限,那么3的终边不可能属于的象限是()A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【分析】由题意知,222kk,kZ,即可得3的范围,讨论3kn、31kn、32kn()nZ对应3的终边位置即可.【详解】∵角的终边在第一象限,∴222kk,kZ,则223363kk,kZ,当3()knnZ时,此时3的终边落在第一象限,当31()knnZ时,此时3的终边落在第二象限,当32()knnZ时,此时3的终边落在第三象限,综上,角的终边不可能落在第四象限,故选:D.5.(2022·全国·高三专题练习)若角的终边与240°角的终边相同,则角2的终边所在象限是()A.第二或第四象限B.第二或第三象限C.第一或第四象限D.第三或第四象限【答案】A【分析】写出的表达式,




 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:第20讲 三角函数公式(解析版)
链接地址:https://www.777doc.com/doc-12797001 .html