第三章清华大学数字图像处理课件

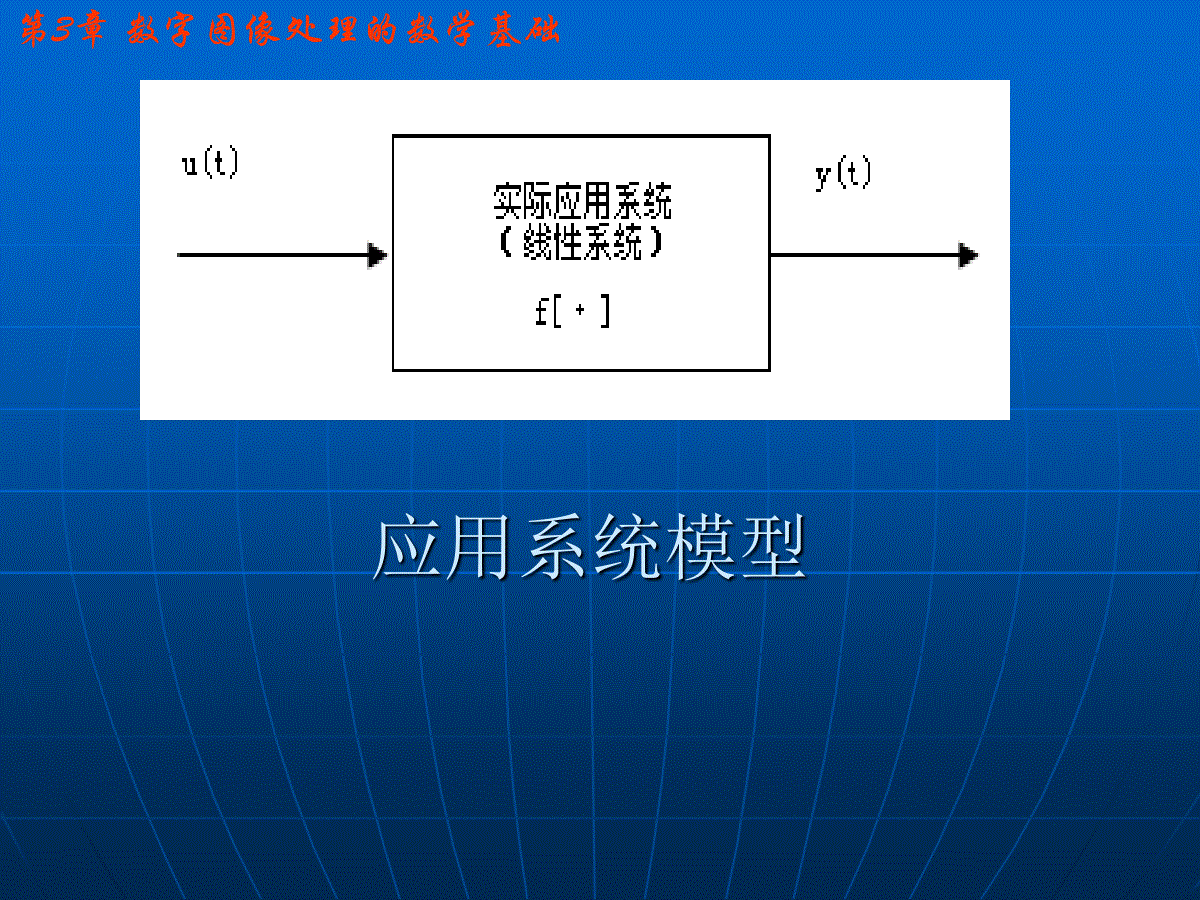
第3章数字图像处理的数学基础第三章数字图像处理的数学基础线性系统调谐信号分析卷积与滤波相关函数二维系统第3章数字图像处理的数学基础一、线性系统第3章数字图像处理的数学基础应用系统模型第3章数字图像处理的数学基础线性系统的特性：第3章数字图像处理的数学基础二、调谐信号分析第3章数字图像处理的数学基础第3章数字图像处理的数学基础第3章数字图像处理的数学基础3.系统的传递函数第3章数字图像处理的数学基础第3章数字图像处理的数学基础第3章数字图像处理的数学基础三、卷积与滤波1.连续卷积第3章数字图像处理的数学基础第3章数字图像处理的数学基础2.离散卷积jjihjuihiuiy)()()(*)()(第3章数字图像处理的数学基础3.滤波数学上的卷积运算在信号处理和图像处理学科上通常又称为滤波。线性移不变系统输入和输出之间的关系，除了可以用传递函数来描述之外，还可以采用卷积的方法来表示。即线性移不变系统的输出可通过输入信号与代表了系统特性的冲击响应函数h(t)的卷积得到。(滤波器的设计将在第6章详细讨论)第3章数字图像处理的数学基础其中h(t)与系统的冲激响应一致，因此称为冲击响应函数，即当输入为单位冲激函数时)(*)()()()()()(thtudtuhdthuty)()(*)()()()(ththtdthty第3章数字图像处理的数学基础三、相关函数1.相关函数的定义任意两个信号的相关函数定义：dthfthtftRfh)()()()()(相关函数是信号之间相似性的一种量度第3章数字图像处理的数学基础数学上可以证明，相关本质上是一个信号反折后的卷积2.相关函数与卷积的关系dthfthtftRfh)()()(*)()()(*)(thtf相关实质上也是一种滤波，因此，有些专著上将相关称为相关滤波。第3章数字图像处理的数学基础五.二维系统1二维线性系统设若该系统输入输出满足以下特性则称该二维系统为线性系统。)],([),(yxfTyxgii)],(),([),(),(22112211yxfayxfaTyxgayxga)],([)],([2211yxfTayxfTa第3章数字图像处理的数学基础2.二维位置不变线性系统对于任意一个二维系统，若给定输入f(x，y)，产生输出g(x，y)即：将输入信号自变量x和y分别平移x0和y0，若满足以下条件则称为二维位置不变线性系统)],([),(yxfTyxg)],([),(0000yyxxfTyyxxg第3章数字图像处理的数学基础3.二维系统的梯度算子(1)连续系统梯度算子对于连续系统，在坐标位置(x,y)处的梯度向量为：可写为：),(),(yxfyjyxfxiyfjxfi第3章数字图像处理的数学基础由于梯度是向量，因此其幅值为：梯度的方向为：22)()(yfxf)/arctan(xfyf第3章数字图像处理的数学基础(2)离散系统梯度算子在数字图像处理中，罗伯特算子、索贝尔算子、普瑞维特等各种梯度算子均以差分形式表示。)1,(),(),1(),(nmfnmffnmfnmffyx第3章数字图像处理的数学基础梯度的幅值为：为避免平方根运算，可以采用梯度近似值：22)()(fffyx第3章数字图像处理的数学基础为避免平方根运算，可以采用梯度近似值：①②离散系统梯度幅值与近似值关系：||||fffyx|)||,max(|fffyx||||)()(|)||,max(|22ffffffyxyxyx第3章数字图像处理的数学基础本章重点线性系统与调谐信号卷积与滤波二维位置不变系统