机械制图相贯线的画法

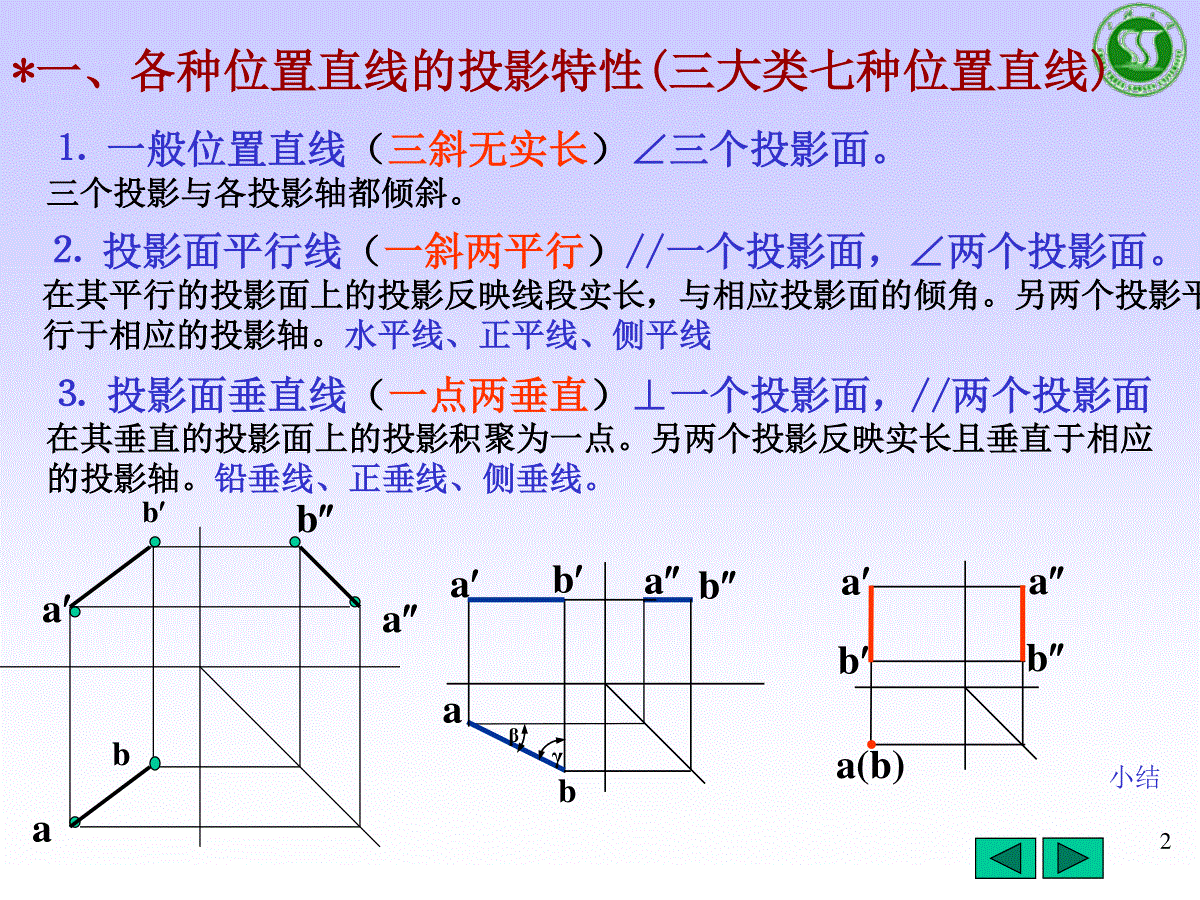
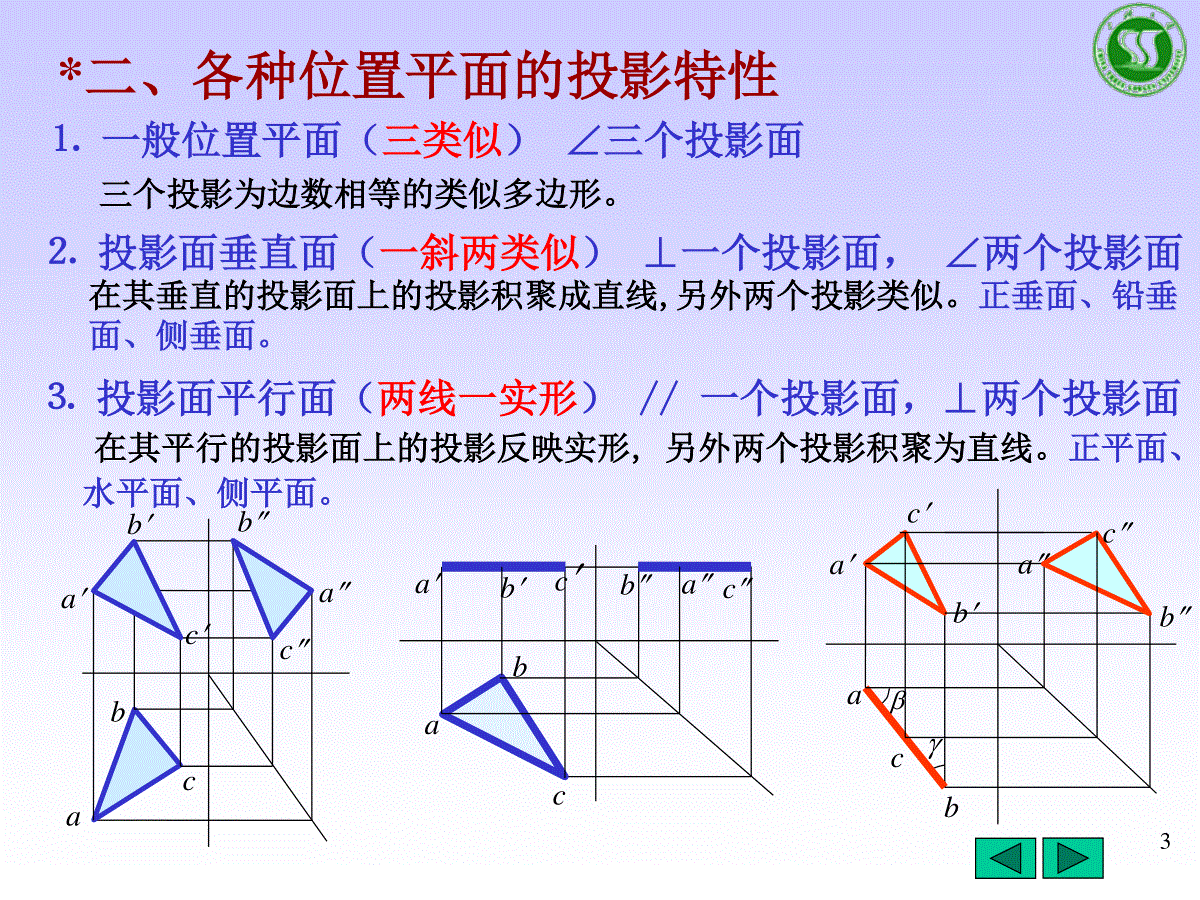
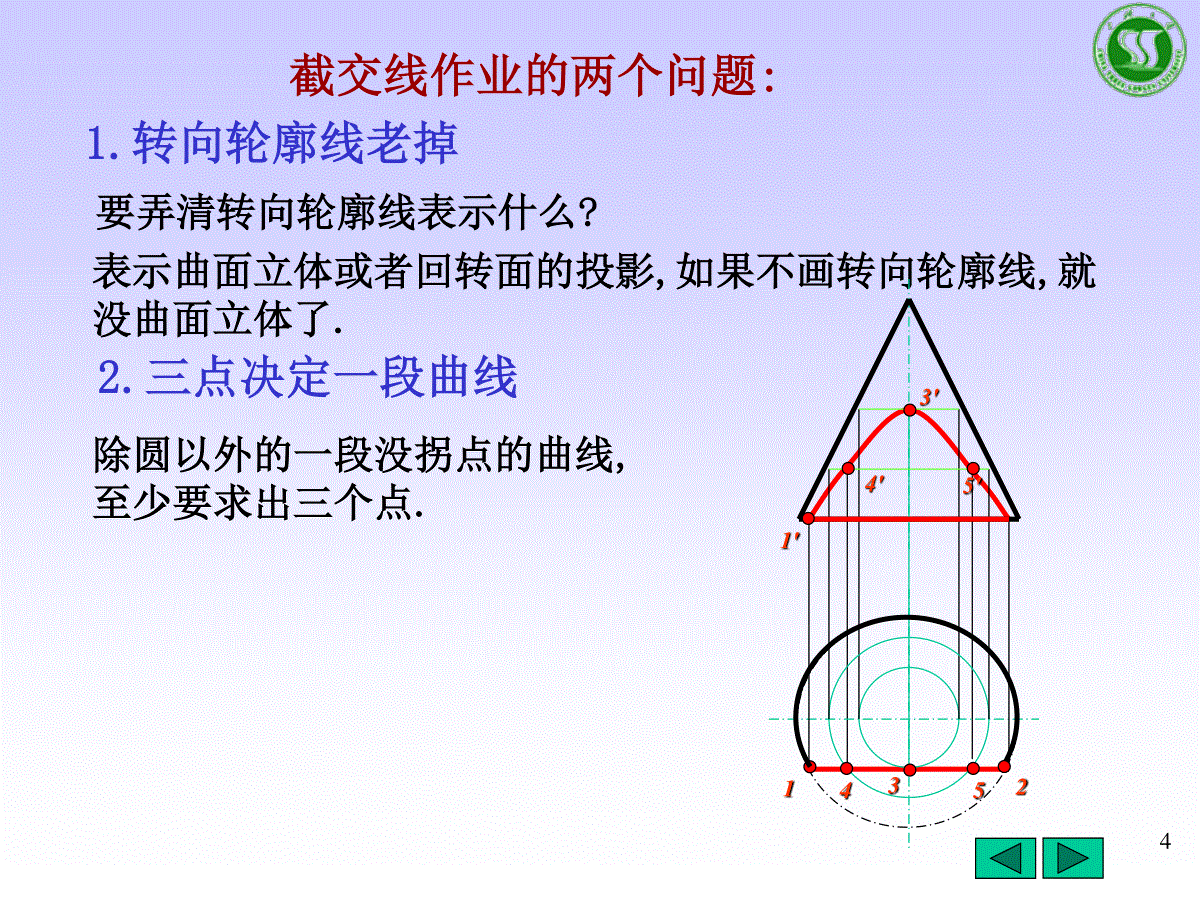
1P172小结*一、各种位置直线的投影特性(三大类七种位置直线)⒉投影面平行线（一斜两平行）//一个投影面，∠两个投影面。在其平行的投影面上的投影反映线段实长，与相应投影面的倾角。另两个投影平行于相应的投影轴。水平线、正平线、侧平线⒊投影面垂直线（一点两垂直）⊥一个投影面，//两个投影面在其垂直的投影面上的投影积聚为一点。另两个投影反映实长且垂直于相应的投影轴。铅垂线、正垂线、侧垂线。●aba(b)abbaaabbβγbaabba⒈一般位置直线（三斜无实长）∠三个投影面。三个投影与各投影轴都倾斜。3*二、各种位置平面的投影特性⒈一般位置平面（三类似）∠三个投影面⒉投影面垂直面（一斜两类似）⊥一个投影面，∠两个投影面⒊投影面平行面（两线一实形）//一个投影面，⊥两个投影面三个投影为边数相等的类似多边形。在其垂直的投影面上的投影积聚成直线,另外两个投影类似。正垂面、铅垂面、侧垂面。在其平行的投影面上的投影反映实形,另外两个投影积聚为直线。正平面、水平面、侧平面。ababbacccabbbaacccbbaaccbac4截交线作业的两个问题:1.转向轮廓线老掉要弄清转向轮廓线表示什么?表示曲面立体或者回转面的投影,如果不画转向轮廓线,就没曲面立体了.2.三点决定一段曲线除圆以外的一段没拐点的曲线,至少要求出三个点.33′454′5′121′5求截交线完全依赖立体形状不可取大多数情况下,由于空间形状千变万化,很难准确想出空间形状.这时结合线面分析法来求.线面分析法:即通过分析截平面和截交线上的特殊点和线的投影,来求截交线(在立体表面上)。用线面分析法要掌握以下五个要点:1.熟悉点（9个字）、线（三大类）、面（三大类）的投影特性；2.熟悉平面立体投影（棱柱.棱锥.棱台）、回转体的投影柱（两个矩形一个圆）、锥（两个三角形，一个圆）、球（三个圆）及其截交线（柱：三种，锥：五种，球：一种）的投影特性。3.熟悉平面立体（棱柱.棱锥.棱台）、和回转体（柱.锥2.球）表面上取点的方法。4.截交线都是用平面截出的，它的截交线应符合平面的投影特性。(一斜两类似，两线一实形)5.特殊点一定要先求出：转向轮廓线上的点，极限点(椭圆上短轴端点、抛物线和双曲线顶点，柱、锥底面的点)。另高平齐、长对正辅助线保留。以不变应万变6方法2.求各棱线与截平面的交点（即顶点)→棱线法。方法1.求各表面与截平面的交线(即多边形的边)→棱面法。关键是正确地画出截交线的投影。一般先用棱面法分析多边形有几个边，再用棱线法作图逐个求其顶点。213*三、平面立体切割的投影71）单个面截交线：求出截平面与各立体表面的交线（顶点为棱线或边的交点），即得截交线。2）多个平面截交线（切口和穿孔）：*截平面与各立体表面的截交线（在立体表面）*加上截平面之间的交线。顶点：是截平面与棱线的交点，加上相邻两截平面之间交线的端点（即交线与棱面的交点）。345617822133）注意：截平面之间的交线别掉了，并补齐棱线。8求回转体截交线的步骤（举例P16-4切球用投影分析作题）一）、空间及投影分析1.空间形状：柱3种，锥5种，球1种。2.投影分析：截平面与投影面的相对位置（一斜两类似、两线一实形）。二）、作图（高平齐、宽相等辅助线保留）1.逐个截平面求截交线（回转体表面上）：1）特殊点（控制截交线形状的极限点—最高、低、上、下、左、右，控制可见性和轮廓线的点—转向轮廓线上的点）；2）中间点；3）判断可见性，光滑连接。2.求截平面之间的交线。3.整理回转体轮廓线。加深顺序：粗实线d—虚线0.5d—点画线—细实线9习题P14102-4两回转体表面相交（相贯线）一、相贯线概述二、利用积聚性法求相贯线三、辅助平面法求相贯线四、相贯线的特殊情况五、组合相贯线六、小结11相贯线——立体相交后表面产生的交线。性质：(表面性、共有性、封闭性)１）．是相交两回转体表面的共有线。相贯线上的点是两回转体表面的共有点。２）．一般来说交线是一封闭的空间曲线，特殊情况下是平面曲线或直线。方法：相贯线→共有线→一系列共有点a).利用积聚性取点法b).辅助平面法一、相贯线的概述相贯线圆柱圆柱圆台圆柱相贯线12利用圆柱有一积聚性投影，相贯线与之重影，求得一个投影，再在另一回转体表面上取线、求点，即得相贯线的其他投影。二、利用积聚性取点法（表面取点法）求相贯线一)圆柱与圆柱的相贯线二)圆柱与圆锥、圆球的相贯线13例1.已知两圆柱的三面投影，求它们的相贯线。由于小圆柱轴线垂直于H面，相贯线的水平投影积聚其圆上。求正交两圆柱的相贯线？柱与柱——根据两圆柱面具有积聚性，得相贯线的两个投影，只需求另一投影（求一系列共有点）。大圆柱轴线垂直于W面，相贯线的W面投影在积聚圆上为圆弧，只有正面投影需要求。分析：由图知，直径不同的两圆柱轴线垂直相交，相贯线为前后左右对称的空间曲线。14求正交两圆柱的相贯线（1）求特殊点：作图步骤：13421’3’1”（3”）2”4”2’（4’）1.直接定出相贯线的最左点Ⅰ和最右点Ⅲ的三面投影。2.再求出出相贯线的最前点Ⅱ和最后点Ⅳ的三面投影。ⅠⅢⅡⅣ15求正交两圆柱的相贯线12341’2’1”（3”）2”4”2’（4’）3.求一般点：在已知相贯线的侧面投影图上任取5″、6″—5、6—5′、6′。5”6”565’（6’）4.判别可见性，光滑连接相贯线：相贯线的正面投影左右、前后对称，后面与前面的相贯线重影，只需按顺序光滑连接前面各点的投影。163.分析:当圆柱直径变化时，相贯线的变化趋势。交线从小圆柱向大圆柱轴线方向弯（小向大弯）直径相等为两条平面曲线（椭圆）垂直圆柱直径水平直径交线上下两条空间曲线垂直直径＞水平直径左右两条空间曲线174.立体表面相交有三种形式：一种是立体的两外表面相交;一种是外表面与内表面相交;一种是内表面与内表面相交.实实相贯实虚相贯虚虚相贯求柱与柱的相贯线，不管实虚，其求法一致，只是其可见性要根据情况正确判断处理。当两立体形状、大小和相对位置均相同，相贯线的形状也相同。注意点：相交处无转向轮廓线；孔的转向轮廓线为虚线184.圆柱相贯的四种形式:A(内外圆柱直径相等）19B：圆柱相贯（圆柱直径不等——水平柱垂直柱）20C：圆柱相贯（圆柱直径不等2——水平柱垂直柱）21D圆柱相贯（两外圆柱直径相等，内圆柱直径不等——水平垂直）22O5.圆柱与圆柱正交相贯线的近似画法相贯线朝向：总是从小圆柱向大圆柱轴线方向靠近。R为大圆柱半径23例2：补全主视图●●●●●1.两外表面相贯（直径相等）2.一内表面和一外表面相贯（直径不等）11’’2’’1’（2’）343’’（4’’）3’4’224无论是两外表面相交，还是一内表面和一外表面相交，或者两内表面相交，求相贯线的方法和思路是一样的。小结：252.可见性判别：当相贯线同时位于两立体表面的可见部分时才可见。#作业必p17.2-3,p18-3,选p17.5求相贯线时首先进行空间及投影分析，弄清相贯线是空间曲线还是平面曲线或直线，当相贯线的投影是非圆曲线时，一般按如下步骤：1．求特殊点:转向轮廓线上的点,相贯线的极限点(最高、低、前、后、左、右，椭圆长、短轴端点等);2．求中间点（在特殊点中间）;3．判别可见性，依次光滑连接各点;4．整理转向轮廓线和其他轮廓线。确定交线的范围确定交线的弯曲趋势1.作图步骤：#26例3．求空心圆柱与空心圆柱、空心圆柱与实心圆柱相交后的交线。(选讲)27例4求轴线交叉垂直圆柱相贯线的投影。(选讲)1“(2”)1'2'3’’123444'5”(6”)565'6'87yy8”(7”)8'7'3'28二)利用积聚性求相贯线（锥与球）也即已知锥（球）面上曲线的一个投影相贯线柱面上的曲线锥（球）面上的曲线已知相贯线的一个投影共有性求相贯线即转化为锥（球）面上求点、线。积聚性229301.求两曲面立体的相贯线，要求标注并求出所有的特殊点及两个一般点。1234561’3’4’5’6’2’7887相贯线是两立体的交线，即两立体表面的分界线，而曲面立体表面是用转向轮廓线表示的，所以曲面立体的转向线要补画到相贯线上的点。5’3’相贯线是锥面上的线，分解成一系列的点求其另一投影，作水平圆求点。作图:1）求特殊点2）求一般点3）判断可见性，依次光滑连接各点；4）补画转向轮廓线。31322.求两曲面立体的相贯线，要求标注并求出所有的特殊点。1’2’(3’)4’(5’)6’(7’)8’(9’)10’1107356289作图:1）求特殊点（前后锥面）：2）求一般点；3）判断可见性，依次光滑连接各点；4）补画H面投影转向轮廓线。4相贯线是两立体的交线，即两立体表面的分界线，而曲面立体表面是用转向轮廓线表示的，所以曲面立体的转向线要补画到相贯线上的点。3312双击进CAD#柱与锥1是最高点,2是最低点.341）求特殊点1.2.3.4.球面上的点。3’131”3”1’2）求一般点5.6.5”6”562”4”245’(6’)3）判断可见性(看W面)依次光滑连接各点.4）补画水平转向轮廓线。2’(4’)133.求两曲面立体的相贯线，要求标注并求出所有的特殊点及两个一般点。分析:相贯线的侧面投影积聚在圆柱的表面上。水平圆柱与半球的公共对称面平行于V面，故相贯线是一条前后对称的空间曲线。相贯线是球面上的线352345615’3’4’4.求两曲面立体的相贯线，要求标注并求出所有的特殊点及两个一般点。1）求特殊点1.2.3.4.5.6.2）求一般点：7.83）判断可见性，依次光滑连接各点：4）补画正面投影转向轮廓线。6’1’2’8’7’871’5’最高点和最低点?365.求柱与球的相贯线。（双击进autocad）376.求两曲面立体的相贯线。（双击进CAD）38圆柱与半球的相贯线辅助平面P辅助平面法：作一辅助平面P，使它与两回转体都相交，求出P平面与两回转体的截交线，而两回转体表面截交线的交点（三面共点），即为两回转体表面的共有点，亦即相贯线上的点。利用一系列辅助平面求出两回转体表面上的若干共有点，从而画出相贯线的投影。三、辅助平面法求相贯线39选辅助平面的原则：为了作图简单,要使辅助平面与两回转体表面交线的投影为直线或圆,常用的辅助平面为投影面的平行面或垂直面.40例1、求圆柱与半球相贯线的投影相贯线的侧面投影积聚在圆柱的表面上。水平圆柱与半球的公共对称面平行于V面，故相贯线是一条前后对称的空间曲线。1441作图步骤：1）求特殊点：4’141”4”1’2）求一般点：PvPw2”6”26QvQw3”5”352’(6’)3）判断可见性，依次光滑连接各点：4）补画水平转向轮廓线。3’(5’)Ⅰ14求圆柱与半球的相贯线42四、相贯线的特殊情况1.两回转体具有公共轴线时(过球心),其相贯线为垂直轴线的圆.43相贯线相贯线相贯线圆球与圆锥台相贯44相贯线的特殊情况2.两曲面立体相交，一般情况下相贯线为空间曲线，但特殊情况下可能是平面曲线或直线。A.当两回转体相交并公切于一球时，相贯线为平面曲线（椭圆）。B.当两圆锥共锥顶或者两圆柱轴线平行时，相贯线为直线。课作业P15-44546六、小结一、本节的基本内容⒈立体表面相贯线的概念⒉求相贯线的基本方法相贯线的性质：表面性共有性封闭性2）．辅助平面法：作辅助平面，截两回转体，得两截交线，其交线的交点即为所求相贯线上的点，作无数辅助平面，得无数点，连接即可。常用于：柱与球、柱与锥、锥与球，求相贯线。柱与柱：柱面上求线—已知两个投影—柱面求点。柱与锥：锥面上求线—已知一个投影—锥面求点(素线法和纬圆法)柱与球：球面上求线—已知一个投影—球面上求点(纬圆法)1）.积聚性取点法：利用圆柱有一积聚性投影，相贯线与之重影，求得一个投影，再在另一回转体表面上取线、求点，即得相贯线的其他投影。47二）、作图步骤：1．特殊点（最左、右、前、后、上、下、转向轮廓线上的点）；2．中间点（稀疏处，以便光滑连接曲线）；3．判别可见性，光滑连接；4．检查、加深。注意补齐转向线和轮廓线。二、解题过程