电工电子课程设计报告最新

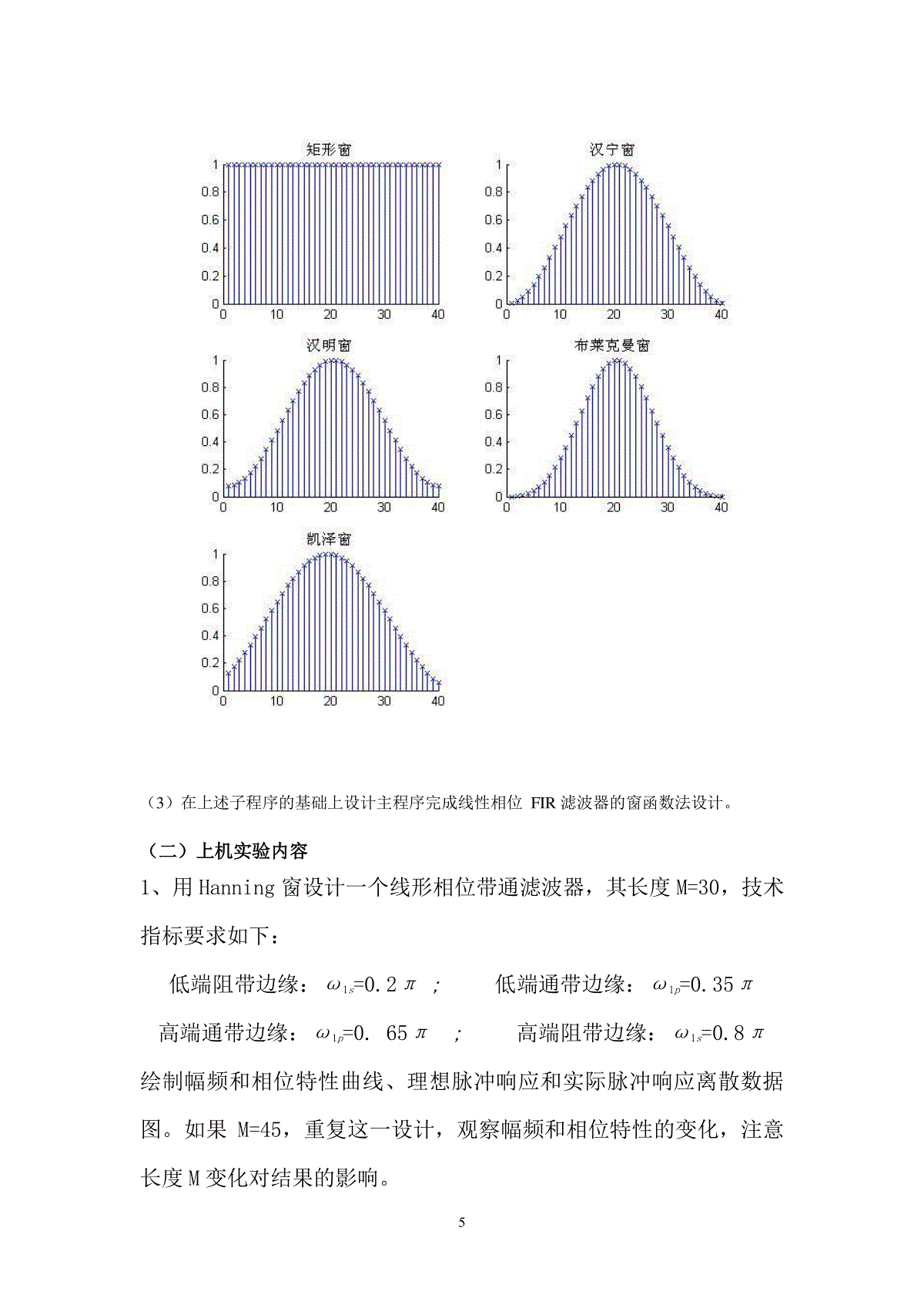
1电子系统课程设计报告FIR数字滤波器设计专业：07级电子信息工程班级：电信一班学号：XXXXXXX姓名：XXX指导老师：XXXXXXXXX同组成员：XXX时间：2010年7月1日2一、设计目的1、熟悉FIR滤波器设计的基本方法。2、掌握用窗函数设计FIR滤波器的基本原理和方法，熟悉MATLAB语言。3、熟悉线性相位FIR滤波器的幅频特性和相位特性。4、了解各种不同窗函数对滤波器性能的影响。5、熟悉MCS51系列单片机基本原理。6、掌握MCS51系列单片机基本指令和编程。7、利用MATLAB仿真的数据，用单片机实现FIR滤波器的设计。二、原理和方法（一）FIR滤波器的设计滤波器是设计来进行频率选择或频率分辨任务的线性时不变系统的通用名称。离散时间LTI(线性时不变)系统称为数字滤波器。按照LTI系统的单位脉冲响应长度是否有限可以分为有限长度脉冲响应(FIR)滤波器和无限长度脉冲响应(IIR)滤波器。FIR滤波器可以利用快速傅立叶变换进行快速卷积来实现，另外，FIR滤波器具有严格的相位特性，这对于语音信号处理和数据传输是很重要的。目前FIR滤波器的设计方法主要有三种：窗函数法、频率采样法和切比雪夫等波纹逼近的最优化设计方法。最常用的是窗函数法和切比雪夫等波纹逼近的最优化设计法。本设计中用的窗函数法比较简单，可以应用现成的窗函数公式，在技术要求不高的时候是比较方便灵活的。它从时域出发，用一个窗函数截取理想的hd(n)得到h(n)，以有限长序列h(n)近似理想的hd(n)；如果从频域出发，用理想的Hd(ejw)在单位圆上等角度取样得到h(k)，根据h(k)得到h(z)将逼近理想的hd(z)，这就是频率取样法。（二）窗函数法原理众所周知，数字滤波器的设计是基于一定的性能指标。窗函数法设计滤波器也不例外，首先要对滤波器提出性能指标。一般是给定一个理想的频率响应Hd(ejw)，使所设计的FIR滤波器的频率响应H(ejw)去逼近所要求的理想的滤波器的响应Hd(ejw)。窗函数法设计的任务在于寻找一个可实现（有限长单位脉冲响应）的传递函数：10)()(NnnjjenheH（4）去逼近Hd(ejw)。一般情况下，一个理想的频率响应Hd(ejw)的傅立叶反变换：deeHnhnjjdd)(21)(20（5）所得到的理想单位脉冲响应hd(n)是一个无限长序列。对hd(n)经过适当的加权、截断处理才能得到一个所需要的有限长脉冲响应序列。对应不同的加权、截断，就有不同的窗函数。而所要寻找的滤波器脉冲响应就等于理想脉冲响应和窗函数的乘积，即：)()()(nnhnhd（6）由此可见，窗函数的性质就决定了滤波器的品质。由于窗函数有一个等于M的有限长度，所以它的响应有一个主瓣，其宽度与1/M成正比，还有高度比较小的旁瓣。主瓣在Hd(ejw)中产生一个过渡带，主瓣的宽度决定过渡带的宽度，即与1/M成正比，主瓣越宽，则过渡带越宽，旁瓣产生波动。3以下是几种常用的窗函数：1、矩形窗101()()0MnMnRn，，其它（7）2、汉宁(Hanning)窗MnMnn1,12cos15.0)(（8）3、哈明(Hamming)窗)(12cos46.054.0)(nRMnnM（9）4、布莱克曼(Blackman)窗)(14cos08.012cos5.042.0)(nRMnMnnM（10）5、凯泽(Kaiser)窗10,11/21)(020MnIMnIn（11）其中I0[.]是修正过的零阶贝塞尔(Bessel)函数，β为依赖于M的参数，选择M可以产生各种过渡带宽和接近最优的阻带衰减。对于相同的M，凯泽窗可以提供不同的过渡带宽，这是其它窗所做不到的。窗函数法设计线性相位FIR滤波器可以按如下步骤进行：（1）确定数字滤波器的性能要求。确定各临界频率{ωk}和滤波器单位脉冲长度M。（2）根据性能要求和M值，合理地选择单位脉冲响应h(n)的奇偶对称性，从而确定理想频率响应Hd(ejw)的幅频特性和相位特性。（3）用傅立叶反变换公式（5）求得理想单位脉冲响应hd(n)。（4）选择适当的窗函数w(n)，根据式（6），求得所设计的FIR滤波器单位脉冲响应。（5）用傅立叶变换求得其频率响应H(ejw)，分析它的幅频特性，若不满足要求，可适当改变窗函数形式或长度M，重复上述过程，直到得到满意的结果。三、MATLAB实现的内容及步骤（一）编制实验用主程序及相应子程序1、在实验编程之前，认真复习有关FIR滤波器设计的有关知识，尤其是窗函数法的有关内容，阅读本实验原理与方法，熟悉窗函数及四种线形相位FIR滤波器的特性，掌握窗函数设计滤波器的具体步骤。2、编制窗函数设计FIR滤波器的主程序及相应子程序。（1）根据Hd(ejw)，利用傅立叶变换，编制产生理想单位脉冲响应hd(n)的简单子程序。（2）根据公式（7）到公式（10）编制相应的窗函数序列的子程序。41矩形窗程序：functionw=jvxing(x);M=x;forn=1:M;w(n)=1;end2汉宁窗程序：functionw=hn(x)M=xforn=1:Mw(n)=0.5*[1-cos(2*pi*n/(M+1))]end3汉明窗程序：functionw=hm(x);M=xforn=1:Mw(n)=0.54-0.46*cos(2*pi*(n-1)/(M-1))end4布莱克曼床程序：functionw=blkm(x);M=xforn=1:Mw(n)=0.42-0.5*cos(2*pi*(n-1)/(M-1))+0.08*cos((4*pi*(n-1)/(M-1)))end5凯泽窗程序：functionw=kz(x);M=x;beta=4（6，8）;forn=1:M;w(n)=besseli(0,(beta*sqrt(1-((2*n/(M-1))-1)^2)))/besseli(0,beta);end窗函数图形：5（3）在上述子程序的基础上设计主程序完成线性相位FIR滤波器的窗函数法设计。（二）上机实验内容1、用Hanning窗设计一个线形相位带通滤波器，其长度M=30，技术指标要求如下：低端阻带边缘：ω1s=0.2π;低端通带边缘：ω1p=0.35π高端通带边缘：ω1p=0.65π;高端阻带边缘：ω1s=0.8π绘制幅频和相位特性曲线、理想脉冲响应和实际脉冲响应离散数据图。如果M=45，重复这一设计，观察幅频和相位特性的变化，注意长度M变化对结果的影响。6主程序：Wp1=0.35*pi;Wp2=0.65*pi;Ws1=0.2*pi;Ws2=0.8*pi;M=30;N=M-1;M1=45;N1=M1-1;w=hn(M);%汉宁窗w1=hn(M1);Wc1=(Wp1+Ws1)/2;Wc2=(Wp2+Ws2)/2;k=0:N;k1=0:N1;hd=(Wc2/pi)*sinc(Wc2*(k-0.5*N)/pi)-(Wc1/pi)*sinc(Wc1*(k-0.5*N)/pi);hd1=(Wc2/pi)*sinc(Wc2*(k1-0.5*N1)/pi)-(Wc1/pi)*sinc(Wc1*(k1-0.5*N1)/pi);h=hd.*w;h1=hd1.*w1;omega=linspace(0,pi,512);mag=freqz(h,1,omega);magdb=20*log(abs(mag));mag1=freqz(h1,1,omega);magdb1=20*log(abs(mag1));subplot(321)plot(omega/pi,magdb,'-b',omega/pi,magdb1,'-r');title('幅频特性（加汉宁窗）')xlabel('normalizekfrequency(rad/s)*π');ylabel('Gain,dB');legend('M=30','M=45');grid;phase=unwrap(angle(mag));phase1=unwrap(angle(mag1));subplot(322);plot(omega,phase,'-b',omega,phase1,'-r');title('相位特性');xlabel('Normalizedfrequencyrad/s');ylabel('phaserad');legend('M=30','M=45');grid;subplot(323)stem(k,h);title('实际脉冲响应离散数据图M=30');grid;subplot(324)stem(k,hd);title('理想脉冲响应离散数据图M=30');grid;subplot(325)stem(k1,h1);title('实际脉冲响应离散数据图M=45');grid;subplot(326)7stem(k1,hd1);title('理想脉冲响应离散数据图M=45');grid;图形：分析：随着长度M的增加滤波器的过渡带减小，阻带特性变好，理想脉冲和实际脉冲幅度增大。82、改用矩形窗和Blackman窗，设计步骤（1）中的带通滤波器，观察并记录窗函数对滤波器幅频和相位特性的影响，比较这三种窗函数的特点。程序：Wp1=0.35*pi;Wp2=0.65*pi;Ws1=0.2*pi;Ws2=0.8*pi;N=45;M=N-1;w1=jvxing(N);w2=hn(N);w3=blkm(N);Wc1=(Wp1+Ws1)/2;Wc2=(Wp2+Ws2)/2;k=0:M;hd=(Wc2/pi)*sinc(Wc2*(k-0.5*M)/pi)-(Wc1/pi)*sinc(Wc1*(k-0.5*M)/pi);h1=hd.*w1;h2=hd.*w2;h3=hd.*w3;omega=linspace(0,pi,512);mag1=freqz(h1,1,omega);magdb1=20*log(abs(mag1));mag2=freqz(h2,1,omega);magdb2=20*log(abs(mag2));mag3=freqz(h3,1,omega);magdb3=20*log(abs(mag3));subplot(211)plot(omega/pi,magdb1,'b-',omega/pi,magdb2,'r-',omega/pi,magdb3,'g-');legend('矩形窗','汉纳窗','布莱克曼窗')title('幅频特性')xlabel('normalizekfrequency');ylabel('Gain,dB');grid;phase1=unwrap(angle(mag1));phase2=unwrap(angle(mag2));phase3=unwrap(angle(mag3));subplot(212)plot(omega,phase1,'b-',omega,phase2,'r-',omega,phase3,'g-');legend('矩形窗','汉纳窗','布莱克曼窗')title('相位特性');ylabel('phase');grid;图形：9分析：在长度相同（M=45）情况下，加矩形窗的滤波器过渡带要小于加布莱克曼窗，而加布莱克曼窗的阻带特性比加矩形窗好（衰减大），加汉纳窗则介于二者之间。相位特性：加矩形窗、汉纳窗、布莱克曼窗滤波器在通带相位特性良好（基本是直线）。103、用Kaiser窗设计一个专用的线性相位滤波器。M=40，理想幅频特性如下：其它,08.06.0,14.02.0,1|)(|jdeH当β值分别为4,6,8时，设计相应的滤波器，比较它们的幅频和相位特性，观察并分析β值不同的时候对结果有什么影响。主程序：M=40;Wc1=0.2*pi;Wc2=0.4*pi;Wc3=0.6*pi;Wc4=0.8*pi;w=kz(M)