结构力学复习2

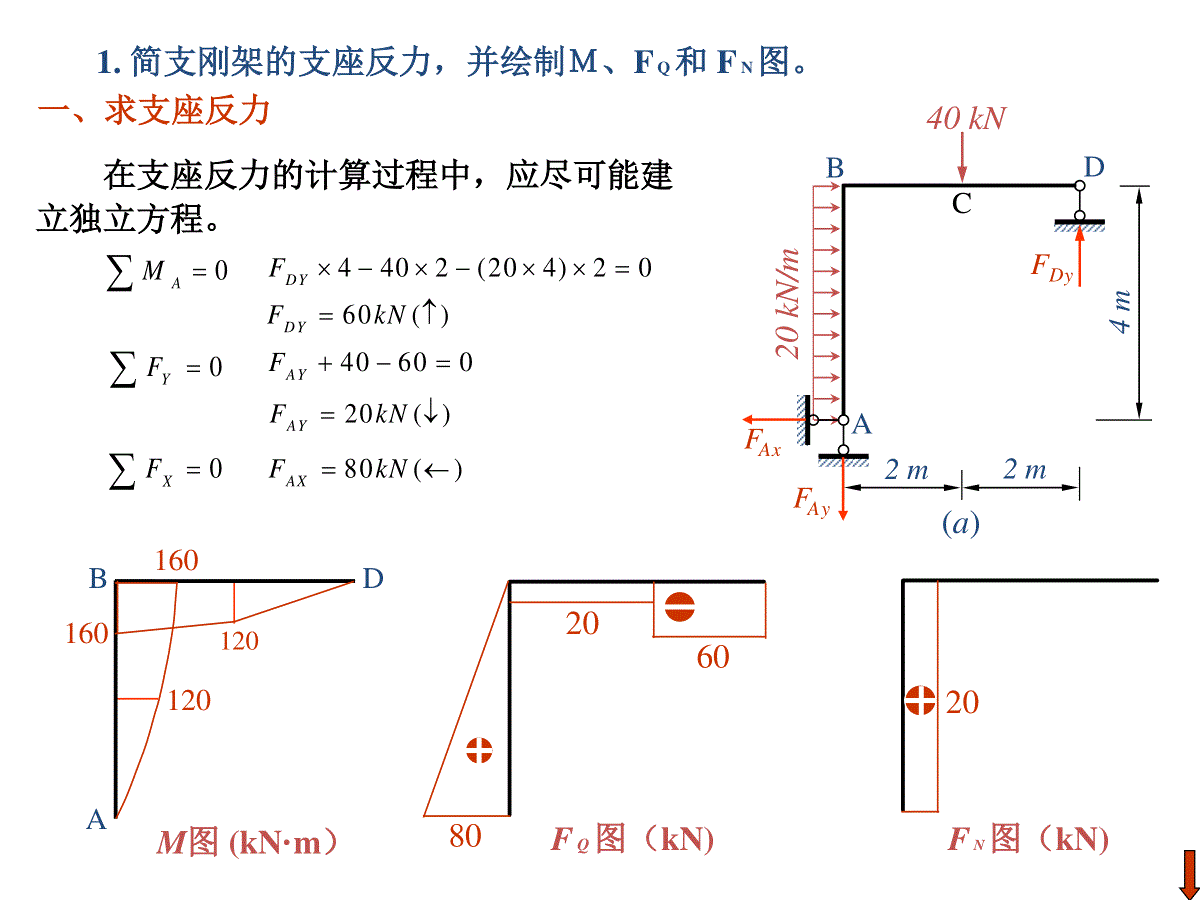
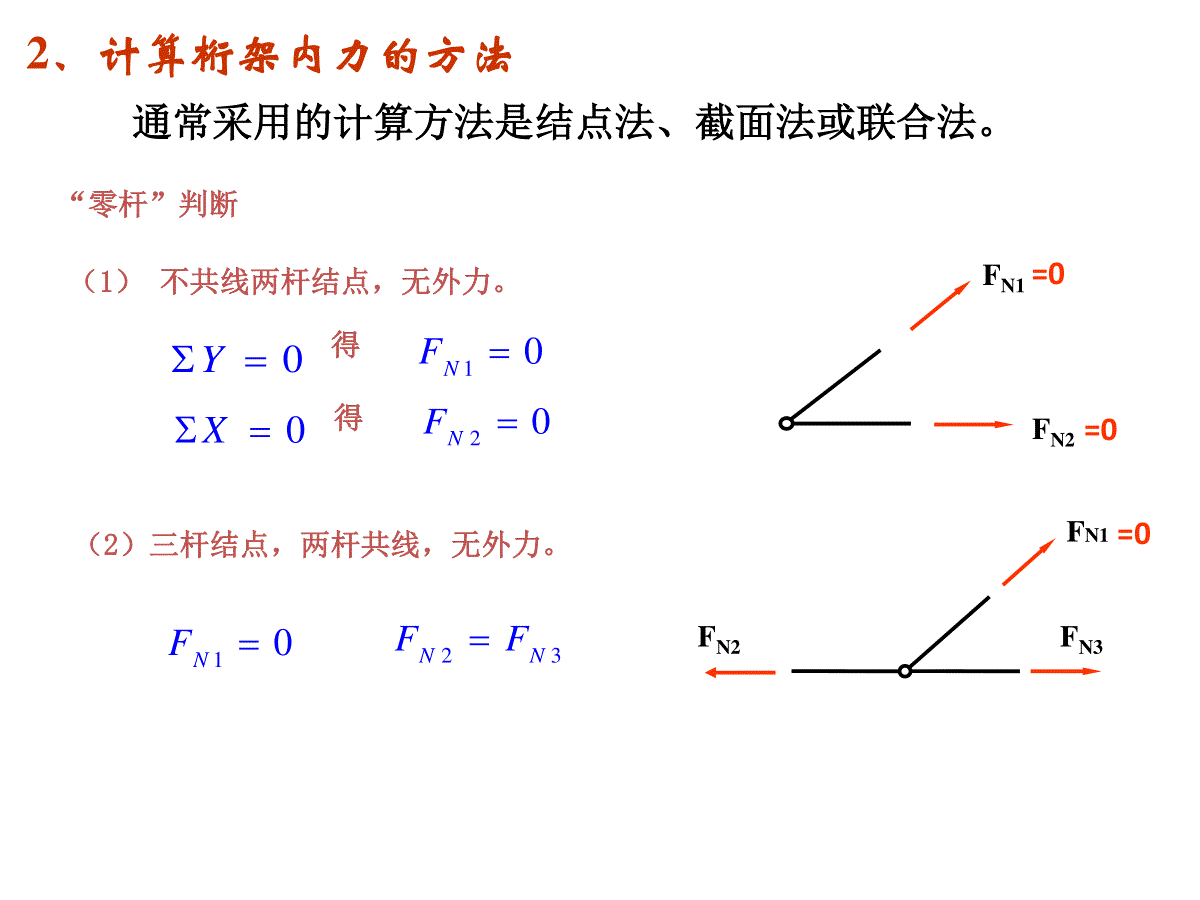
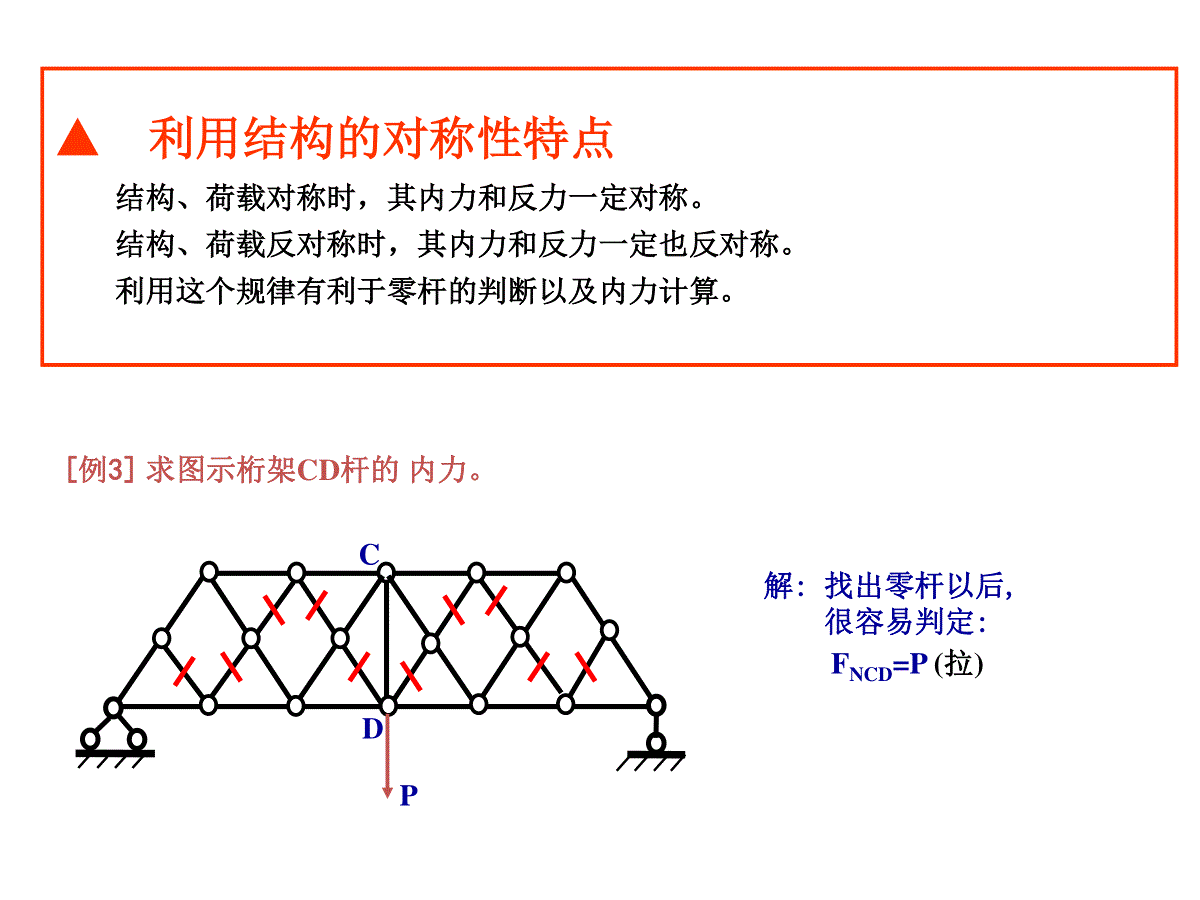
一、求支座反力在支座反力的计算过程中，应尽可能建立独立方程。1.简支刚架的支座反力，并绘制Ｍ、FQ和FN图。20kN/m40kN(a)ABDC4m2m2m0AM4402(204)20DYF60()DYFkN0YF40600AYF20()AYFkN0XF80()AXFkNFAyFAxFDy120FQ图（kN)120AM图(kN·m）BD160160206080FN图（kN)202、计算桁架内力的方法通常采用的计算方法是结点法、截面法或联合法。“零杆”判断FN1FN2（1）不共线两杆结点，无外力。0X0Y10NF20NF得得=0=0FN1FN3FN2（2）三杆结点，两杆共线，无外力。=010NF23NNFFPCD[例3]求图示桁架CD杆的内力。解:找出零杆以后,很容易判定:FNCD=P(拉)▲利用结构的对称性特点结构、荷载对称时，其内力和反力一定对称。结构、荷载反对称时，其内力和反力一定也反对称。利用这个规律有利于零杆的判断以及内力计算。[例4]：判断图示结构的零杆（对称和反对称两种情况）。00CDCEYFFFCDFCEFpFpACBDECFpFpACBDEDE杆的内力应该相对对称轴反对称分布，这就要求半根受拉、半根受压，这是不可能的，因此它是零杆。对称情况解：反对称情况解：机动法做静定梁内力（反力）影响线步骤：所作虚位移图要满足支承连接条件！如有竖向支撑处，不应有竖向位移。定向连接处左右杆段位移后要互相平行等。①去除与所求量值相应的约束，并代以正向的约束力。②使所得体系沿约束力的正方向发生相应的单位位移，由此得到的FP=1作用点的位移图即为该量值的影响线。③基线以上的竖标取正号，以下取负号。3.在影响线图形中，横坐标x表示单位移动荷载在梁上的位置；纵坐标y表示当单位荷载在该位置时，影响系数的大小。RAF2m2m2m1m2m2m1m4m2mABCDEFGHRCFABCDEFGH1RCF11.25.RCILFABCDEFGH110.51.MLI1练习：作I.L12,,,RCQQAFMFFFP=11M2m2m2m1m2m2m1m4m2mABCDEFGH2ABCDEFGHABCDEFGH1.02.QILF.QAILF2QFQAF1.00.250.254.力法步骤归纳:PMMXM111.确定超静定次数，选取基本体系；2.按照位移条件，写出力法典型方程；3.作单位弯矩图，荷载弯矩图；4.求出系数和自由项；5.解力法典型方程求多余未知力；6.用叠加法作弯矩图。111q计算超静定刚架和排架位移时，通常忽略轴力和剪力的影响，只考虑弯矩的影响，使计算简化。例：用力法求图示刚架M图。1、力法方程kIEIE22115.力法解超静定刚架MP图原结构ABCE1I1lE2I2lqq基本体系CABX2CABX1=1CACAB82qlM1图M2图X2=10022221211212111PPXXXX2、求系数和自由项kIEqlIEqlqllIEP22311321112424218132102PkkIElIEIEIEIElIElIEllIElIE13333)322(1)322(122221122112211221111X122223IEl1122()EIkEI1CABM2图X2=1222221126)312(1IEllIE将求得的系数代入力法方程就得到：解方程得：0246)1(3223222122kIEqlXIElXkkIEl036222122XIElXIEl04)1(2221kqlXXkk0221XX4312121kqlX4314122kqlX3、解方程求出多余力11CAM1图X1=13.讨论1）当k=02212816qlqlXX刚架弯矩图为：可见，柱AB相当于在横梁BC的B端提供了固定约束。BC281ql2161ql2）当k=13）当k=∞a)M图2565ql2141ql2281qlM图2161ql即E1I1很小或E2I2很大ABC刚架弯矩图如图a)示。即E1I1很大或E2I2很小。由于柱AB抗弯刚度趋近于零，只提供轴向支撑，故梁BC相当于简支梁，M图见图b)。结论：在荷载作用下，超静定结构的内力只与各杆抗弯刚度EI的比值k有关，而与杆件抗弯刚度EI的绝对值无关。若荷载不变，只要k不变，结构内力也不变。4312121kqlX4314122kqlX2161ql281qlb)M图281ql基本未知量的选取6.位移法求解超静定刚架内力结构独立线位移：为了减少未知量，引入与实际相符的两个假设：结点角位移数：结构上可动刚结点数即为位移法的结点角位移数。⑴忽略轴向力产生的轴向变形---变形后的曲杆与原直杆等长；⑵变形后的曲杆长度与其弦等长。上面两个假设导致杆件变形后两个端点距离保持不变。例：用位移法分析图示刚架：解：⑴基本未知量B、。⑵单元分析：由转角位移方程2634221.54412ABBBiMiii3(2)6BCBBMii2634441.54412BABBiMiii30.754DCiMiq=3kN/mBBq=3kN/m8m4mii2iABCDBBCMBCFQABFQBAMBAMABFQCDFQDCMDC642FABABABiMiiMlB0BM0(1)BABCMMa101.540(1)Bii⑶位移法方程：MBCMBAFQBAFQCDBC0xF0(2)QBAQCDFFa63.75240(2)Bii如何求杆端剪力?q=3kN/mFQABFQBAMBAMAB0ABBAQABQABMMFFl求剪力的通用公式：63341.50.75642BQBABiiFii21.54ABBMii41.54BABMii0.75DCMi0.750.18754QCDiFi1.50.93756(0)QBAQCDBFFiiqQABFQBAFMBAMABEIl'0QABQABQABFFFMBAMABq简支杆上荷载作用的剪力0QABF0QBAF'QABF'QBAF杆端弯矩作用的剪力0ABBAQABMMFl63.75240(2)Bii⑷解位移法方程：101.540(1)BiiiiB58.7737.0⑸求杆端弯矩，作弯矩图。=-13.896kN·mMBA=-4.422kN·mMBC=4.422kN·mMDC=-5.685kN·mABCD13.8964.4224.4225.685M图（kN·m）ABCD1.420.553FQ图（kN）21.54ABBMii0.7377.5821.54iiii0ABBAQABQABMMFFl⑹求杆端剪力，作剪力图。13.94.4234424.5861.42QBAFkN4.58610.58kN5.68501.424QCDFkN10.581.421.42位移法基本体系和典型方程例：用典型方程法计算图示结构，杆长均为L，EI为常数。解：1、未知量：BEV2、基本结构如上图所示3、位移法方程111122133121122223323113223333000PPpkZkZkZFkZkZkZFkZkZkZFMABCEDLLL原结构CMABEDZ3Z1Z24、求系数和自由项3ii4ik111108BMki取B结点：2ik212102EMki取E结点：FQEDFQBAFQBCk31313003QBAQBCQEDiFLFFikL取BE截面：Z1=1ABEDi4i2i3iM1图2ik121202BMki取B结点：4i4ik222208EMki取E结点：320066QBAQBCQEDFFiFLikL取BE截面：FQEDFQBAFQBCk32Z2=14i2i2i4iM2图3i/Lk131303BMikL取B结点：6i/Lk232306EMikL取E结点：233301215QBAQBCQEDiFLFiFLikL取BE截面：FQEDFQBAFQBCk33Z3=13i/L6i/L6i/LM3图MP图MF1P10BPMFM取B结点：F2P200EPMF取E结点：30000QBAQBCQEDPFFFF取BE截面：FQEDFQBAFQBCF3PM把系数和自由项代入位移法典型方程中，得：123123123238206280361560iiZiZZMLiiZiZZLiiiZZZLLL后面的计算省略了。力矩分配法理论基础：位移法；计算对象：杆端弯矩；计算方法：逐渐逼近的方法；适用范围：连续梁和无侧移刚架。表示杆端对转动的抵抗能力。在数值上=仅使杆端发生单位转动时需在杆端施加的力矩。1SAB=4i1SAB=3iSAB=i1SAB=0SAB：与杆的线刚度i（材料的E、横截面的I、杆长）及远端支承有关，而与近端支承无关。转动刚度S：7.力矩分配法分配系数SAB=4i1SAB=3i11SAB=i⑵分配系数CABDiABiACiAD如用位移法求解：AABAABABSiM4AACAACACSiMAADAADADSiM3MMABMACMAD0AMAADACABSSSM)(AADACABASMSSSMMSSMAADADMSSMAABABMSSMAACACMMAjAjAAjAjSS1设A点有力矩M，求MAB、MAC和MADMAAACB141432614BCBASS216131414CDCBSS例：用力矩分配法计算图示连续梁(列表)。ABCD6m6m4m4mEI=1EI=2EI=161ABi4182BCi61CDi6.04.032132BCBA333.0667.02111CDCB分配系数0.40.60.6670.333固端弯矩-6060-100100分配与传递-33.3-66.7-33.429.4442214.7-14.7-7.3-7.34.42.92.2-1.5-0.7-0.70.30.41.50.2-43.692.6-92.641.3-41.3杆端弯矩0100kN20kN/m56.443.66.9FQ图（kN）求支座反力：68.256.4B124.6ABCD6m6m4m4mEI=1EI=2EI=1100kN20kN/mABCDM图（kN·m）43.692.621.9133.141.351.868.2ABCD⑴整理原始数据，对单元和刚架进行局部编码和总体偏码。⑹解方程[K]{}={P}求出结点位移{}。8.矩阵位移法计算步骤⑵形成局部坐标糸的单元刚度矩阵。ek⑶形成整体坐标糸的单元刚度矩阵。ek⑷用单元集成法形成整体刚度矩阵。K⑸求局部坐标糸的单元等效结点荷载，转換成整体坐标糸的单元等效结点荷载，用单元集成法形成整体结构的等效结点荷载。eePPFeeTePTPP271）单元编号、结点编号、结点位移未知量编号及单元定位向量见图。2）求各单元刚度矩阵[k]e。各单元线刚度为：236EIiii147.21.2EIiii例:用矩阵位移法作连续梁的弯矩图，各杆EI相同。1(0)2(1)3(2)4(3)5(0)1T{}[0,1]2T{}[1,2]3T{}[2,3]4T{}[3,0]③④①②①②1kN/m7.2m6m6m7.2m1kN/m解:283）集成整体刚度矩阵[K]。利用单元定位向