当前位置:首页 > 中学教育 > 初中教育 > 分式方程应用题中考题集
1/29分式性质及运算【基础精讲】一、分式的概念1、正确理解分式的概念:【例1】有理式(1)x1;(2)2x;(3)yxxy2;(4)33yx;(5)11-x;(6)1中,属于整式的有:;属于分式的有:。.2、判断分式有无意义关键是看分母是否为零.(1)例如,当x为时,分式322xxx有意义.错解:3x时原分式有意义.(2)不要随意用“或”与“且”。例如当x____时,分式有意义?错解:由分母,得3、注意分式的值为零必受分母不为零的限制.当x时,分式11-xx有意义.当x时,分式11-xx无意义.当x时,分式112-xx值为0.二、分式的基本性质:1、分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.(1)分式的基本性质是分式恒等变形的依据,它是分式的约分、通分、化简和解分式方程基础,因此,我们要正确理解分式的基本性质,并能熟练的运用它.理解分式的基本性质时,必须注意:①分式的基本性质中的A、B、M表示的都是整式.②在分式的基本性质中,M≠0.③分子、分母必须“同时”乘以M(M≠0),不要只乘分子(或分母).④性质中“分式的值不变”这句话的实质,是当字母取同一值(零除外)时,变形前后分式的值是相等的。但是变形前后分式中字母的取值范围是变化的.(2)注意:①根据分式的基本性质有:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变.②分式的基本性质是一切分式运算的基础,分子与分母只能同乘以(或除以)同一个不等于零的整式,而不能同时加上(或减去)同一个整式【例3】下列变形正确的是().A.ababcc;B.aabcbcC.ababababD.abababab2/29【例4】如果把分式52xxy中的,xy都扩大3倍,那么分式的值一定().A.扩大3倍B.扩大9倍C.扩大6倍D.不变2、约分约分是约去分式的分子与分母的最大公约式,约分过程实际是作除法,目的在于把分式化为最简分式或整式,根据是分式的基本性质.【例5】(1)化简222abaab的结果为()A.baB.abaC.abaD.b(2)化简2244xyyxx的结果()A.2xxB.2xxC.2yxD.2yx(3)化简62962xxx的结果是()A.23xB.292xC.292xD.23x3、通分通分的依据是分式的基本性质,通分的关键是确定最简公分母.最简公分母由下面的方法确定:(1)最简公分母的系数,取各分母系数的最小公倍数;(2)最简公分母的字母,取各分母所有字母的最高次幂的积;三、分式的运算1、分式运算时注意:(1)注意运算顺序.例如,计算aaaa31)3(11,应按照同一级运算从左到存依次计算的法则进行.错解:原式2)1(1)1(11aaa(2)通分时不能丢掉分母.例如,计算11xxx,出现了这样的解题错误:原式=11xx.分式通分是等值变形,不能去分母,不要同解方程的去分母相混淆;(3)忽视“分数线具有括号的作用”:分式相减时,若分子是多项式,其括号不能省略.(4)最后的运算结果应化为最简分式.2、分式的乘除注意分式的乘除法应用关键是理解其法则.(1)先把除法变为乘法;(2)接着对每个相乘的分式的分子、分母进行因式分解,当然有乘方运算要先算乘方,然后同其它分式进行约分;(3)再把每个分式的分子与分子相乘、分母与分母相乘;(4)最后还应检查相乘后的分式是否为最简分式.3、加减的加减1)同分母分式加减法则:分母不变,分子相加减。2)异分母分式加减法则:运算步骤:①先确定最简公分母;②对每项通分,化为分母相同;③按同分母分式运算法则进行;④注意结果可否化简,化为最简.4、分式的混合运算3/29注意分式的混合运算的顺序:先进行乘方运算,其次进行乘、除运算,再进行加、减运算,遇有括号,先算括号内的.如果分式的分子或分母中含有多项式,并且能分解因式,可先分解因式,能约分的先约分,再进行运算.【例6】计算:(1)212242aaaa;(2)222xxx;(3)xxxxxx2421212(4)已知113xy,则代数式21422xxyyxxyy的值【分类解析】一、分式运算的几种技巧1、先约分后通分技巧例1计算2312xxx+4222xxx2、分离整数技巧例2计算233322xxxx-657522xxxx-3412xx3、裂项相消技巧例3计算)1(1xx+)3)(1(2xx+)6)(3(3xx4、分组计算技巧例4计算21a+12a-12a-21a5、变形技巧例5已知x2-3x+1=0,求x2+21x的值。二、分式求值中的整体思想例1若分式73222yy的值为41,则21461yy的值为()A、1B、-1C、-71D、51例2已知a1+b1=4,则babababa323434=。例3已知a2-3a+1=0,求142aa的值。4/29例4已知a1+b1=61,b1+c1=91,a1+c1=151,求bcacababc的值。例5有一道题:“先化简再求值:22x12x1)x1x1x1(,其中x=2008”,小明做题时把“x=2008”错抄成了“x=2008”,但他的计算结果也是正确,请你通过计算解释这是怎么回事?例6已知x2-3x+1=0,求x2+21x的值。三、分式运算新型题例2请利用31m、3mm和932m这三个分式组成一个算式,来表示其中两个分式的商减去第三个分式的差,并化简.例3先化简代数式222aaa÷412a,然后选取一个合适..的a值,代入求值.一、开放性问题例1在下列三个不为零的式子44,2,4222xxxxx中,任选两个你喜欢的式子组成一个分式是,把这个分式化简所得的结果是.分析:此例是答案不唯一的开放题,分式由学生自主构造,题型新颖活泼,呈现出人性化与趣味化.解:本题存在6种不同的结果,任选其一即可.(1)xx,xxx22422;(2)2244422xx,xxx;(3)244222xx,xxxx;(4)24222xx,xxx;(5)2244422xx,xxx;(6)xx,xxxx224422.5/29二、探索运算程序例2任意给定一个非零数,按下列程序计算,最后输出的结果是()m平方-m÷m+2结果A.mB.m2C.m+1D.m-1三、自选数值求解例3化简2111xxxx,并选择你最喜欢的数代入求值.四、运算说理题例4在解题目:“当1949x时,求代数式2224421142xxxxxxx的值”时,聪聪认为x只要任取一个使原式有意义的值代入都有相同结果.你认为他说的有理吗?请说明理由.分析:本题是说理型试题,有很强的创新性,但将其转化为代数式的化简与求值,解决问题就很方便,同时要注意说的“理由”要充分合理.解:聪聪说的有理.2224421142xxxxxxx2(2)211(2)(2)(2)xxxxxxx111xx1∴只要使原式有意义,无论x取何值,原式的值都相同,为常数1.说明:解决此类问题,首先要化简所给的代数式,然后再根据化简的结果去解释题目所问的问题.先观察下列等式,然后用你发现的规律解答下列问题.11112211123231113434┅┅(1)计算111111223344556.(2)探究1111......122334(1)nn.(用含有n的式子表示)(3)若1111......133557(21)(21)nn的值为1735,求n的值.6/29【精练】计算:1.顺次相加法例1:计算:2.整体通分法【例2】计算:3.化简后通分4.巧用拆项法例4计算:.5.分组运算法例5:计算:二、经典例题透析类型一:分式及其基本性质1.当x为任意实数时,下列分式一定有意义的是()A.B.C.D.2.若分式的值等于零,则x=_______;7/293.求分式的最简公分母。【变式1】(1)已知分式的值是零,那么x的值是()A.-1B.0C.1D.±1(2)当x________时,分式没有意义.【变式2】下列各式从左到右的变形正确的是()A.B.C.D.类型二:分式的运算技巧(一)通分约分4.化简分式:【变式1】顺次相加法计算:【变式2】整体通分法计算:(二)裂项或拆项或分组运算5.巧用裂项法计算:【变式1】分组通分法计算:【变式2】巧用拆项法计算:类型三:条件分式求值的常用技巧6.参数法已知,求的值.【变式1】整体代入法已知,求的值.8/29【变式2】倒数法:在求代数式的值时,有时出现条件或所求分式不易变形,但当分式的分子、分母颠倒后,变形就非常的容易,这样的问题适合通常采用倒数法.已知:,求的值.【变式3】主元法:当已知条件为两个三元一次方程,而所求的分式的分子与分母是齐次式时,通常我们把三元看作两元,即把其中一元看作已知数来表示其它两元,代入分式求出分式的值.已知:,求的值.类型四:解分式方程的方法解分式方程的基本思想是去分母,课本介绍了在方程两边同乘以最简公分母的去分母的方法,现再介绍几种灵活去分母的技巧.(一)与异分母相关的分式方程7.解方程=【变式1】换元法解方程:32121xxx(二)与同分母相关的分式方程8.解方程3323xxx【变式1】解方程87178xxx【变式2】解方程125552xxx类型五:分式(方程)的应用9.甲、乙两个小商贩每次都去同一批发商场买进白糖.甲进货的策略是:每次买1000元钱的糖;乙进货的策略是每次买1000斤糖,最近他俩同去买进了两次价格不同的糖,问两人中谁的平均价格低一些?【变式1】甲开汽车,乙骑自行车,从相距180千米的A地同时出发到B.若汽车的速度是自行车的速度的2倍,汽车比自行车早到2小时,那么汽车及自行车的速度各是多少?【变式2】A、B两地路程为150千米,甲、乙两车分别从A、B两地同时出发,相向而行,2小时后相遇,相遇后,各以原来的速度继续行驶,甲车到达B后,立即沿原路返回,返回时的速度是原来速度的2倍,结果甲、乙两车同时到达A地,求甲车原来的速度和乙车的速度.【主要公式】1.同分母加减法则:0bcbcaaaa2.异分母加减法则:0,0bdbcdabcdaacacacacac;3.分式的乘法与除法:bdbdacac,bcbdbdadacac4.同底数幂的加减运算法则:实际是合并同类项5.同底数幂的乘法与除法;am●an=am+n;am÷an=am-n6.积的乘方与幂的乘方:(ab)m=ambn,(am)n=amn9/297.负指数幂:a-p=1paa0=18.乘法公式与因式分解:平方差与完全平方式(a+b)(a-b)=a2-b2;(a±b)2=a2±2ab+b2(一)、分式定义及有关题型题型一:考查分式的定义【例1】下列代数式中:yxyxyxyxbabayxx1,,,21,22,是分式的有:.题型二:考查分式有意义的条件【例2】当x有何值时,下列分式有意义(1)44xx(2)232xx(3)122x(4)3||6xx(5)xx11题型三:考查分式的值为0的条件【例3】当x取何值时,下列分式的值为0.(1)31xx(2)42||2xx(3)653222xxxx题型四:考查分式的值为正、负的条件【例4】(1)当x为何值时,分式x84为正;(2)当x为何值时,分式2)1(35xx为负;(3)当x为何值时,分式32xx为非负数.练习:1.当x取何值时,下列分式有意义:(1)3||61x(2)1)1(32xx(3)x1112.


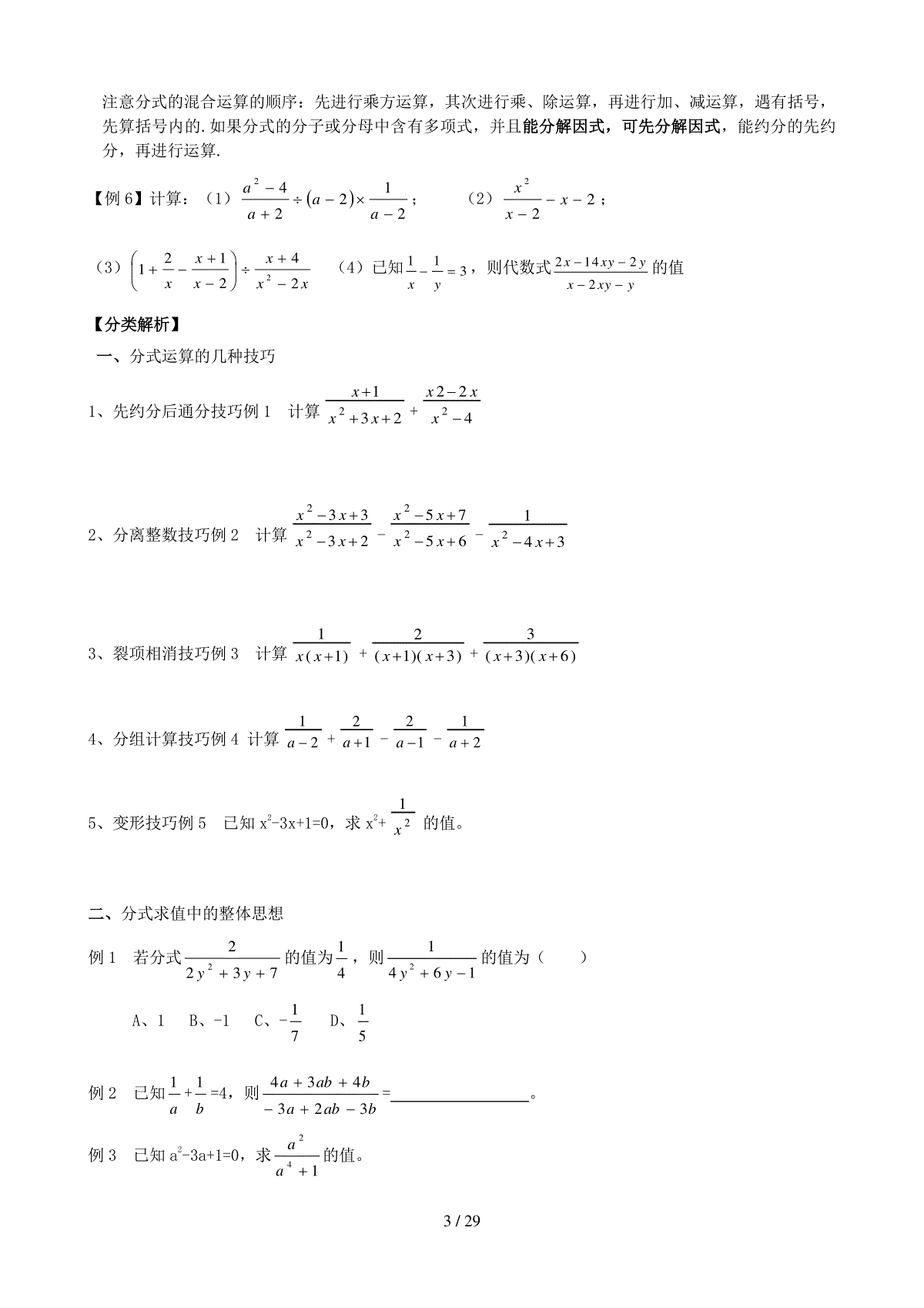


 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:分式方程应用题中考题集
链接地址:https://www.777doc.com/doc-3181466 .html