当前位置:首页 > 中学教育 > 高中教育 > 高一数学求函数解析式方法总结
求函数的解析式一.配凑法把形如f(g(x))内的g(x)当做整体,在解析式的右端整理成只含有g(x)的形式,再把g(x)用x代替。一般的利用完全平方公式。已知f(g(x))的解析式,求f(h(x))的解析式,已知22)1(2xxxf,求(3),3ffxfx及解:22)1(2xxxf1)1(2x1122xx1)(2xxf223(3)1610yfxxxx310f练习:1.已知f(x+1)=x-3,求f(x)2.若xxxf2)1(,求)(xf的解析式1)f(x+1)=x-3=x+1-4∴f(x)=x-42)1)1(1122)1(2xxxxxxf∴f(x)=x2-1,(x≥1)例1已知f()=+,求f(x).xx+1x2x2+1x1∴f(x)=x2-x+1(x≠1).解:∵f()=+xx+1x2x2+1x1=1++x21x1=(+1)2-(+1)+1x1x1并且≠1,xx+1=()2-()+1xx+1xx+1评注:若在给出的函数关系式中与的关系不明显时,要通过恒等变形寻找二者的关系.+x2x2+1x1xx+1二.换元法已知f(g(x)),求f(x)的解析式,一般的可用换元法,具体为:令t=g(x),在求出f(t)可得f(x)的解析式。换元后要确定新元t的取值范围。)(,23)1(2xfxxxf求已知令t=x+1,则x=t-1∴f(t)=f(x+1)=(t-1)2-3(t-1)+2=t2-2t+1-3t+3+2=t2-5t+6∴f(x)=x2-5x+6例2.已知22)1(2xxxf,求(3),3ffxfx及解:22)1(2xxxf1)1(2x1122xx1)(2xxf分析:这是含有未知函数f(x)的等式,比较抽象。由函数f(x)的定义可知,在函数的定义域和对应法则f不变的条件下,自变量变换字母,以至变换为其他字母的代数式,对函数本身并无影响,这类问题正是利用这一性质求解的。方法一:223(3)1610yfxxxx310f配凑法二、换元法方法二:令1,1txxt则22212212121ftfxxxttt,21fxx.223(3)1610yfxxxx换元法注意点:注意换元的等价性,即要求出t的取值范围.310f.练习.已知f()=x2+5x,则f(x)=.解析)0(512xxx).()(),()()(),(,,0510511510110222xxxxfttttttfttxtxx故即令·x1三.待定系数法已知函数模型(如:一次函数,二次函数,等)求解析式,首先设出函数解析式,根据已知条件代入求系数例2已知f(x)是二次函数,且442)1()1(2xxxfxf求).(xf解:cbxaxxf2)(设cabxaxxfxf2222)1()1(24422xx1,2,1cba12)(2xxxf)0(a练习:1.的解析式求一次函数若)(,14))((xfxxff设:f(x)=ax+b,则f(f(x))=a(ax+b)+b=a2x+ab+b=4x-1∴a2=4,ab+b=-1∴a=2,b=或a=-2,b=1f(x)=2x-或f(x)=-2x+131312.已知函数是一次函数,且经过(1,2),(2,5)求函数的解析式)(xf)(xfy设f(x)=ax+b,由题知:f(1)=2,f(2)=5即a+b=2,2a+b=5∴a=3,b=-1∴f(x)=3x+b四.方程组法求抽象函数的解析式,往往通过变换变量构造一个方程,组成方程组,利用消元法求f(x)的解析式例3.设f(x)满足关系式求函数的解析式123fxfxxxxfxfxxfxf3)(2)1(3)1(2)(解:令xx1联立方程,得:xxfxf13)(2)1(解得xxxf2)(练习:若3f(x)+f(-x)=2–x,求f(x).解:令x=-x,则3f(-x)+f(x)=2+x联立方程组,得:xxfxfxxfxf2)()(32)()(3解得:xxf2121解方程组法例3已知f(x)+f()=1+x(x≠0,1),求f(x).xx-1解:记题中式子为①式,用代替①中的x,整理得:xx-1f()+f()=②,xx-11-x1x2x-1再用代替①中的x,整理得:1-x1f()+f(x)=③,1-x11-x2-x解由①,②,③组成的方程组,得:2x(x-1)x3-x2-1f(x)=.例4.设f(x)满足关系式求函数的解析式.•分析:如果将题目所给的看成两个变量,那么该等式即可看作二元方程,那么必定还需再找一个关于它们的方程,那么交换x与1/x形成新的方程123fxfxx1,fxfx123(1)123132(2)21201111FxfxfxxFffffxxxxxxfxxxxx解:设有()()得【练习】(1)设二次函数f(x)满足f(x-2)=f(-x-2),且图象在y轴上的截距为1,被x轴截得的线段长为,求f(x)的解析式;(2)已知(3)已知f(x)满足2f(x)+=3x,求f(x).问题(1)由题设f(x)为二次函数,故可先设出f(x)的表达式,用待定系数法求解;问题(2)已知条件是一复合函数的解析式,因此可用换元法;问题(3)已知条件中含x,,可用解方程组法求解.22);(,2)1(xfxxxf求)1(xfx1思维启迪解:(1)∵f(x)为二次函数,∴设f(x)=ax2+bx+c(a≠0),且f(x)=0的两根为x1,x2.由f(x-2)=f(-x-2),得4a-b=0.①②由已知得c=1.③由①、②、③式解得b=2,a=,c=1,∴f(x)=x2+2x+1..84,22||4||22221aacbaacbxx又2121).()(,,)()()().()(),()(,)(.1),()(1111111122111112111222222xxxfxxxxxxxfxxxftttfxxxftxttx且得代入则设方法二方法一).0(12)(,36)(3②2①②3)()1(2①3)1()(2,3)()1(2,1)3(xxxxfxxxfxxfxfxxfxfxxfxfxx所以得联立方程得换成把题目中的五.赋值法五.赋值法一般的,已知一个关于x,y的抽象函数,利用特殊值去掉一个未知数y,得出关于x的解析式。解:yyxyxfyxf22)()(已知定义在R上的函数f(x),对任意实数x,y满足:求).(xf,且1)0(f得令yxxxxxff222)()0(1)(2xxxf练习:已知函数对于一切实数都有)(xfyx,xyxyfyxf)12()()(成立,且0)1(f1.求)0(f的值.)(.2的解析式求xf令x=1,y=0得f(1+0)-f(0)=(1+2×0+1)×1即0-f(0)=2解得f(0)=-2令y=0得f(x+0)-f(0)=(x+2×0+1)x即f(x)-(-2)=x(x+1)解得f(x)=x2+x-2六.根据图象写出解析式六.根据图象写出解析式观察图像的特点和特殊点,可用代入法,或根据函数图像的性质进行解题。注意定义域的变化。如下图,函数图象是两个部分抛物线构成,求函数的解析式解:当x≥1时,函数图象是对称轴为x=2,顶点坐标为(2,1)的图象解析式为y=(x-2)2+1,x≥1当x<1时,函数图象为是对称轴x=0,顶点坐标为(0,1)的图象解析式为y=x2+1,x<1函数的解析式为{y=(x-2)2+1,x≥1y=x2+1,x<1f(x)的图象如图,则f(x)=当x∈[-2,0)时,323xyxy32当x∈[0,3]时,∴f(x)=[0,3],32-)0,2[-,332xxxx


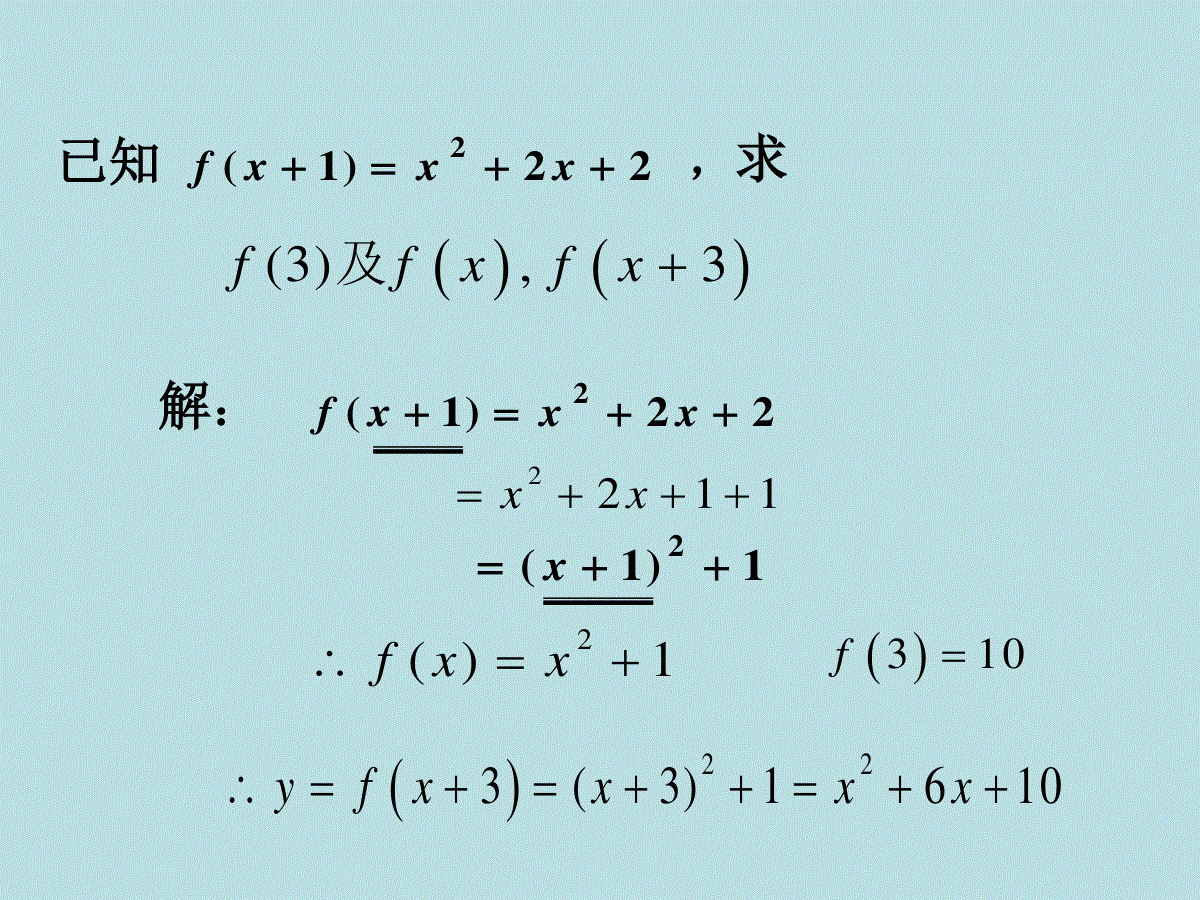
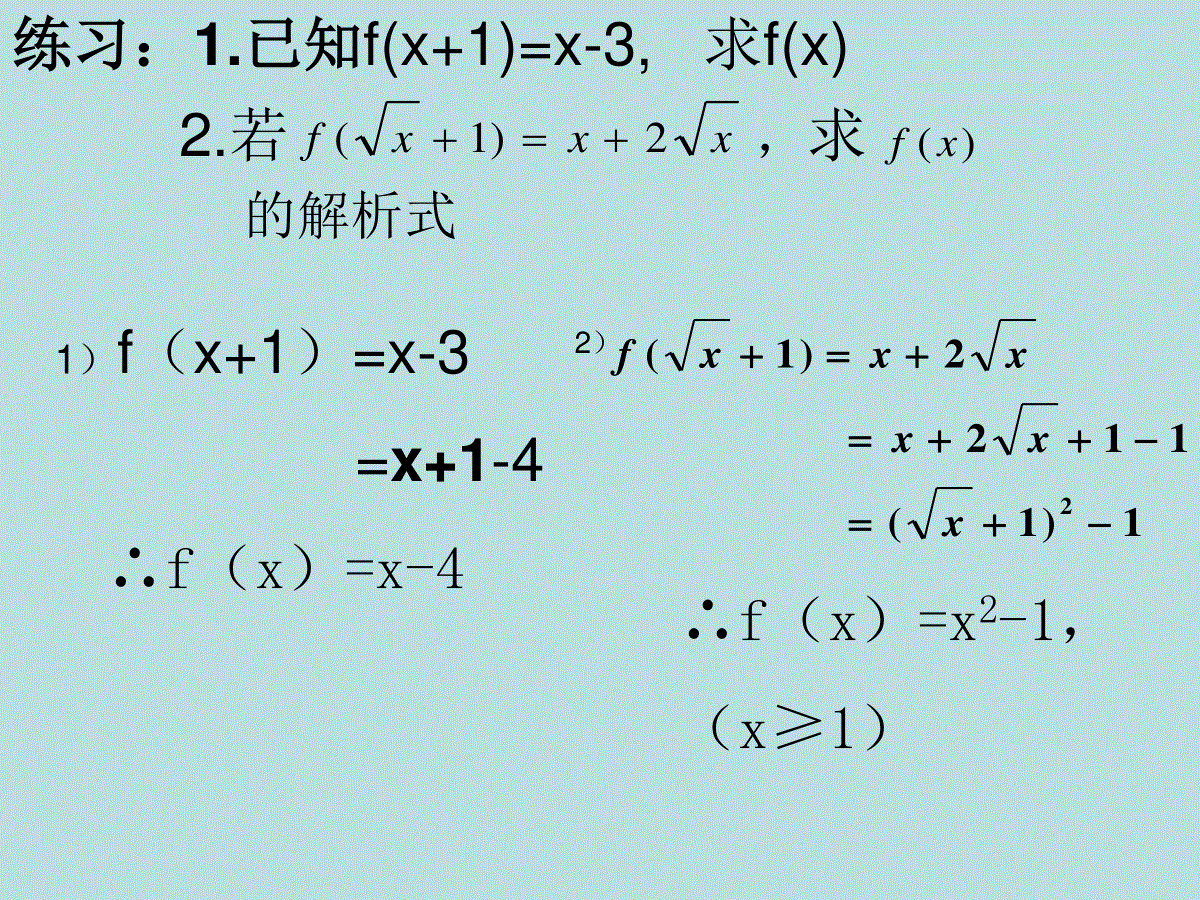

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:高一数学求函数解析式方法总结
链接地址:https://www.777doc.com/doc-3713967 .html