天津市2019年中考数学试题研究与圆有关的证明与计算

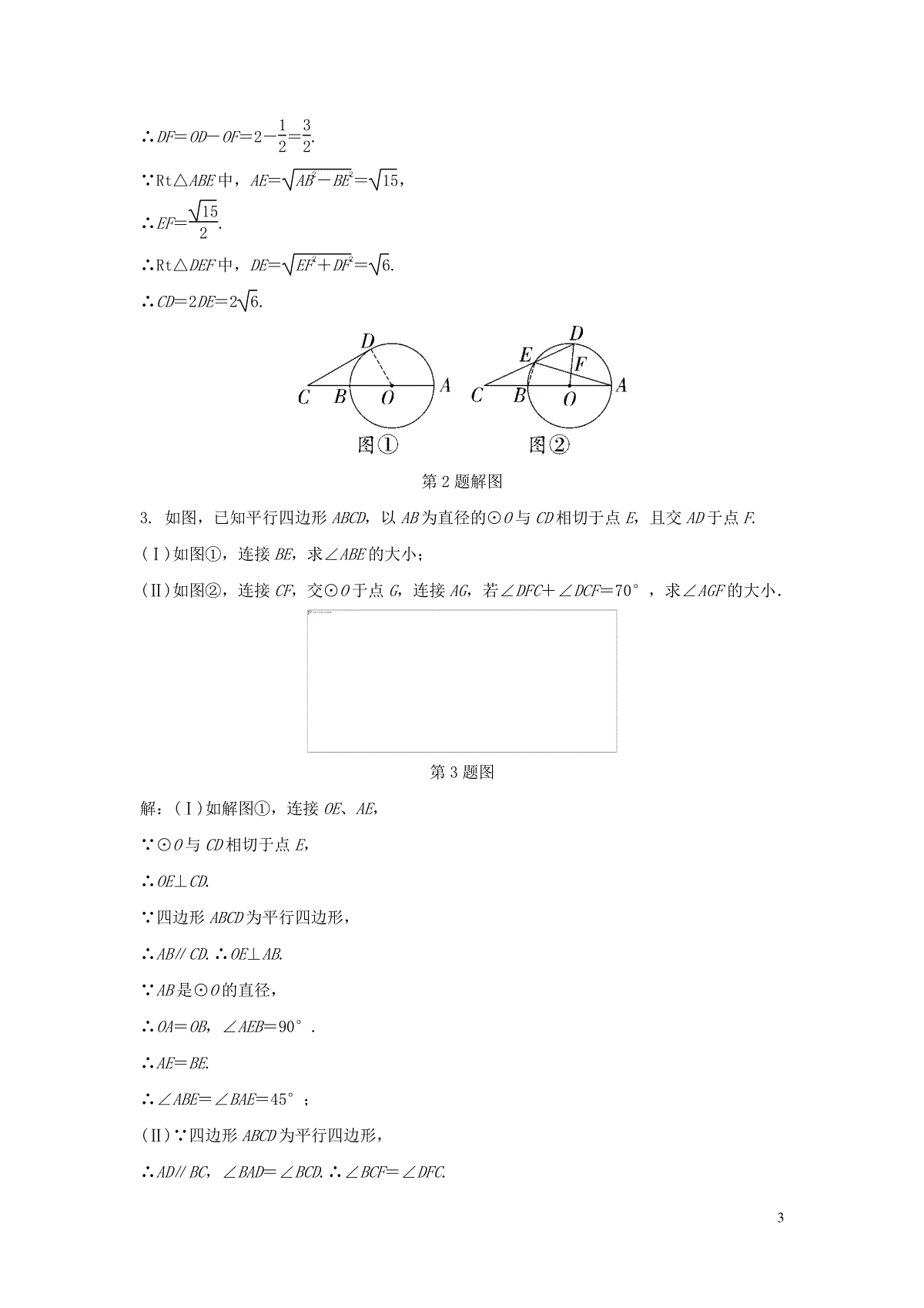
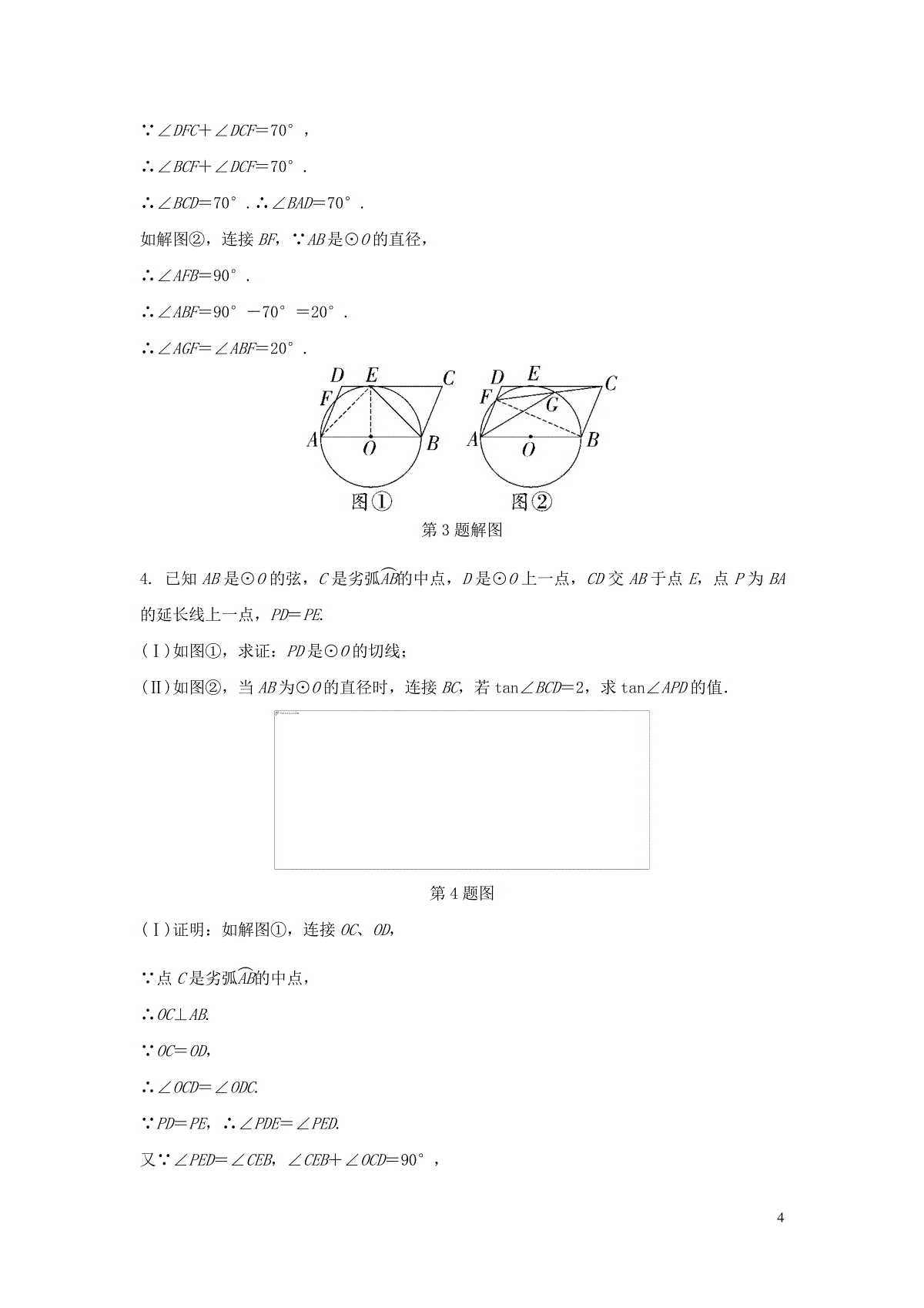
1与圆有关的证明与计算1.在△ABC中，∠ABC＝45°，∠C＝60°，⊙O经过点A、B，与BC交于点D，连接AD.(Ⅰ)如图①，若AB是⊙O的直径，交AC于点E，连接DE，求∠ADE的大小．(Ⅱ)如图②，若⊙O与AC相切，求∠ADC的大小．第1题图解：(Ⅰ)如解图①，连接BE，∵∠ABC＝45°，∠C＝60°，∴∠BAC＝75°.∵AB是⊙O的直径，∴∠AEB＝90°.∴∠ABE＝∠AEB－∠BAC＝15°.∵∠ABE＝∠ADE，∴∠ADE＝15°；(Ⅱ)如解图②，连接OA，OD，∵AC是⊙O的切线，∴∠OAC＝90°.∵∠ABC＝45°，∴∠AOD＝90°.∵OA＝OD，∴∠OAD＝45°.∴∠DAC＝∠OAC－∠OAD＝45°.∵∠C＝60°，∴∠ADC＝75°.2第1题解图2.如图，AB是⊙O的直径，且AB＝4，点C在AB延长线上，且BC＝2，点D是⊙O上一点，连接CD.(Ⅰ)如图①，若CD与⊙O相切，求CD的长；(Ⅱ)如图②，若CD与⊙O的另一个交点为点E，且E为CD的中点，连接OD、AE交于点F，求CD的长．第2题图解：(Ⅰ)如解图①，连接OD，∵CD与⊙O相切，∴OD⊥CD，即∠ODC＝90°.又∵AB是⊙O的直径，且AB＝4，BC＝2，∴OD＝OB＝OA＝2，OC＝4.∴Rt△COD中，CD＝42－22＝23；(Ⅱ)如解图②，连接BE，∵AB是⊙O的直径，∴∠AEB＝90°.∵点E为CD的中点，BC＝OB＝OD＝2，∴BE∥OD，BE＝12OD＝1.∴∠AFO＝∠AEB＝90°.∴OD⊥AE，AF＝EF.又∵O是AB的中点，∴OF＝12BE＝12.3∴DF＝OD－OF＝2－12＝32.∵Rt△ABE中，AE＝AB2－BE2＝15，∴EF＝152.∴Rt△DEF中，DE＝EF2＋DF2＝6.∴CD＝2DE＝26.第2题解图3.如图，已知平行四边形ABCD，以AB为直径的⊙O与CD相切于点E，且交AD于点F.(Ⅰ)如图①，连接BE，求∠ABE的大小；(Ⅱ)如图②，连接CF，交⊙O于点G，连接AG，若∠DFC＋∠DCF＝70°，求∠AGF的大小．第3题图解：(Ⅰ)如解图①，连接OE、AE，∵⊙O与CD相切于点E，∴OE⊥CD.∵四边形ABCD为平行四边形，∴AB∥CD.∴OE⊥AB.∵AB是⊙O的直径，∴OA＝OB，∠AEB＝90°.∴AE＝BE.∴∠ABE＝∠BAE＝45°；(Ⅱ)∵四边形ABCD为平行四边形，∴AD∥BC，∠BAD＝∠BCD.∴∠BCF＝∠DFC.4∵∠DFC＋∠DCF＝70°，∴∠BCF＋∠DCF＝70°.∴∠BCD＝70°.∴∠BAD＝70°.如解图②，连接BF，∵AB是⊙O的直径，∴∠AFB＝90°.∴∠ABF＝90°－70°＝20°.∴∠AGF＝∠ABF＝20°.第3题解图4.已知AB是⊙O的弦，C是劣弧AB︵的中点，D是⊙O上一点，CD交AB于点E，点P为BA的延长线上一点，PD＝PE.(Ⅰ)如图①，求证：PD是⊙O的切线；(Ⅱ)如图②，当AB为⊙O的直径时，连接BC，若tan∠BCD＝2，求tan∠APD的值．第4题图(Ⅰ)证明：如解图①，连接OC、OD，∵点C是劣弧AB︵的中点，∴OC⊥AB.∵OC＝OD，∴∠OCD＝∠ODC.∵PD＝PE，∴∠PDE＝∠PED.又∵∠PED＝∠CEB，∠CEB＋∠OCD＝90°，5∴∠PDE＋∠ODC＝90°，即∠PDO＝90°.∵OD是⊙O的半径，∴PD是⊙O的切线；(Ⅱ)解：如解图②，连接AD、OD、BD，∵AB是⊙O的直径，∴∠ADB＝90°.∵∠BAD＝∠BCD，∴tan∠BAD＝BDAD＝tan∠BCD＝2.∵PD是⊙O的切线，∴∠ODP＝90°.∴∠PBD＝∠ADP，又∵∠P＝∠P，∴△APD∽△DPB.∴PAPD＝PDPB＝ADDB＝12.设PA＝a，则PD＝2a，PB＝4a，则AB＝3a，∴OD＝32a.∴tan∠APD＝ODPD＝34.图①图②第4题解图5.已知BC是⊙O的直径，AD是⊙O的切线，切点为A，AD交CB的延长线于点D，连接AB，AO.(Ⅰ)如图①，求证：∠OAC＝∠DAB；(Ⅱ)如图②，若AD＝AC，E是⊙O上一点，连接AE、BE，求∠E的大小．6第5题图(Ⅰ)证明：∵AD是⊙O的切线，切点为A，∴DA⊥AO.∴∠DAO＝90°.∴∠DAB＋∠BAO＝90°.∵BC是⊙O的直径，∴∠BAC＝90°.∴∠BAO＋∠OAC＝90°.∴∠OAC＝∠DAB；(Ⅱ)解：∵OA＝OC，∴∠OAC＝∠C.∵AD＝AC，∴∠D＝∠C.∴∠OAC＝∠D.∵∠OAC＝∠DAB，∴∠DAB＝∠D.∵∠ABC＝∠D＋∠DAB，∴∠ABC＝2∠D.∵∠D＝∠C，∴∠ABC＝2∠C.∵∠BAC＝90°，∴∠ABC＋∠C＝90°.∴2∠C＋∠C＝90°.∴∠C＝30°.∴∠E＝∠C＝30°.6.已知▱ABCD的边AD与经过A、B、C三点的⊙O相切于点A.(Ⅰ)如图①，连接AC，若∠D＝32°，求∠ACD的大小；(Ⅱ)如图②，延长DC交⊙O于点E，连接BE，若sin∠E＝1213，⊙O的半径为13，求BC的长．7第6题图(Ⅰ)如解图①，连接OA，∵AD与⊙O相切于点A，∴OA⊥AD.∵四边形ABCD是平行四边形，∴AB∥CD，BC∥AD，∠B＝∠D＝32°.∴OA⊥BC，∠ACD＝∠BAC.∴AB＝AC.∴∠B＝∠ACB.∴∠BAC＝180°－2∠B＝116°.∴∠ACD＝116°；(Ⅱ)如解图②，作直径BF，连接CF.∵BF为⊙O的直径，∴∠BCF＝90°.∵∠F＝∠E，BF＝26，∴在Rt△BCF中，sin∠F＝BCBF＝sin∠E＝1213.∴BC＝1213×26＝24.第6题解图7.已知AB是⊙O的直径，AB＝10，弦BC＝6，点D在⊙O上，与点C分别在AB两侧，过点D作⊙O的切线PD.(Ⅰ)如图①，DP与AB延长线交于点P，连接PC，若PC与⊙O相切，求AD的长．(Ⅱ)如图②，若切线PD∥AB，求AD的长8图①图②第7题图解：(Ⅰ)如解图①，连接OD，∵PC和PD为⊙O的切线，∴PC＝PD，OP平分∠CPD.∴PA⊥CD.∴BC︵＝BD︵.∴BD＝BC＝6.∵AB为⊙O的直径，∴∠ADB＝90°.∴AD＝AB2－BD2＝8；第7题解图①(Ⅱ)如解图②，连接OD，BD，∵PD为⊙O的切线，∴PD⊥OD.∵AB∥PD，∴OD⊥AB.∴AD︵＝BD︵.∴AD＝BD.∵AB为⊙O的直径，∴∠ADB＝90°，∠ACB＝90°.∴△ABD为等腰直角三角形.∴AD＝22AB＝52.9第7题解图②8.在△ABC中，AB＝AC，以AB为直径的⊙O分别交边BC、AC于点D、点E，且AE＝BE.(Ⅰ)如图①，求∠EBC的度数；(Ⅱ)如图②，过点D作⊙O的切线交AB的延长线于点G，交AC于点F，若⊙O的直径为10，求BG的长．第8题图解：(Ⅰ)∵AB为⊙O的直径，∴∠AEB＝90°.∵AE＝BE，∴∠A＝∠ABE＝45°.∵AB＝AC，∴∠ABC＝∠ACB＝12×(180°－45°)＝67.5°，∴∠EBC＝∠ABC－∠ABE＝22.5°；(Ⅱ)如解图，连接OD、AD，∵FG是⊙O的切线，∴GF⊥OD.∴∠ODG＝90°.∵AB为⊙O的直径，∴∠ADB＝90°.∴AD⊥BC.∵AB＝AC，∴BD＝DC.∵OA＝OB，∴OD∥AC.∴∠GOD＝∠BAC＝45°.10∴cos∠GOD＝ODOG＝22，∵⊙O的直径为10，∴OB＝OD＝5.∴OG＝52.∴BG＝52－5.第8题解图9.正方形ABCD内接于⊙O，过点A作⊙O的切线交CD延长线于点P.(Ⅰ)如图①，求∠P的大小；(Ⅱ)如图②，过点P作⊙O的另一条切线交⊙O于点E，连接BE，若∠CBE＝20°，求∠ABE和∠APE的大小．第9题图解：(Ⅰ)如解图①，连接AC，∵四边形ABCD是正方形，∴∠ADC＝90°，∠CAD＝45°，∴AC是⊙O的直径．∵AP是⊙O的切线，∴∠OAP＝90°.∴∠PAD＝90°－∠CAD＝45°.∵∠ADP＝∠ADC＝90°，∴∠P＝∠PAD＝45°；(Ⅱ)如解图②，连接AC、AE、CE、OE，11∴∠CAE＝∠CBE＝20°.∵PA、PE是⊙O的切线，OA＝OE，∴∠OAP＝∠OEP＝90°，∠AEO＝∠CAE.∴∠AOE＝180°－2∠CAE＝140°，∠PAE＝∠PEA＝90°－20°＝70°.∴∠ABE＝12∠AOE＝70°，∠APE＝180°－2∠PAE＝40°.图①图②第9题解图10.已知⊙O上两个定点A，B和两个动点C，D，AC与BD交于点E.(Ⅰ)如图①，若AB︵＝BC︵，AD是⊙O的直径，求证：AD·AC＝2BD·BC；(Ⅱ)如图②，若AC⊥BD，点O到AD的距离为2，求BC的长．第10题图(Ⅰ)证明：如解图①，连接OB交AC于点F∵AB︵＝BC︵，∴∠BAC＝∠ADB＝∠ACB，OB⊥AC，且AF＝CF＝12AC.又∵AD为⊙O的直径，∴∠ABD＝90°，又∵∠CFB＝90°.∴△CBF∽△DAB.∴CFBD＝BCAD，故CF·AD＝BD·BC.∴AD·AC＝2BD·BC；(Ⅱ)解：如解图②，连接AO并延长交⊙O于点F，连接DF，12∴AF为⊙O的直径，∴∠ADF＝90°，过O作OH⊥AD于点H，∴AH＝DH，∵AO＝OF，∴OH∥DF，DF＝2OH＝4，∵AC⊥BD，∴∠AEB＝∠ADF＝90°，∵∠ABD＝∠F，∴△ABE∽△AFD，∴∠BAE＝∠DAF.∴BC︵＝DF︵.∴BC＝DF＝4.图①图②第10题解图