12.4 第二课时 多项式除以单项式

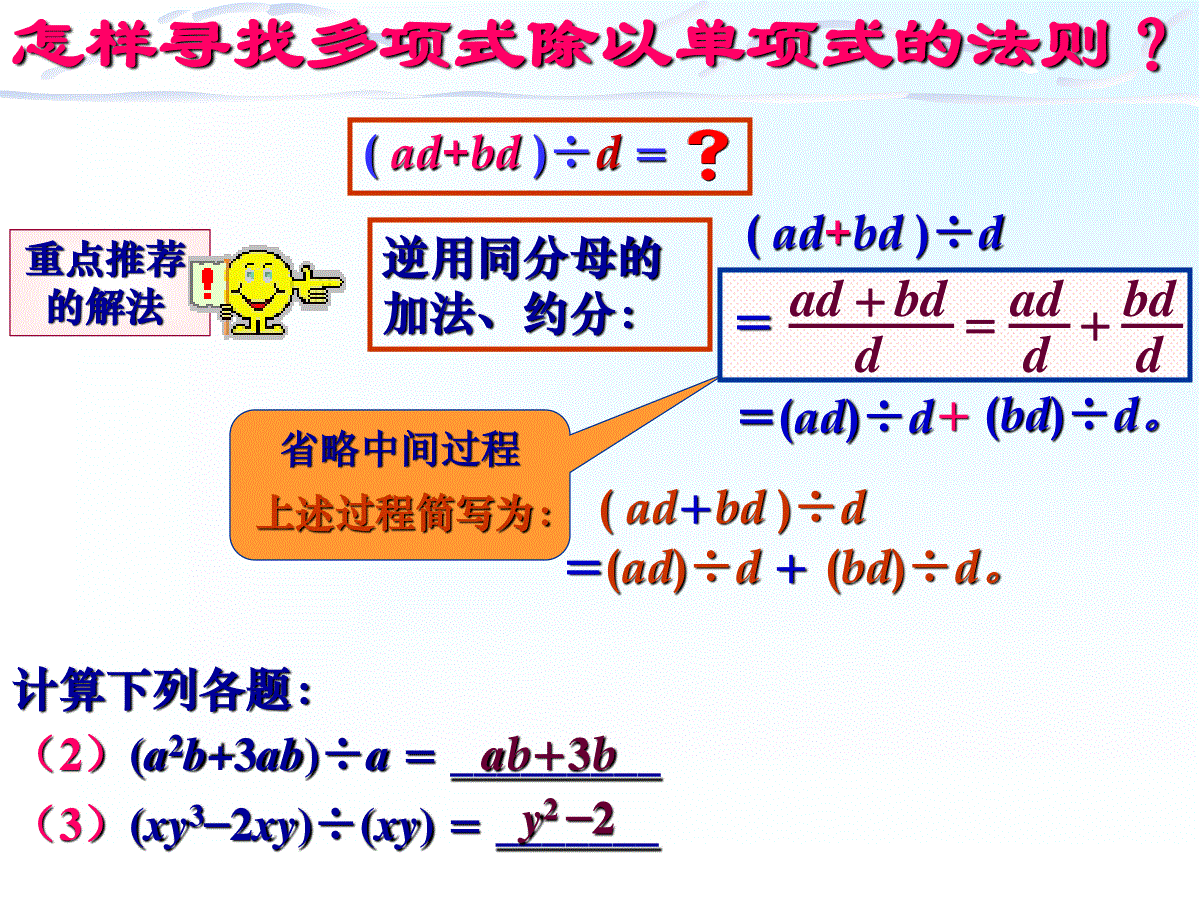
北师大七年级(下)《数学》(华东师大.八年级上册)3a3b2c5ac8(a+b)4–3ab2c回顾与思考回顾&思考☞单项式相除1、系数2、同底数幂3、只在被除式里的幂相除；相除；不变；（1）–12a5b3c÷(–4a2b)=（2）(–5a2b)2÷5a3b2=（3）4(a+b)7÷(a+b)3=21（4）(–3ab2c)3÷(–3ab2c)2=练一练怎样寻找多项式除以单项式的法则？不妨从最简的多项式除以单项式人手，提示:a+b理由(ad+bd)÷d=a+b用逆运算：ad+bd=d•()a+b提取括号内的公因式、约分dbdaddddbaddd逆用同分母的加法、约分：dbdaddbddaddd()d（1）(ad+bd)÷d=__________（2）(a2b+3ab)÷a=_________（3）(xy3–2xy)÷(xy)=_______你能计算下列各题？说说你的理由。怎样寻找多项式除以单项式的法则？(ad+bd)÷d=逆用同分母的加法、约分：重点推荐的解法(ad+bd)÷d=(ad)÷d+(bd)÷d。省略中间过程dbddaddbdad=上述过程简写为：(ad+bd)÷d=(ad)÷d+(bd)÷d。计算下列各题：（2）(a2b+3ab)÷a=_________（3）(xy3–2xy)÷(xy)=_______ab+3by2–2你找到了多项式除以单项式的规律吗？议一议(ad+bd)÷d=(ad)÷d+(bd)÷d。多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加。多项式除以单项式的法则注：1法则只用于多项式除以单项式，不能类比单项式除多单项式。2.商的项数与多项的项数相同。3步骤：1.分清多项式中的项（每一项包括前面的符号）2.每一项3.商相加。（先定符号，后定值）单项式不能漏注：1法则只用于多项式除以单项式，不能类比单项式除多单项式。2.商的项数与多项的项数相同。3步骤：1.分清多项式中的项（每一项包括前面的符号）2.每一项3.商相加。（先定符号，后定值）单项式不能漏例题解析例3计算：；）（；）（)3()61527(2)2()86(123aaaabbab。）（；）（)21()213(4)3()69(32222xyxyxyyxxyxyyx（4）原式=yx23在计算单项式除以单项式时，要注意什么？先定商的符号；注意把除式(后的式子)添括号;3a+4，（1）（2）2592aa（3）yx23解：)21(xy)21(32xyyx2xy)21(xy)21(2xyxyxy21)21(xy)21(21xyxy=x6y2.11、计算：接综合练习随堂练习随堂练习（1）yyxy3（2）mmcmbma（3）dcdcdc233226=3x+1=a+b+c2213cdyx7374（4）xyxyyx73422(5)2)(2)()(22baba(6)yyxyxyx42222abx+2y=[x2+4xy+4y2–(x2–4y2)]=[4xy+8y2]m平方+m-1输出2、任意给一个非零数，mmmm12=m÷m按下列程序计算下去，输入m写出输出结果.1、系数相除；2、同底数幂相除；3、只在被除式里的幂不变。先把这个多项式的每一项分别除以单项式，再把所得的商相加。本节课你的收获是什么？单项式相除多项式除以单项式作业作业（1）多项式mnnnaaa22212它除以，其商式应是（）项式，na商式为mmnnnaaa21m2612131xyyxn6510yx(3)1819123nxxy()=1(2)42232322yyxxxxy2综合练习一共有（）项接作业选讲