2020高考各地数学模拟试题精选——立体几何解答题

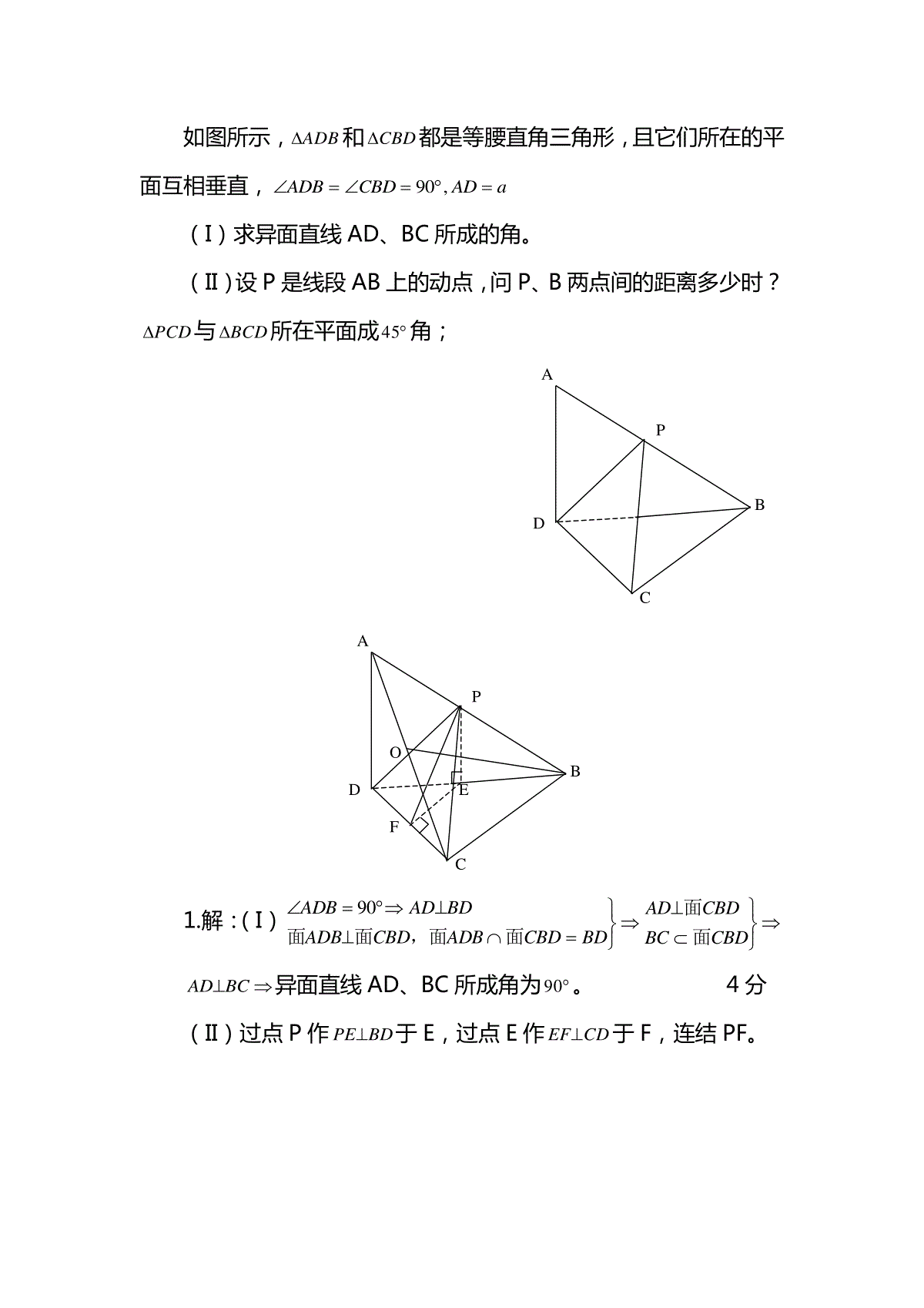
如图所示，ADB和CBD都是等腰直角三角形，且它们所在的平面互相垂直，ADBCBDADa90,（I）求异面直线AD、BC所成的角。（II）设P是线段AB上的动点，问P、B两点间的距离多少时？PCD与BCD所在平面成45角；APBDCAPOBDEFC1.解：（I）ADBADBDADBCBDADBCBDBDADCBDBCCBD90面面，面面面面ADBC异面直线AD、BC所成角为90。4分（II）过点P作PEBD于E，过点E作EFCD于F，连结PF。面面面面面是在面内射影是二面角的平面角ADBCBDADBCBDBDPEBDPECBDCDEFEFPFCBDCDPFEFCDPFEPCDB8分PFE45。设PBx，则在RtPEB中，PEBEx22，DEax22在RtDFE中，EFDEax222212在RtPEF中，EFPEaxxxa，，22122222()11分即P、B两点间距离为()22a时，PCD与BCD所在平面成45角。12分2.【哈师大附中、东北师大附中、辽宁省实验中学2020模拟年高三第二次联合考试数学试卷（理科）】已知直三棱柱ABCABC111中，ABC90，AB=BC=a，AAAB12，M为CC1上的点。（1）当M在CC1上的什么位置时，BM1与平面AACC11所成的角为30；（2）在（1）的条件下求B到平面AMB1的距离。CMC1BB1AA12.解：（1）取ACNBNNM111111的中点，连结，面面面面面ACCAABCACCAABCACBCABBNACBNACCA111111111111111111111111则为与面所成的角BMNBMACCA11111…………3分设，，CMxBNaBMNBNBMaxa1111111122222212sin解得，则xaCMCC1112MCC为的中点…………分16（2）取BBKMKMKABBA111的中点，连结，则面过作，连，过作KKSABMSKKHMS1CMC1BB1AA1SKHN1KHKAMB的长为到面1的距离，由BBBK112，则B到面AMB1的距离为K到面AMB1的距离的2倍…………9分在中，，，··RtMKSMKaKSaKHKSMKMSaaaa556566KABMaBAMBa到面的距离为到面的距离为…………分11666312另法一：利用体积相等，VVBAMBaBAMBMABB11163可求得：到面的距离为另法二：可利用面ABMBMB面13．如图已知四棱锥P—ABCD，PA⊥平面ABCD，底面ABCD为直角梯形，∠A=90°且AB//CD，AB=21CD.（I）点F在线段PC上运动，且设问当,||||FCPF为何值时，BF//平面PAD？并证明你的结论；（Ⅱ）二面角F—CD—B为45°，求二面角B—PC—D的大小；（Ⅲ）在（Ⅱ）的条件下，若AD=2，CD=3，求点A到平面PBC的距离.3．解：（1）当.//,1PADBF平面时（1分）证明：取PD中点E，则EF//CD，且,21//,21CDABCDABCDEF且又∴四边形ABFE为平行四边形.（3分）∴BF//AE.又AE平面PAD∴BF//平面PAD（4分）（2）PA平面ABCD，PDAPDCDADCD即是二面角的平面角45PDA（5分）PAD为等腰直角三角形，,,,CDAEADCDPDAEAE平面PCD又BF//AE，BF平面PCD.BF平面PBC，∴平面PCD⊥平面PBC，即二面角B—PC—D的大小为90°.（8分）（3）在平面PCD内作EH⊥PC于点H，由平面PCD⊥平面PBC且平面PCD平面PBC=PC知：EH⊥平面PBC.（9分）在17,22CDPDPCPCDRt中，在23,217,2,,EFPFPEEFPEPFEHPEFRt将中代入得：.17343EH即点E到平面PBC的距离为.17343（11分）又,//,//PBCAEBFAE平面点A到平面PBC的距离为.17343（12分）4．【北京四中2020模拟年数学第一次统测（理科）】如图，分别是正方体的棱上的点.（1）若，求证：无论点在上如何移动，总有；（２）若，且平面，求二面角的大小.4.（I）证法一：连AC、BD，则BD⊥AC，∵，∴MN//AC，∴BD⊥MN.又∵DD1⊥平面ABCD，∴DD1⊥MN，∴MN⊥平面BDD1.∵无论点P在DD1上如何移动，总有BP平面BDD1，故总有MN⊥BP.证法二：连结AC、BD，则AC⊥BD.∵，∴MN//AC，∴MN⊥BD，又PD⊥平面ABCD，由三垂线定理得：MN⊥PB.（II）解法一：过P作PG⊥C1C交CC1于G，连BG交B1N于O1，∵PB⊥平面B1MN，∴PB⊥B1N.又∵PG⊥平面B1BCC1，∴BG⊥B1N，∴ΔBB1N≌ΔBCG，∴BN=CG，NC=GC1，∴BN∶NC=DP∶PD1=2∶1.同理BM∶MA=DP∶PD1=2∶1.设AB=3a,则BN=2a,∴,,连MO1，∵AB⊥平面B1BCC1，∴MO1⊥B1N，∵∠MO1B就是二面角M-B1N-B的平面角，，∴.解法二：设BD与MN相交于F，连结B1F，∵PB⊥平面MNB1，∴PB⊥B1F，PB⊥MN，∴在对角面BB1D1D内，ΔPBD∽ΔBB1F，设BB1=DD1=3，则PD=2，，∴，即，故.∵MN⊥PB，由三垂线定理得MN⊥BD，MN//AC，MN=2BF=，BN=2，.设二面角B-B1N-M的平面角为α，则，.5．【2020模拟年高考重庆地区信息试卷数学试题】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且(01.)AEAFACAD（Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；（Ⅱ）当λ为何值时，平面BEF⊥平面ACD？5．（1）∵AB⊥平面BCD，∴AB⊥CD，∵CD⊥BC且AB∩BC=B，∴CD⊥平面ABC.3分又),10(ADAFACAE∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF,∴不论λ为何值恒有平面BEF⊥平面ABC.6分（2）由（Ⅰ）知，BE⊥EF，又平面BEF⊥平面ACD，∴BE⊥平面ACD，∴BE⊥AC.8分∵BC=CD=1，∠BCD=90°，∠ADB=60°，∴,660tan2,2ABBD10分,722BCABAC由AB2=AE·AC得,76,76ACAEAE故当76时，平面BEF⊥平面ACD.12分19．湖北省部分重点中学2020模拟年春季期中联考如图，ABCD是矩形，PA⊥平面ABCD，PA＝AD＝a，AB＝2a，E是线段PD上的点，F是线段AB上的点，且)λ(λFABFEDPE0．(I)当21λ时，求直线EF与平面ABCD所成角的正弦值：(Ⅱ)是否存在实数λ，使异面直线EF与CD所成角为60°?若存在，试求出λ的值；若不存在，请说明理由．5.（1）13132EFEMEFMsin(2)存在实数λ，其值为5