当前位置:首页 > 建筑/环境 > 工程监理 > 第三章--中心对称图形期末复习
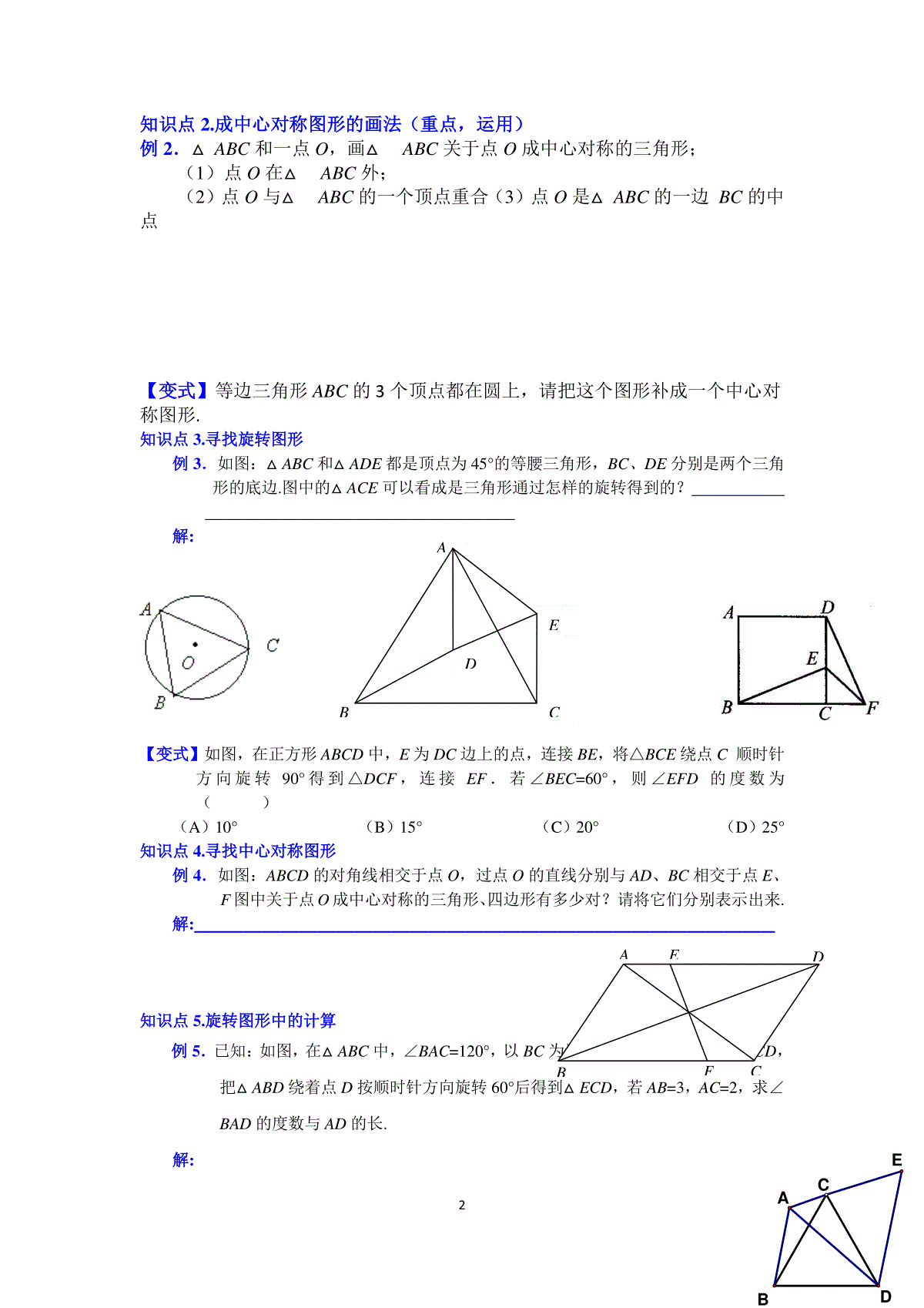
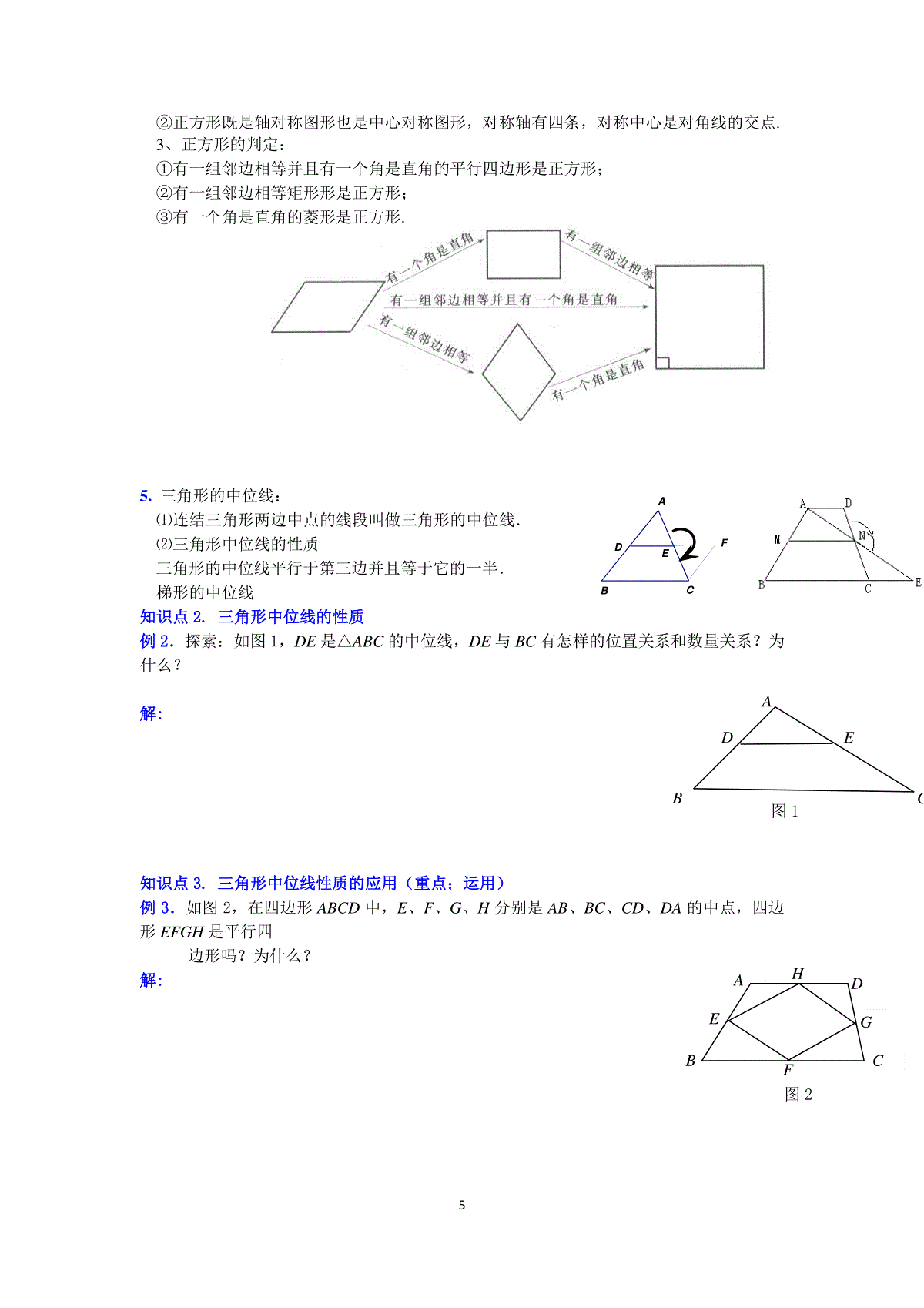
1ABCO第三章中心对称图形(一)期末复习1.图形的旋转:在平面内,___________________________________,这样的图形运动称为图形的旋转,这个定点称为_____________,旋转的角度称为_____________.①旋转前、后的图形全等.②对应点到旋转中心的距离相等.③每一对对应点与旋转中心的连线所成的角彼此相等.2.中心对称.把一个图形绕着某一个点旋转180°,_____________________,那么称这两个图形关于这一点对称.也称这两个图形成中心对称,这个点叫做_____________,两个图形中的对应点叫做_____________.注意:①中心对称是旋转的一种特例,因此,成中心对称的两个图形具有旋转图形的一切性质.②成中心对称的2个图形,对称点的连线都经过对称中心,并且被对称中心平分.3.中心对称图形.把一个平面图形绕着某一点旋转180°,如果旋转后的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.中心对称图形上的每一对对应点所连成的线段都被对称中心______________.知识点1.图形旋转的画法例1.已知线段AB和点O按下面的方法画出线段AB绕点O按逆时针方向旋转100°后的图形解:【变式】1.分别在右图中,画出ABC以O点为中心顺时针旋转60后的旋转图形.2.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是()A.(1,1)B.(1,2)C.(1,3)D.(1,4)3.画出线段AB绕点O旋转后,线段AB的对应线段是A′B′,你能确定旋转中心点O的位置吗?ABAB’′2知识点2.成中心对称图形的画法(重点,运用)例2.△ABC和一点O,画△ABC关于点O成中心对称的三角形;(1)点O在△ABC外;(2)点O与△ABC的一个顶点重合(3)点O是△ABC的一边BC的中点【变式】等边三角形ABC的3个顶点都在圆上,请把这个图形补成一个中心对称图形.知识点3.寻找旋转图形例3.如图:△ABC和△ADE都是顶点为45°的等腰三角形,BC、DE分别是两个三角形的底边.图中的△ACE可以看成是三角形通过怎样的旋转得到的?解:【变式】如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF.若∠BEC=60°,则∠EFD的度数为()(A)10°(B)15°(C)20°(D)25°知识点4.寻找中心对称图形例4.如图:ABCD的对角线相交于点O,过点O的直线分别与AD、BC相交于点E、F图中关于点O成中心对称的三角形、四边形有多少对?请将它们分别表示出来.解:知识点5.旋转图形中的计算例5.已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长.解:CBDAECBDEAAEDBFC34.如图,在正方形ABCD中,点E是AD的中点,点F是BA延长线上一点,AF=21AB,△ABE可以通过绕A点逆时针旋转到△ADF的位置,则旋转的最小角度为.5.如图是一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线(保留作图痕迹),简要说明理由.6.如图,一块方角形的木板,能不能在图中画出一条直线,将其分成面积相等的两部分,(不写作法,在图中直接画出,保留痕迹),试试看,并尽可能多的把你的想法画出来.7.如图,四边形ABCD中,AD∥BC,DF=CF,连结AF并延长交BC延长线于点E.(1)图中哪两个三角形可以通过怎样的旋转而相互得到?(2)四边形ABCD的面积与图中哪个三角形的面积相等?(3)若AB=AD+BC,∠B=70°,试求∠DAF的度数.如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转,DE,DF分别交线段..AC于点M,K.(1)观察:①如图2、图3,当∠CDF=0°或60°时,AM+CK_______MK(填“”,“”或“=”).②如图4,当∠CDF=30°时,AM+CK___MK(只填“”或“”).(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.(3)如果222AMCKMK,请直接写出∠CDF的度数和AMMK的值.(M)EKDCABFMEKDCABFMEKDCABFLMEDCAB(F,K)HABDCGEF12341.平行四边形(1)平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.记作:□ABCD,读作平行四边形ABCD.平行四边形是中心对称图形,对角线的交点是它的对称中心.(2)平行四边形的性质:________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________(3)平行四边形的判定:________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________2.矩形(1)矩形的定义:有一个角是直角的平行四边形叫做矩形,通常也叫长方形.(2)矩形的性质:________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________(3)矩形的判定:________________________________________________________________________________________________________________________________________________________________________________________________3.菱形(1)菱形的定义:有一组邻边相等的平行四边形叫做菱形.(2)菱形的性质:________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________(3)菱形的判定:________________________________________________________________________________________________________________________________________________________________________________________________(4)菱形的面积:S菱形=21AC·BD4.正方形1、正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.2、正方形的性质:①正方形具有矩形的性质,同时又具有菱形的性质.5②正方形既是轴对称图形也是中心对称图形,对称轴有四条,对称中心是对角线的交点.3、正方形的判定:①有一组邻边相等并且有一个角是直角的平行四边形是正方形;②有一组邻边相等矩形形是正方形;③有一个角是直角的菱形是正方形.5.三角形的中位线:⑴连结三角形两边中点的线段叫做三角形的中位线.⑵三角形中位线的性质三角形的中位线平行于第三边并且等于它的一半.梯形的中位线知识点2.三角形中位线的性质例2.探索:如图1,DE是△ABC的中位线,DE与BC有怎样的位置关系和数量关系?为什么?解:知识点3.三角形中位线性质的应用(重点;运用)例3.如图2,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,四边形EFGH是平行四边形吗?为什么?解:FEDCBAABCDE图1CHFEDBAG图266.四边形的中点四边形原四边形中点四边形任意四边形矩形菱形正方形矩形菱形知识点1.正方形的判定例1.如图:四边形ABCD的对角线相交于点O,且AD∥BC,AD=BC请补充2个条件,使四边形ABCD为正方形,并说明理由.解:知识点2.菱形的性质例2.如图:在菱形ABCD中,∠B=60°,点E、F分别在AB、AD上,且BE=AF.你能说明△ECF是等边三角形吗?解:知识点3.矩形的判定例3.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交外角∠DCA的平分线于点F.(1)猜想线段OE与线段OF的关系,并说明理由.(2)当点O运动到何处时,四边形AECF是矩形?为什么?ADBCFEABCOD7解:知识点4.正方形、矩形的性质例4.如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB,(1)试猜测DE与FG关系如何?并说明理由.(2)如果正方形ABCD的边长为4㎝,求四边形BGEF的周长解:知识点5.三角形中位线的性质例5.如图,等腰梯形ABCD对角线交于点O,点E、F、G分别是AO、BO、DC的中点,∠AOD=60°,试说明△EFG是等边三角形.解:1.在平行四边形、矩形、菱形、正方形、等腰梯形、圆这6种图形中,既是轴对称图形又是中心对称图形的有(A)6种(B)5种(C)4种(D)3种2.已知△ABC的中线BE、CF相交于点O,M、N分别是OB、OC的中点,则四边形EFMN是_______形.3.矩形ABCD中,AC、BD相交于点O,E为矩形ABCD外一点,若AE⊥CE,求证BE⊥DE.OFEABCDGFBAEGCDAEBCDO8AEDCBEBOFCDA5.△ABC中E是AB的中点,CD平分∠ACD,AD⊥CD与点D,求证:DE=21(BC-AC).6.如图:AE是正方形ABCD中∠BAC的平分线,AE分别交BD、BC于F、E,AC、BD相交于O,求证:OF=21CE.7.如图(1)所示,△ABC是直角三角形,∠C=90°,现将△ABC补成矩形,使△ABC的2个顶点为矩形一边的2个端点,第三个顶点落在矩形这一边的对边上,那么符合要求的矩形可以画出2个,如图(2)所示,这2个矩形的面积和周长都分别相等吗?98.(2010·贵州毕节)如图,



 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 sophia77
sophia77
共143篇文档
格式: doc
大小: 491 KB
时间: 2020-05-28
本文标题:第三章--中心对称图形期末复习
链接地址:https://www.777doc.com/doc-5602557 .html