当前位置:首页 > 幼儿/小学教育 > 小学教育 > 平行四边形创新题赏析知识归纳初中数学人教版八年级下册教学资源
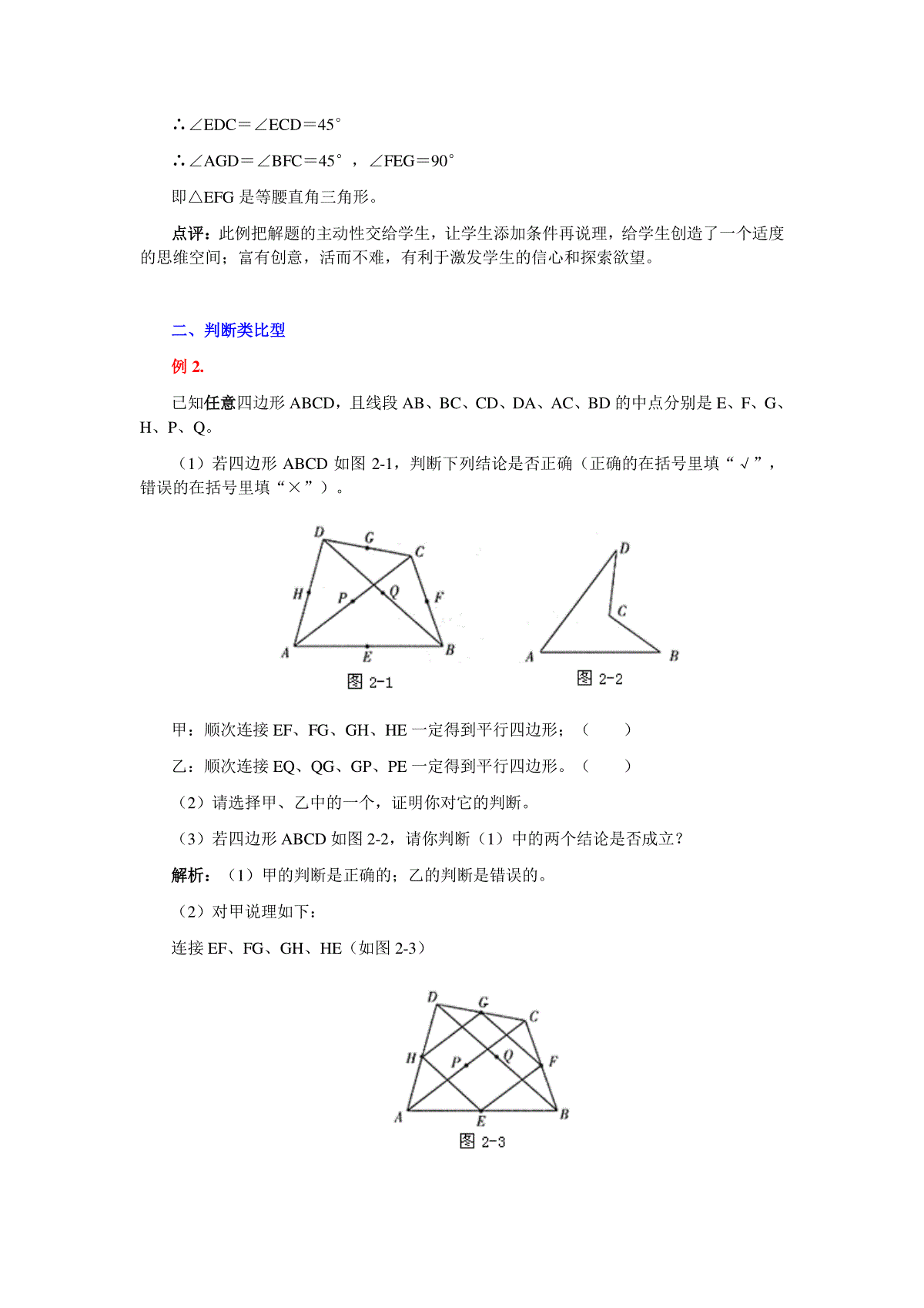
平行四边形创新题赏析平行四边形部分是初中数学的重点内容,在各地中考试卷中都占有一定的分量。随着课程改革的进一步深入,出现了许多构思新、重素质、考能力的创新题型,令人耳目一新;它对培养和考查学生的发散能力和综合能力大有裨益。现例举中考题几例并加以归类浅析,希望对同学们有所启发。一、补充说理型例1.如图1,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G。(1)求证:AF=GB;(2)请你在已知条件的基础上再添加一个条件,使得△EFG为等腰直角三角形,并说明理由。图1解析:(1)∵四边形ABCD是平行四边形∴AB∥CD,∴∠AGD=∠CDG又∵DG是∠ADC的平分线∴∠ADG=∠GDC∴∠AGD=∠ADG∴AD=AG同理可得:BF=BC在平行四边形ABCD中,AD=BC∴AG=BF∴AF=GB(2)可以添加条件∠ADC=90°或四边形ABCD是矩形说理如下:∵四边形ABCD是矩形∴∠ADC=∠BCD=90°又DG、CF平分∠ADC和∠BCD∴∠EDC=∠ECD=45°∴∠AGD=∠BFC=45°,∠FEG=90°即△EFG是等腰直角三角形。点评:此例把解题的主动性交给学生,让学生添加条件再说理,给学生创造了一个适度的思维空间;富有创意,活而不难,有利于激发学生的信心和探索欲望。二、判断类比型例2.已知任意四边形ABCD,且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q。(1)若四边形ABCD如图2-1,判断下列结论是否正确(正确的在括号里填“√”,错误的在括号里填“×”)。甲:顺次连接EF、FG、GH、HE一定得到平行四边形;()乙:顺次连接EQ、QG、GP、PE一定得到平行四边形。()(2)请选择甲、乙中的一个,证明你对它的判断。(3)若四边形ABCD如图2-2,请你判断(1)中的两个结论是否成立?解析:(1)甲的判断是正确的;乙的判断是错误的。(2)对甲说理如下:连接EF、FG、GH、HE(如图2-3)∵E、F分别是AB、BC的中点∴EF是△ABC的中位线∴∥,EFACEFAC12同理,HG∥ACHGAC12∴EF∥HG,EF=HG∴四边形EFGH是平行四边形对乙可举反例说明:如图2-4,在矩形ABCD中,顺次连接EQ、QG、GP、PE得到一条线段,而不是一个平行四边形。(3)对图2-2,类似于(1)中的结论甲、乙都成立。点评:此例通过设计问题串,让学生经历判断、归纳,从而建立认识,再作判断;体现了新课程下命题者关注学生思维过程的良苦用心。三、猜想证明型例3.已知:如图3,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF。请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可)。图3(1)连接_____________;(2)猜想_____________=_____________;(3)证明解析:连接AF,猜想AF=AE。证明:连接AC,交BD于O∵四边形ABCD是菱形,∴AC⊥BD于O,DO=BO∵DE=BF,∴EO=FO∴AC垂直平分EF∴AF=AE点评:此例要求学生经历探索—猜想—证明的思维过程,这种螺旋上升的结构符合学生的心理特征和认知规律。让考生在试卷上留下思维的痕迹,能创造性地激活学生的思维。四、运动探究型例5.如图4,已知平行四边形ABCD及四边形外一直线l,四个顶点A、B、C、D到直线l的距离分别为a、b、c、d。(1)观察图形,猜想得出a、b、c、d满足怎样的关系式?证明你的结论。(2)现将l向上平移,你得到的结论还一定成立吗?请分情况写出你的结论。解析:(1)acbd证明:连接AC、BD,且AC、BD相交于点O,OO1为点O到l的距离图4∴OO1为直角梯形BBDD11的中位线∴2111OODDBBbd同理:2111OOAACCac∴acbd(2)不一定成立。分别有以下情况:直线l过A点时,cbd;直线l过A点与B点之间时,cabd;直线l过B点时,cad;直线l过B点时与D点之间时,acbd;直线l过D点时,acb;直线l过C点与D点之间时,acbd;直线l过C点时,abd;直线l过C点上方时,acbd。点评:将静态的数学与动态的变化结合起来,给数学以生命,让学生在图形的变化中理解体验变与不变。本题以“平行四边形”、“线”为背景,在“动”中开拓学生视野,拓宽学生的思维空间,在“静”中寻找关系,从而找到解决问题的途径。该题较好地考查了学生观察、分析、判断论证能力和探究创新能力;有利于培养学生严谨的思维习惯和缜密的治学态度。五、图形设计型例5.在△ABC中,借助作图工具可以作出中位线EF,沿着中位线EF一刀剪切后,用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP,剪切线与拼图如图示1,仿上述的方法,按要求完成下列操作设计,并在规定位置画出图示。图示1(1)在△ABC中,增加条件_____________,沿着_____________一刀剪切后可以拼成矩形,剪切线与拼图画在图示2的位置;(2)在△ABC中,增加条件_____________,沿着_____________一刀剪切后可以拼成菱形,剪切线与拼图画在图示3的位置;(3)在△ABC中,增加条件_____________,沿着_____________一刀剪切后可以拼成正方形,剪切线与拼图画在图示4的位置;(4)在△ABC(AB≠AC)中,一刀剪切后也可以拼成等腰梯形,首先要确定剪切线,其操作过程(剪切线的作法)是____________________________然后,沿着剪切线一刀剪切后可以拼成等腰梯形,剪切线与拼图画在图示5的位置。解:(1)方法一:∠B=90°,中位线EF,如图示2-1。方法二:AB=AC,中线(或高)AD,如图示2-2。(2)AB=2BC(或者∠C=90°,∠A=30°),中位线EF,如图示3。(3)方法一:∠B=90°且AB=2BC,中位线EF,如图示4-1。方法二:AB=AC且∠BAC=90°,中线(或高)AD,如图示4-2。(4)方法一:不妨设∠B>∠C,在BC边上取一点D,作∠GDB=∠B交AB于G,过AC的中点E作EF∥GD交BC于F,则EF为剪切线,如图示5-1。方法二:不妨设∠B>∠C,分别取AB、AC的中点D、E,过D、E作BC的垂线,G、H为垂足,在HC上截取HF=GB,连接EF,则EF为剪切线,如图示5-2。方法三:不妨设∠B>∠C,作高AD,在DC上截取DG=DB,连接AG,过AC的中点E作EF∥AG交BC于F,则EF为剪切线,如图示5-2。点评:重视提高动手操作能力和实践能力,是素质教育新课程的切入点。此类题设计新颖,不落俗套,为考生画图操作、类比联想、反思探究提供了自由发挥、自主探究的广阔思维空间;对进一步理解和应用所学知识,发展创新能力、实践能力、操作能力大有裨益;让学生在具体的操作情境中,领悟数学的发展与形成的真谛。初三中考作业本有这样一道题:如图所示,已知四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线有两条,能否做到:____(选填能或不能),请确定裁剪线的位置,并说明拼接方法:若填不能,请简要说明理由.拿到此题,学生们感觉无从下手.仔细分析此题,此题涉及到如何剪,如何拼的问题,因而我作了如下的解题分析.一.寻找解题思路.(1)由于四边形内角和为3600,因而可以将四个内角拼成一个周角,可以进行平面镶嵌.(2)由于拼成的四边形是平行四边形,因而必须注意边长的特殊性,可以取各边的中点.在找到思路的基础上,我们就可动手裁剪--沿对边的中点剪开,分割成四部分.二.如何拼凑是本题的难点,关键是不能将剪下的图形弄乱.拼时以其中一块图形不动,抓相等的边拼在一起,以相临两边的中点为旋转中心将其中两块图形转1800,不相临的第三块图形平移到空缺处.三.如何说明它是平行四边形.(1)必须说明三点共线.可用两角之和为1800.(2)必须说明它是平行四边形.可用角的关系证明两组对边平行.经过以上的分析,裁剪,拼凑,证明,才可完整的完成此题.




 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:平行四边形创新题赏析知识归纳初中数学人教版八年级下册教学资源
链接地址:https://www.777doc.com/doc-5879165 .html