当前位置:首页 > 行业资料 > 能源与动力工程 > key第十一章无穷级数
1第十一章无穷级数§11.1常数项级数的概念和性质内容概要名称主要内容常数项级数1nnu(nu为常数)常数项级数的收敛性若,ssnn则1nnu收敛,(ns:前n项部分和)常数项级数常用的性质1.0nnu,0nnv收敛)(0nnnvu收敛,且000)(nnnnnnnvuvu2.0k则0nnku与0nnu同收同发3.1nnu加入有限项或去掉有限项,不改变级数的敛散性.4.0nnu收敛0limnnu(收敛的必要条件)常用的结论0nnar当1r时收敛其和为ra1,当1r时发散.例题分析★1.已给级数1)12)(12(1nnn,1)写出此级数的前二项1u,2u;2)计算部分和1s,2s;3)计算第n项部分和1s;4)用级数收敛性定义验证这个级数是收敛的,并求其和.知识点:前n项部分和ns,常数项级数的收敛性.2解:1)311)12)(12(11u,531)14)(14(12u2)3111us;)511(21)5131(21)311(2153131212uus3))121121(21)12)(12(1nnnnun)1211(21)121121(21)5131(21)311(2121nnnuuusnn4)21)1211(21limlimnsnnn,1)12)(12(1nnn收敛,其和为21s.★★★2.求常数项级数110aannn之和.知识点:前n项部分和ns.思路:1)1(110nnnnanan利用0nnarra11r解:令12321nnanaas1a则23132nnnananaaas以上两式相减得1221111)1(nnnanaaaasa即)1111(111122nnnanaaaaaas)1111(11111nnanaaaaannslim)111(111aaaa22)1(aa,01nnan22)1(aa,1a.注:利用等比级数0nnarra11r判别级数的收敛性及求1nnu和是常用的方法.★★3.设1nnu收敛,讨论下列级数的敛散性:31);)0001.0(1nnu2)11000nnu;3)11nnu.知识点:常数项级数的收敛性.思路:利用常数项级数的性质.解:1)00001.00001.0lim)0001.0(limnnnnuu1)0001.0(nnu发散.注:0limnnu,则1nnu发散是判别级数发散常用的方法.2)常数项级数的性质:1nnu加入有限项或去掉有限项,不改变级数的敛散性.去掉1nnu前1000项得的级数11000nnu仍收敛3)01limnnu,11nnu发散.课后习题全解习题11-11.写出下列级数的前五项:★(1)1211nnn★(2)1242)12(31nnn★(3)113)1(nnn★(4)1!nnnn解:(1)222225151414131312121111113317552531.(2)1086429753138410548158321.(3)54323131313131.(4)54325!54!43!32!212.写出下列级数的一般项:★(1)675645342312★(2)368277166954413★(3)86426424222xxxxx★(4)97535432aaaa4★★(5)615413211★★(6)4433221721025222xxxx解:(1))3,2,1(1)1(1)1(11nnnnnunnn.(2))3,2,1(!2)1(nnnunn.(3))3,2,1(!)!2()2(64222nnxnxunnn.(4))3,2,1(12)1(12)1(1111nnanaunnnnn.(5))3,2,1(2112nnnun.(6))3,2,1(122nxnunnn.3.根据级数收敛与发散的定义判定下列级数的收敛性:★★(1))122(1nnnn;★(2))15)(45(11161611nn;★★★(3)6sin63sin62sin6sinn.解:(1)nnnnnnnun11121122.121121)11121()231341()121231(nnnnnnsn所以121limnns,原级数收敛.(2))151451(51)15)(45(1nnnnun.)1511(51)151451(51)11161(51)611(51nnnsn所以51limnns,原级数收敛.5(3)6sin62sin6sinnsn,]12)12cos(12)12[cos(12sin216sinkkk)125cos123(cos)123cos12[(cos12sin21ns)]12)12cos(12)12(cos(nn]12)12cos(12[cos12sin21n所以不存在nnslim,原级数发散.注:另解16)36(sin,066sin366kukukk1lim,0lim366kkkkuu所以nnulim不存在,原级数发散.4.判定下列级数的收敛性:★(1)nnn98)1(9898983322★(2)n31121916131★★(3)1)1(3nnnnn★★(4)121cos1nnn★★(5);3122ln1nnnn★★(6)11)1(nnnnnnn解:(1)此为等比级数,因公比98q,且1q,故此级数收敛于179981111q(2)级数的一般项:nun131,由调和级数11nn发散和级数的性质,知题设级数发散.(3)03)11(3lim)1(3limlimennnunnnnnnn原级数发散.(4)02121lim1cos1limlim222nnnnunnnn,原级数发散.6(5)1131,22lnnnnnn均为等比级数且公比分别为131122ln21q,q1131,22lnnnnnn均收敛,故原级数nnnn3122ln1收敛.(6)01)11(lim)1(limlim211nnnnnnnnnnnnnnu.原级数发散.★★5.求级数1)2)(1(1nnnn的和.解:)21121(21)2)(1(1nnnnnnun.41slim)211121(21)21121121221(21)21121(21)514231(21)413221(21)31221(21nnsnnnnnnnnsn★★★6.求常数项级数13nnn之和.解:nnns333323132,132334333213nnnsnnnns33131311212nnn3311311(上两式相减)43)3311311(lim21slim3nn1nnnnnnn.★★7.设级数1nna的前n项和为nnnsn111,求级数的一般项na及和s.解:1111111nnnsn,nnnssannn12112117且2ln1111111n1limslim10dxxnnnsnnn.★★★★8.利用柯西审敛原理判别下列级数的收敛性:(1)11)1(nnn;(2)12sinnnnx;(3)nnn1cos11.解:(1)对于任意自然数p,因为)()111()3121(11)(1)5141()3121(111)1(2111)1(2)1(1)1(113221为奇数为偶数ppnpnnnnppnnnnnnpnnnpnnnuuuppnnnpnnn11n(令,11n解得11n)故,0不妨设,0]11[,1N当Nn时,对于任意自然数p,都有1121nuuupnnn由柯西审敛原理,知所给级数收敛.(2)对于任意自然数p,因为npnpnpnnnpnnnpnnnxpnxnxnxpnxnxnuuu21)211(21)212121(212)sin(2)2sin(2)1sin(2)sin(2)2sin(2)1sin(2212121故,0不妨设,0]2lnln[,1N当Nn时,对于任意自然数p,都有npnnnuuu2121由柯西审敛原理,知所给级数收敛.(3)11cos1cos,nnn有,因为8nnnnnnnnuuunnnn1cos121cos2111cos1121nnnnnnn(1cos211cos211cos21项))2(21cos211cos21nn故取,21cos210对于任意npNn2,,使得021pnnnuuu由柯西审敛原理,知所给级数发散.提高题1.判定下列级数的收敛性:★★1)1)151(nnn;★★2)1)cos(2nnn;★★★★3)11)11(2nnnen;★★★★4)1)1(!nnnenn.解:1)151nn收敛,11nn发散,1)151(nnn发散.2)nunnnn2)1()cos(20limnnu1)cos(2nnn发散.3)nnulimxxxxxxxnnneexen)11ln(222lim1)11(lim1)11(lim01212111lim2111lim)1ln(lim0020eeeexttttttttttt11)11(2nnnen发散.4)nnuu1enennennennnnnnnnn11111)111(1)2()1()1(!)2()!1(9由数列nn)11(单调递增趋于e知:enn)11(11nnuu即11uuunn,0limnnu,12)1(!nnenn发散.2.求下列级数的和.★★1)122391nnn;★★★★2)121482arctannnn解:1))1

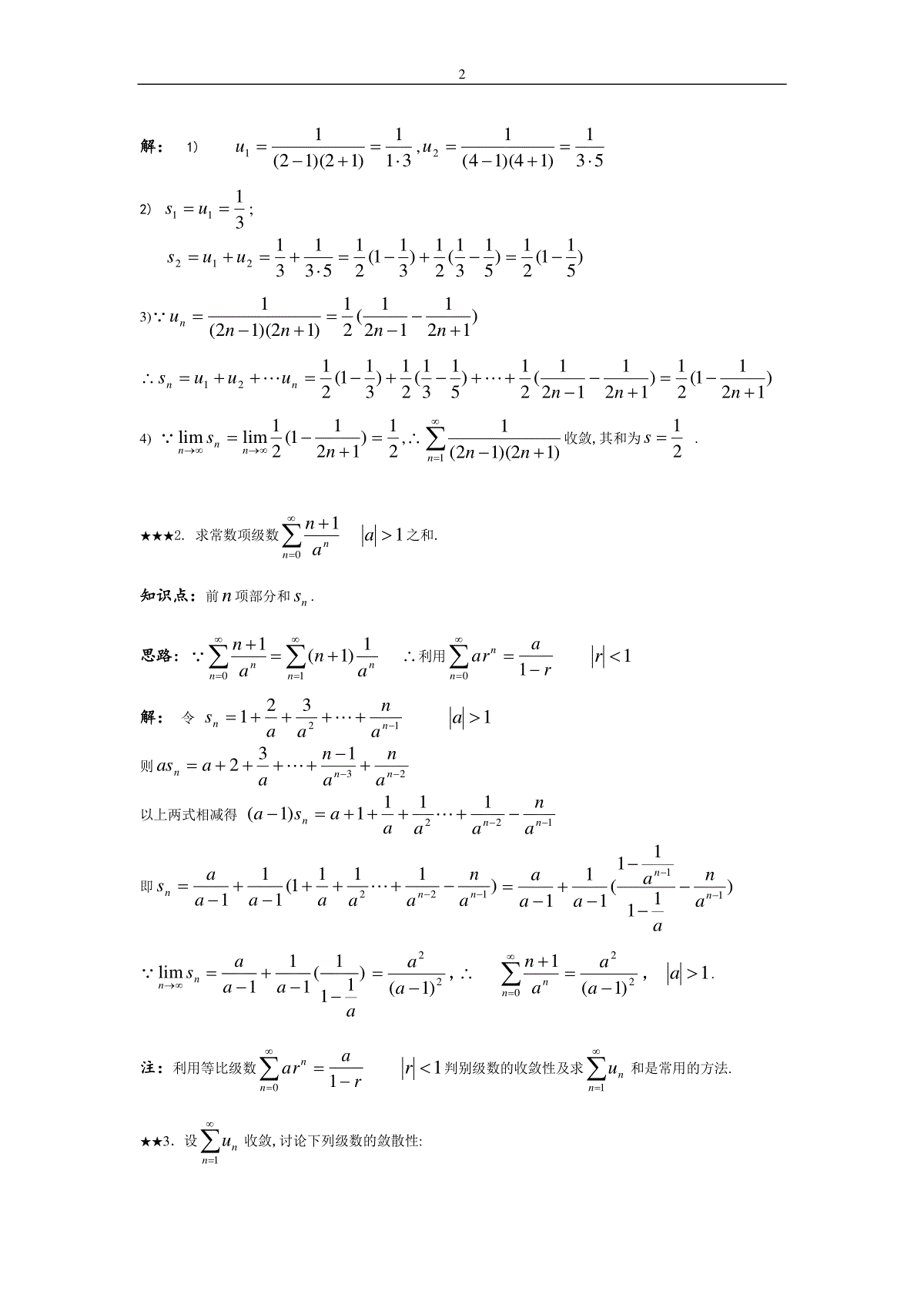

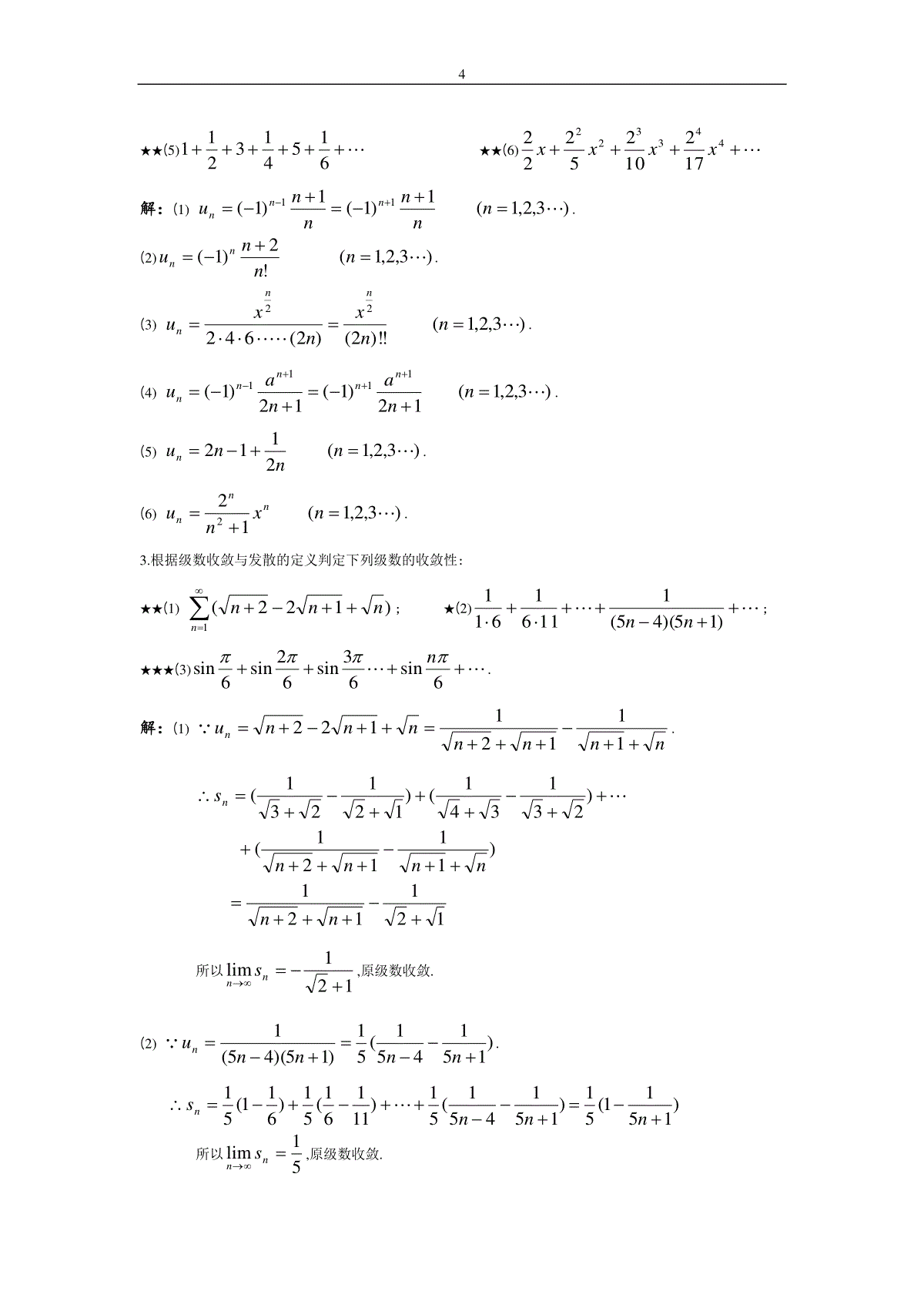
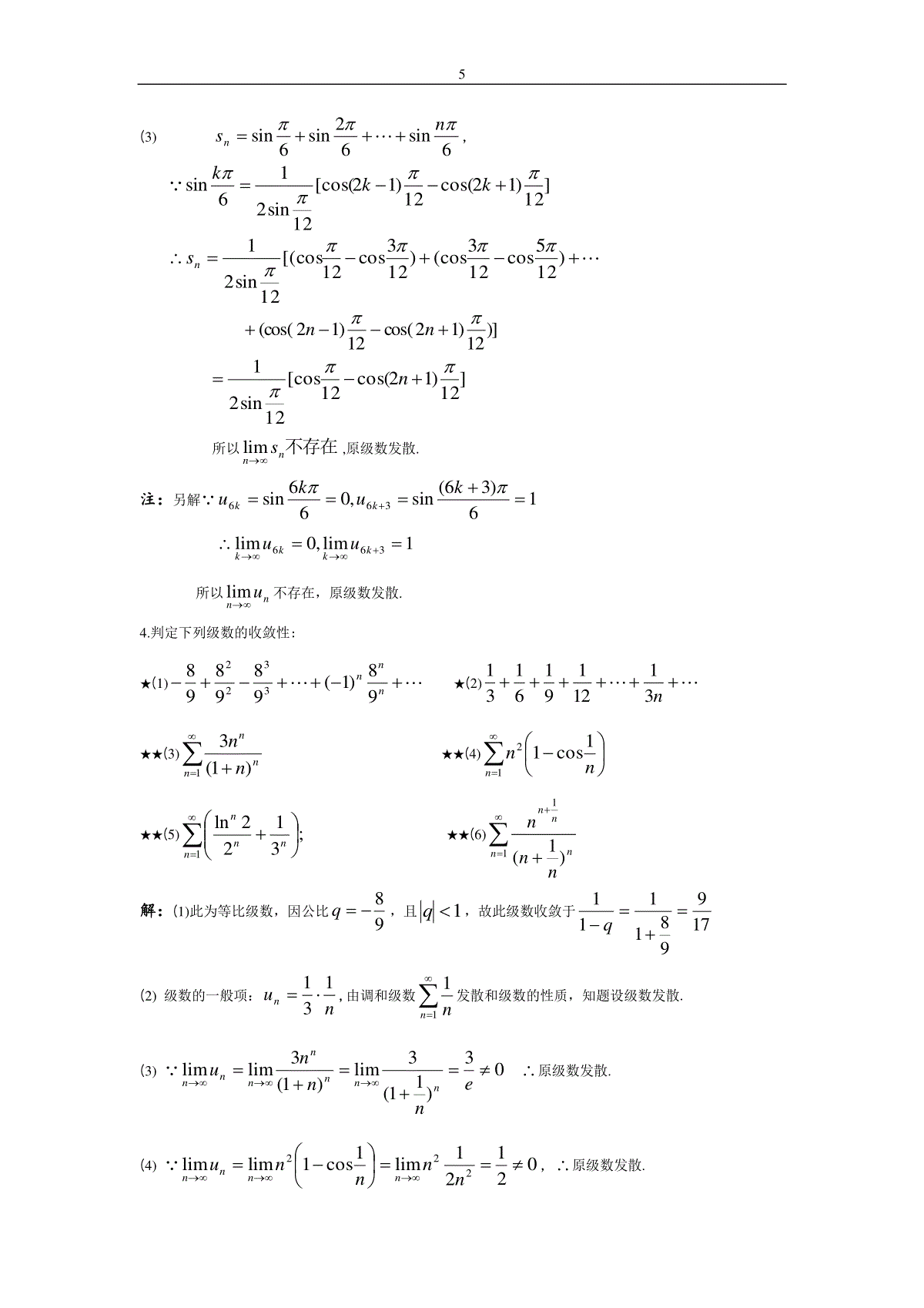
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:key第十一章无穷级数
链接地址:https://www.777doc.com/doc-5935372 .html