轴对称题型讲解与综合练习

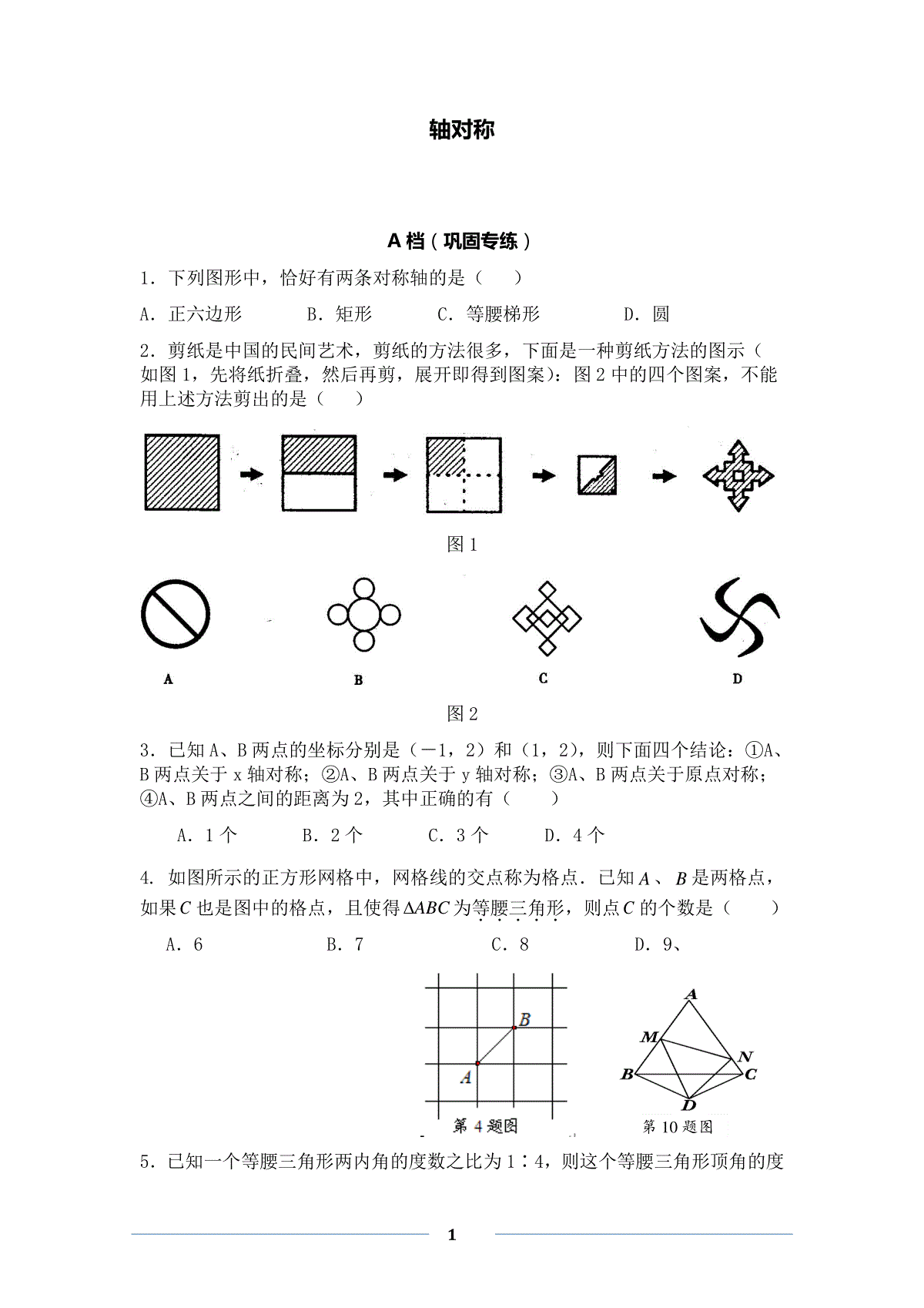
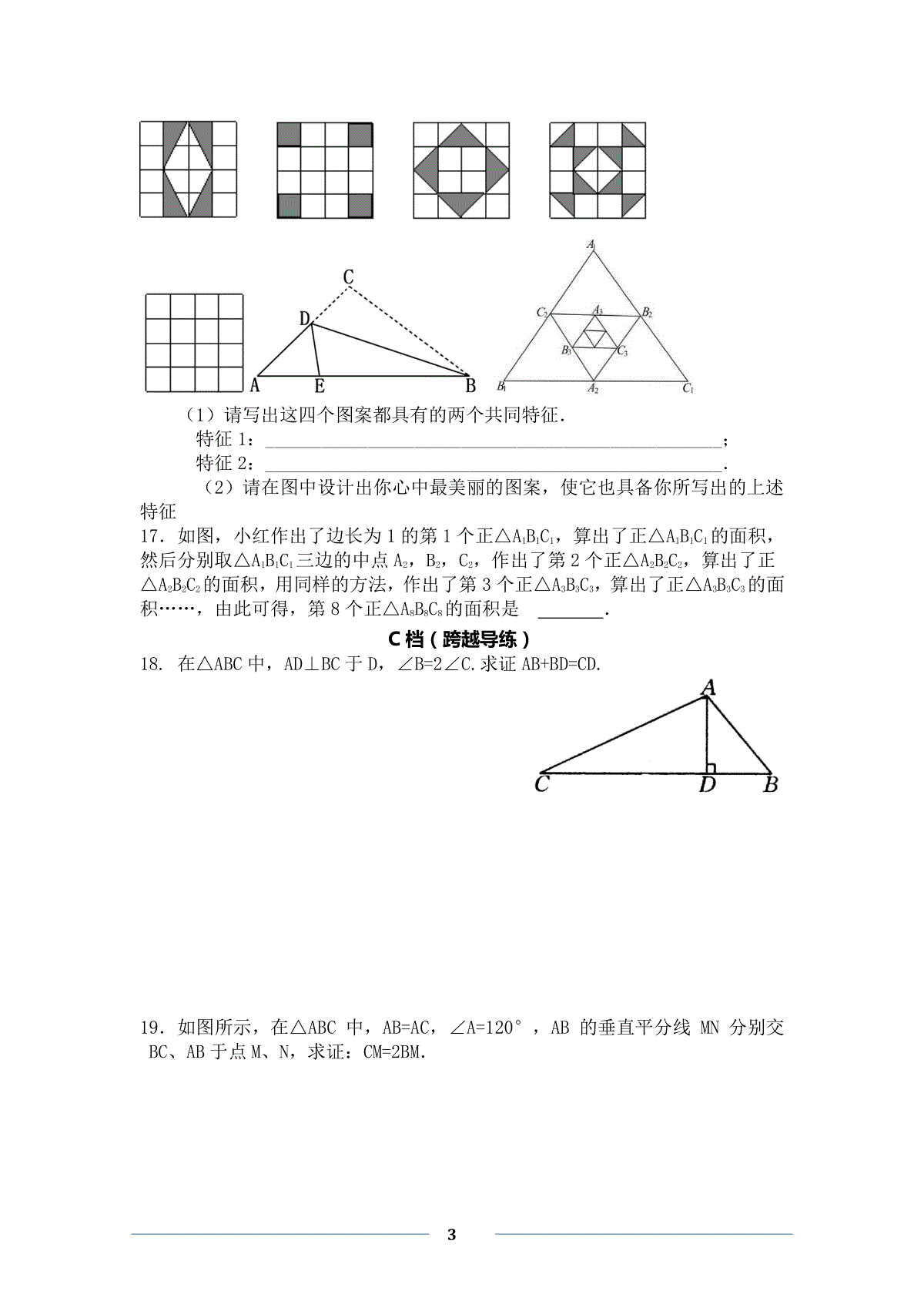
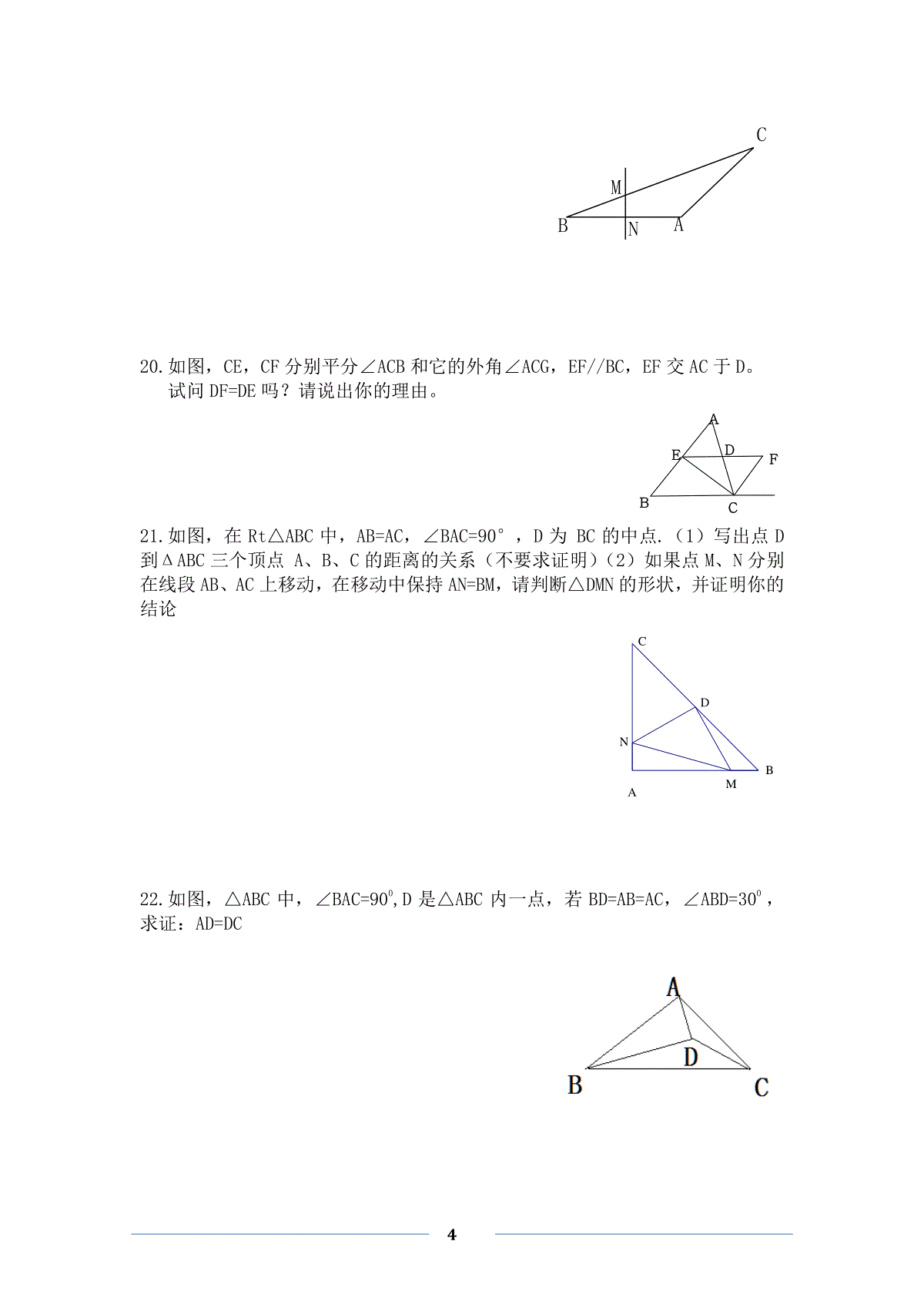
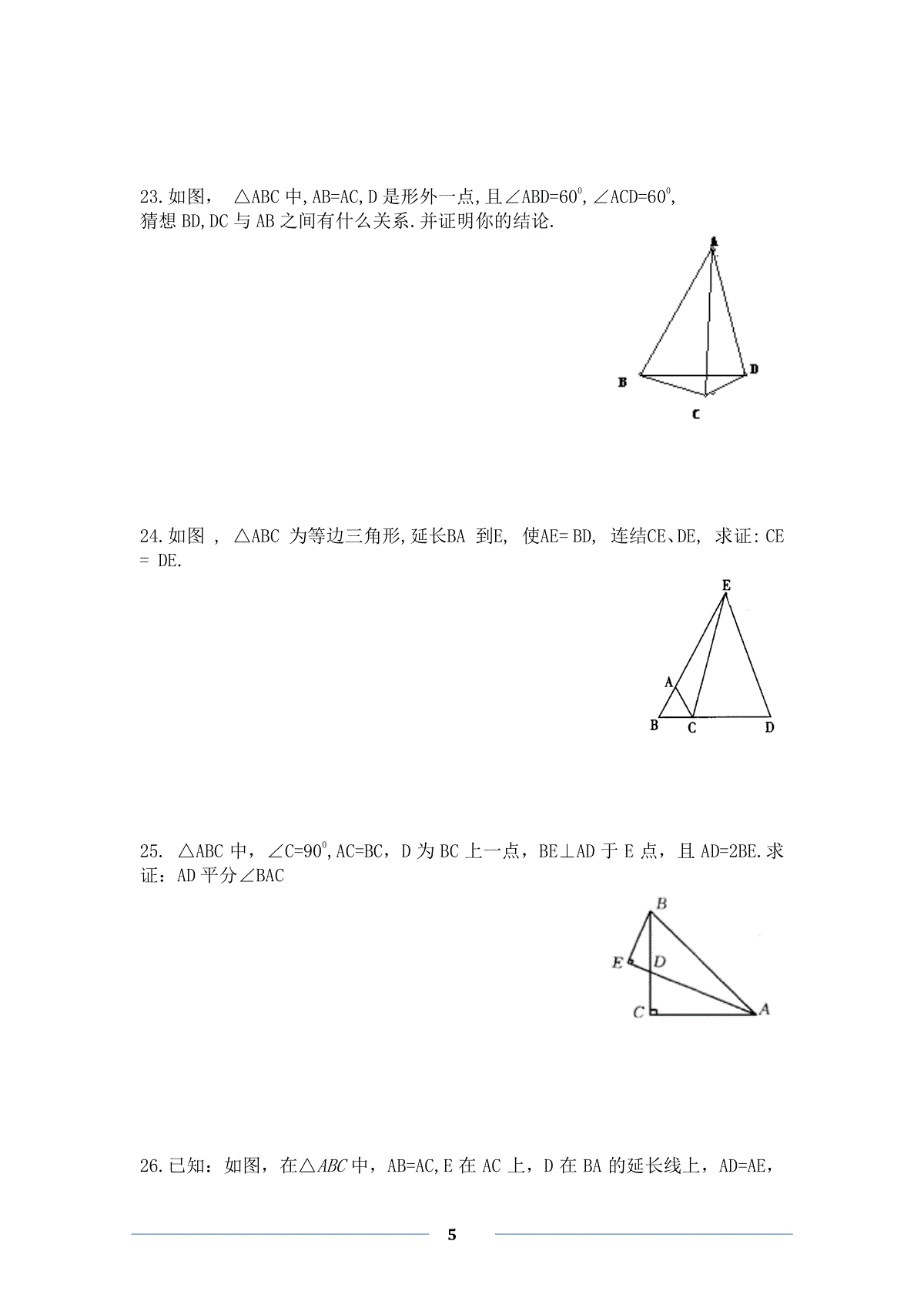
1轴对称A档（巩固专练）1．下列图形中，恰好有两条对称轴的是（）A．正六边形B．矩形C．等腰梯形D．圆2．剪纸是中国的民间艺术，剪纸的方法很多，下面是一种剪纸方法的图示（如图1，先将纸折叠，然后再剪，展开即得到图案）：图2中的四个图案，不能用上述方法剪出的是（）图1图23．已知A、B两点的坐标分别是（－1，2）和（1，2），则下面四个结论：①A、B两点关于x轴对称；②A、B两点关于y轴对称；③A、B两点关于原点对称；④A、B两点之间的距离为2，其中正确的有（）A．1个B．2个C．3个D．4个4.如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得ABC为等腰三角形．．．．．，则点C的个数是（）A．6B．7C．8D．9、5．已知一个等腰三角形两内角的度数之比为1∶4，则这个等腰三角形顶角的度第10题图2数为（）A．200B．1200C．200或1200D．3606.等腰三角形一腰的中线把周长分成33cm和24cm两部分，则它的腰长（）cmA13B、16C、22D、16或227.如图所示，已知△ABC和△DCE均是等边三角形，点B、C、E在同一条直线上，AE与BD交于点O，AE与CD交于点G，AC与BD交于点F，连结OC、FG，则下列结论：①AE＝BD②AG＝BF③FG∥BE④∠BOC＝∠EOC，其中正确结论的个数（）A.1个B.2个C.3个D.4个第7题第8题第9题8.如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′等于（）A．70°B．65°C．50°D．25°9.如图，等腰△ABC中，AB=AC，∠A=20°。线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（）A．80°B．70°C．60°D．50°B档（提升精练）10.如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC＝120°．以D为顶点作一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为．11.已知A(2m+n,2)，B(1,n-m)，若A、B关于x轴对称，则m=，n=．12.已知点M(1-a,2a+2)，若点M关于x轴的对称点在第三象限，则a的取值范围是．13.已知等腰三角形的一个内角为70°，则另外两个内角的度数是．14.如图，三角形纸片ABC，10cm7cm6cmABBCAC，，，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则AED△的周长为______cm．15.如果等腰三角形的三边长均为整数，且它的周长为10cm，那么它的三边长分别为.16.认真观察下图中的4个图中阴影部分构成的图案，回答下列问题：3（1）请写出这四个图案都具有的两个共同特征．特征1：_________________________________________________；特征2：_________________________________________________．（2）请在图中设计出你心中最美丽的图案，使它也具备你所写出的上述特征17．如图，小红作出了边长为1的第1个正△A1B1C1，算出了正△A1B1C1的面积，然后分别取△A1B1C1三边的中点A2，B2，C2，作出了第2个正△A2B2C2，算出了正△A2B2C2的面积，用同样的方法，作出了第3个正△A3B3C3，算出了正△A3B3C3的面积……，由此可得，第8个正△A8B8C8的面积是．C档（跨越导练）18.在△ABC中，AD⊥BC于D，∠B=2∠C.求证AB+BD=CD.19．如图所示，在△ABC中，AB=AC，∠A=120°，AB的垂直平分线MN分别交BC、AB于点M、N，求证：CM=2BM．4BANMC20.如图，CE，CF分别平分∠ACB和它的外角∠ACG，EF//BC，EF交AC于D。试问DF=DE吗？请说出你的理由。ABCDEF21.如图，在Rt△ABC中，AB=AC，∠BAC=90°，D为BC的中点.（1）写出点D到ΔABC三个顶点A、B、C的距离的关系（不要求证明）（2）如果点M、N分别在线段AB、AC上移动，在移动中保持AN=BM，请判断△DMN的形状，并证明你的结论NMDBAC22.如图，△ABC中，∠BAC=900,D是△ABC内一点，若BD=AB=AC，∠ABD=300，求证：AD=DC523.如图，△ABC中,AB=AC,D是形外一点,且∠ABD=600,∠ACD=600,猜想BD,DC与AB之间有什么关系.并证明你的结论.24.如图,△ABC为等边三角形,延长BA到E,使AE=BD,连结CE、DE,求证:CE=DE.25.△ABC中，∠C=900,AC=BC，D为BC上一点，BE⊥AD于E点，且AD=2BE.求证：AD平分∠BAC26.已知：如图，在△ABC中，AB=AC,E在AC上，D在BA的延长线上，AD=AE，6连结DE。请问：DE⊥BC成立吗？27.如图，已知ABC△中，10ABAC厘米，8BC厘米，点D为AB的中点．（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，BPD△与CQP△是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使BPD△与CQP△全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿ABC△三边运动，求经过多长时间点P与点Q第一次在ABC△的哪条边上相遇？28.已知：A、B两点在直线l的同侧，试分别画出符合条件的点M．AQCDBP7（1）如图1，在l上求作一点M，使得｜AM－BM｜最小；作法：（2）如图2，在l上求作一点M，使得｜AM－BM｜最大；作法：（3）如图3，在l上求作一点M，使得AM＋BM最小．例1.如图，已知ΔABC中，AD是∠BAC的平分线，AD又是BC边上的中线。求证：ΔABC是等腰三角形。8例2.如图，ΔABC中，AB=AC，E是AB上一点，F是AC延长线上一点，连EF交BC于D，若EB=CF。求证：DE=DF。例3.△ABC中，∠BAC=60°，∠C=40°，AP平分∠BAC交BC于P，BQ平分∠ABC交AC于Q，求证：AB+BP=BQ+AQ。例4.如图，AD∥BC，点E在线段AB上，∠ADE=∠CDE，∠DCE=∠ECB。求证：CD=AD+BC。9轴对称综合参考答案例1.证明：延长AD到E，使DE=AD，连接BE。又因为AD是BC边上的中线，∴BD=DC又∠BDE=∠CDAΔBED≌ΔCAD，故EB=AC，∠E=∠2，∵AD是∠BAC的平分线∴∠1=∠2，∴∠1=∠E，∴AB=EB，从而AB=AC，即ΔABC是等腰三角形。例2.证明：过E作EG//AC交BC于G，则∠EGB=∠ACB，又AB=AC，∴∠B=∠ACB，∴∠B=∠EGB，∴∠EGD=∠DCF，∴EB=EG=CF，∵∠EDB=∠CDF，∴ΔDGE≌ΔDCF，∴DE=DF。例3.证明：过O作OD∥BC交AB于D，∴∠ADO=∠ABC=180°－60°－40°=80°，又∵∠AQO=∠C+∠QBC=80°，∴∠ADO=∠AQO，又∵∠DAO=∠QAO，OA=AO，∴△ADO≌△AQO，∴OD=OQ，AD=AQ，10又∵OD∥BP，∴∠PBO=∠DOB，又∵∠PBO=∠DBO，∴∠DBO=∠DOB，∴BD=OD，又∵∠BPA=∠C+∠PAC=70°，∠BOP=∠OBA+∠BAO=70°，∴∠BOP=∠BPO，∴BP=OB，∴AB+BP=AD+DB+BP=AQ+OQ+BO=AQ+BQ。例4.证明：在CD上截取CF=BC，如图乙∴△FCE≌△BCE（SAS），∴∠2=∠1。又∵AD∥BC，∴∠ADC+∠BCD=180°，∴∠DCE+∠CDE=90°，∴∠2+∠3=90°，∠1+∠4=90°，∴∠3=∠4。在△FDE与△ADE中，∴△FDE≌△ADE（ASA），∴DF=DA，∵CD=DF+CF，11∴CD=AD+BC。A档（巩固专练）1.B2.C3.B4.C5.C6.D7.D8.C9.CB档（提升精练）10.611.1,-112.1a13.55°，55°或70°，40°14.915.3cm，3cm，4cm或4cm，4cm，2cm16．（1）特征1：都是轴对称图形；特征2：都是中心对称图形；特征3：这些图形的面积都等于4个单位面积；等（2）满足条件的图形有很多，只要画正确一个，都可以得满分．17.731()44C档（跨越导练）18.在CD上截取DE=DB，连接AE，∵AD⊥BC，∴AE=AB.∴∠B=∠AEB.又∵∠AEB=∠C+∠CAE=2∠C，∴∠CAE=∠C.∴AE=EC.∴AB+BD=AE+BD=EC+ED=CD.∴AB+BD=CD.19.证法1：如答图所示，连接AM，∵∠BAC=120°，AB=AC，∴∠B=∠C=30°，∵MN是AB的垂直平分线，∴BM=AM，∴∠BAM=∠B=30°，∴∠MAC=90°，∴CM=2AM，∴CM=2BM．证法二：如答图所示，过A作AD∥MN交BC于点D．∵MN是AB的垂直平分线，∴N是AB的中点．∵AD∥MN，∴M是BD的中点，即BM=MD．∵AC=AB，∠BAC=120°，∴∠B=∠C=30°，∵∠BAD=∠BNM=90°，∴AD=BD=BM=MD，又∵∠CAD=∠BAC-∠BAD=120°-90°=30°，∴∠CAD=∠C，∴AD=DC，BM=MD=DC，∴CM=2BM．20.分别证明DE=DC，DF=DC，所以DE=DF1221.(1)DA=DB=DC(2)△DMN为等腰直角三角形证明：连结AD∵∠DBA=∠DAC=45°，BM=AN，BD=AD∴△DBM全等于△DAN∴DM=DN，∠BDM=∠ADN∵∠ADN+∠CDN=∠ADC=90°∴∠BDM+∠CDN=90°∴∠MDN=90°22.分析：见到300角，最好将它放到某个直角三角形中。证明：作AE⊥BD于E，DF⊥AC于F。在Rt△ABE中,∠ABD=300,得ABAE21，由BD=AB=AC，得∠BAD=∠BDA，ACAE21由∠ABD=300，得∠BAD=∠BDA=750，则∠DAC=900-750=150，又DF⊥AC，则∠FDA=900-750=150，即DA平分∠FDE，得AE=AF则ACAF21又DF⊥AC则AD=DC23.分析：见到600的角，应该想到将其放到某个等腰三角形中。由∠ABD=600，可构造等边三角形△ABE，或等边三角形△BDM由∠ACD=600，可构造等边三角形△ACN，或等边三角形△CDP解：经过测量，猜想BD+DC=AB，下面来证明这个结论。延长BD至E，使BE=AB，连接AE，CE。如图（4-2）由∠ABD=600，BE=AB，得到△ABE是等边三角形。即AB=BE=AE，∠AEB=600，已知∠ACD=600,得∠ACD=∠AEB,又AB=AC,则,AE=AC,则∠ACE=∠AEC,所以∠ACE-∠ACD=∠AEC-∠AEB,即∠DCE=∠DEC,则CD=DE所以BD+DC=BD+DE=BE=AB24.分析:如果CE=DE,那么CE和DE是关于CD的中垂线对称的两条线段,我们依照”补齐“图形的原则,延长BD到F,使DF=BC,补成一个轴对称图形即等边三角形EBF,只要证明△EBC≌△EFD就可以了.证明:延长BD到F,使DF=BC,连结EF.∵△ABC是等边三角形∴AB=BC,∠ABC=60°,∴BE=BA+AE=BC+BD=BD+DF,∴BE=BF∴△EBF为等腰三角形,又∵∠ABC=60°∴△EBF为等边三角形,∴∠ABC=∠EFB.在△EBC和△EFD中,BE=FE,∠EBC=∠EFD=60°,BC=DF,∴△EBC≌△EFD,∴CE=ED.25.要证明AD平分∠BAC,只要说明AD所在直线是轴对称图形的对称轴,