当前位置:首页 > 高等教育 > 大学课件 > 《因式分解专题训练》有答案
整式和因式分解1因式分解专题训练一、整式有关概念:1.单项式(单个字母或数)(次数,系数);2.多项式(次数,项数)3.同类项与合并同类项二、幂的运算性质:1.nmnmaaa2.mnnmaa3.nnnbaab4.nnnbaba5.nmnmaaa6.10a7.ppaa18.ppbaab三、整式的运算:加、减、乘、除(乘方、开方)1.m(a+b+c)=ma+mb+mc2.(a+b)(m+n)=am+an+bm+bn3.(a+b)(a-b)=22ba4.2222ababab5.cabcabcbacba22222226.3322babababa7.cabcabcbaaccbba222222222222四、因式分解:1.把一个多项式化成几个整式的积的形式.2.方法(一提二套三分组)(套公式包括十字相乘法)五、方法·规律·技巧:1.性质、公式的逆向使用;2.整体代入(配方、换元)3.非负数的运用(配方)六、实际运用1.下列变形中,正确的是()A.123422xxxB.112xxxxC.22yxyxyxD.xxxx112.若nmnmbba224a52与可以合并成一项,则nm的值是()A.2B.0C.-1D.13.若22ba,ab=2,则22ba的值为()A.6B.4C.23D.324.把多项式xxx1212323分解因式,结果正解的是()A.4432xxxB.243xxC.223xxxD.223xx5.已知0322xx,则xx422的值为()A.-6B.6C.-2或6D.-2或306.下列等式从左到右的的变形,属于因式分解的是()A.a(x-y)=ax-ayB.12122xxxxC.34312xxxxD.11x3xxxx整式和因式分解27.因式分解:21622xxx=.8.分解因式:(a-b)(a-4b)+ab=.9.分解因式:9332xxx=.10.分解因式:22mymx=.11.多项式4x2+1加上一个单项式后能成为一个完全平方式,请你写出符合条件的所有的单项式:.12.计算:20172016201642125.0=.13.已知nmnmaaa4323,16,64则.14.已知634x964322xxx,则.15.若222222,121yxyxyx=.16、将下列各式分解因式:(1)xaxx2842(2)xyxyyx2712322(3)baba22(4)321612xax17.将下列各式分解因式:(1)42161259yx(2)3394xyyx(3)221162xx(4)222516baba(5)2244yxyx(6)22363ayaxyax(7)172x4912x(8)9326322yxyx整式和因式分解3(9)222510babababa(10)1222222xxxx18.将下列各式分解因式:(1)232xx(2)1322xx(3)22144yxyx(4)32212mxmxm19.将下列各式分解因式:(1)abybax2249(2)212nnnxxx(3)xyyx41122(4)13322132222xxxx(5)15222222xxxx(6)(x+1)(x+2)(x+3)(x+4)-12020.将下列各式分解因式:(1)9622yxx(2)abba44422(3)2212baa(4)3223yxyyxx21.简便计算:(1)1323.16523.14823.1-(2)814.13125.06.18(3)2.48.1425.042.032(4)7582-2582(5)99992+19998+1(6)20162-2015×2017整式和因式分解4(7)2222201611411311211(8)42017201420132013201620142014201622222.已知137373212xxxx可分解因式为bxax3,其中a、b都是整数,求a+3b的值.23.已知2222912x4,010644yxyyxyx求的值.24.已知13,022232xxxx求的值.25.已知n为正整数,试说明nn332能被24整除.26.若5522,,1,1nmnmnnmm求的值.27.设222222211212,...,35,13nnaaan(n是大于0的自然数)。(1)探究an是否为8的倍数,并用文字语言表达你所获得的结论;(2)试找出naaa,...,,21,这一列数中从小到大排列的前4个完全平方数,并指出当n满足什么条件时,an是完全平方数(不必说明理由).整式和因式分解5因式分解专题训练答案CDBDBD7、(x-2)(x+4)(x-4)8、(a-2b)29、(x-3)(4x+3)10、m(x+y)(x-y)11、4x,-4x,4x412、413、1/414、715、4(负值舍去)16、(1)-2x(2x+4a-1)(2)-3xy(x-4y+9)(3)(a-b)(2a-2b-1)(4)2(x-1)2(1+3ax-3a)17、(1)2241534153yxyx(2)xy(2x+3y)(2x-3y)(3)3(x-2)(5x-2)(4)-(9a+b)(a+9b)(5)-(x-2y)2(6)3a(x+y)2(7)(71x-1)2(8)(2x+3y-3)2(9)4(3a-2b)2(10)(x-1)418、(1)(x-1)(x-2)(2)(2x+1)(x+1)(3)(x-2y)(4x+7y)(4)(x+1)[(m-1)x+(m+1)]19、(1)(a-b)(3x+2y)(3x-2y)(2)xn(1-x)2(3)(xy-1+x+y)(xy-1-x-y)(4)x(2x-3)(x-3)(2x+3)(5)(x+1)(x-3)(x2-2x+5)(6)(x-1)(x+6)(x2+5x+6)20、(1)(y+x-3)(y-x+3)(2)(a-2b+2)(a-2b-2)(3)(b+a+1)(b-a-1)(4)(x+y)2(x-y)21、(1)123(2)4(3)42(4)508000(5)108(6)1(7)141233222016)8(;40322017222xxxxxxxxx,则原式==设22、a=-7,b=-34;=-10923、(2x-1)2+(y+3)2=0,=10024、=325、=8×326、m5=m3×m2=m3(m+1)=m4+m3=(m2)2+m(m+1)=(m+1)2+m2+m=5m+3同理:n5=5n+3∴m5+n5=5(m+n)+6;又∵m2-n2=m-n∴m+n=1∴m5+n5=1127、(1)an=(2n+1+2n-1)(2n+1-2n+1)=8n(2)a1=8,a2=16,...,a8=64,...,a32=32×8,...,a128=128×8∴当n为2的奇次方时,是an完全平方数,即n=22k-1时(k为正整数)

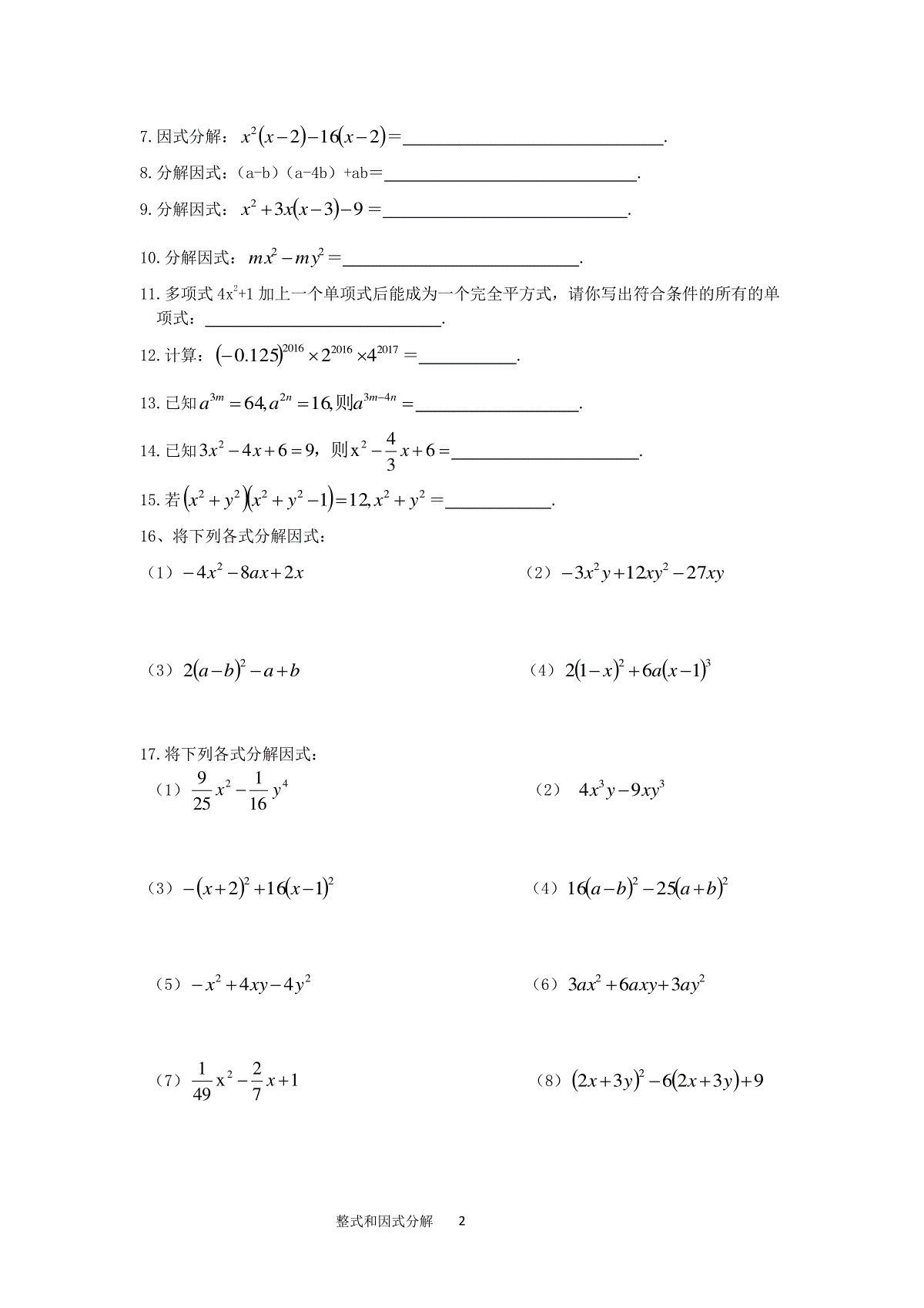
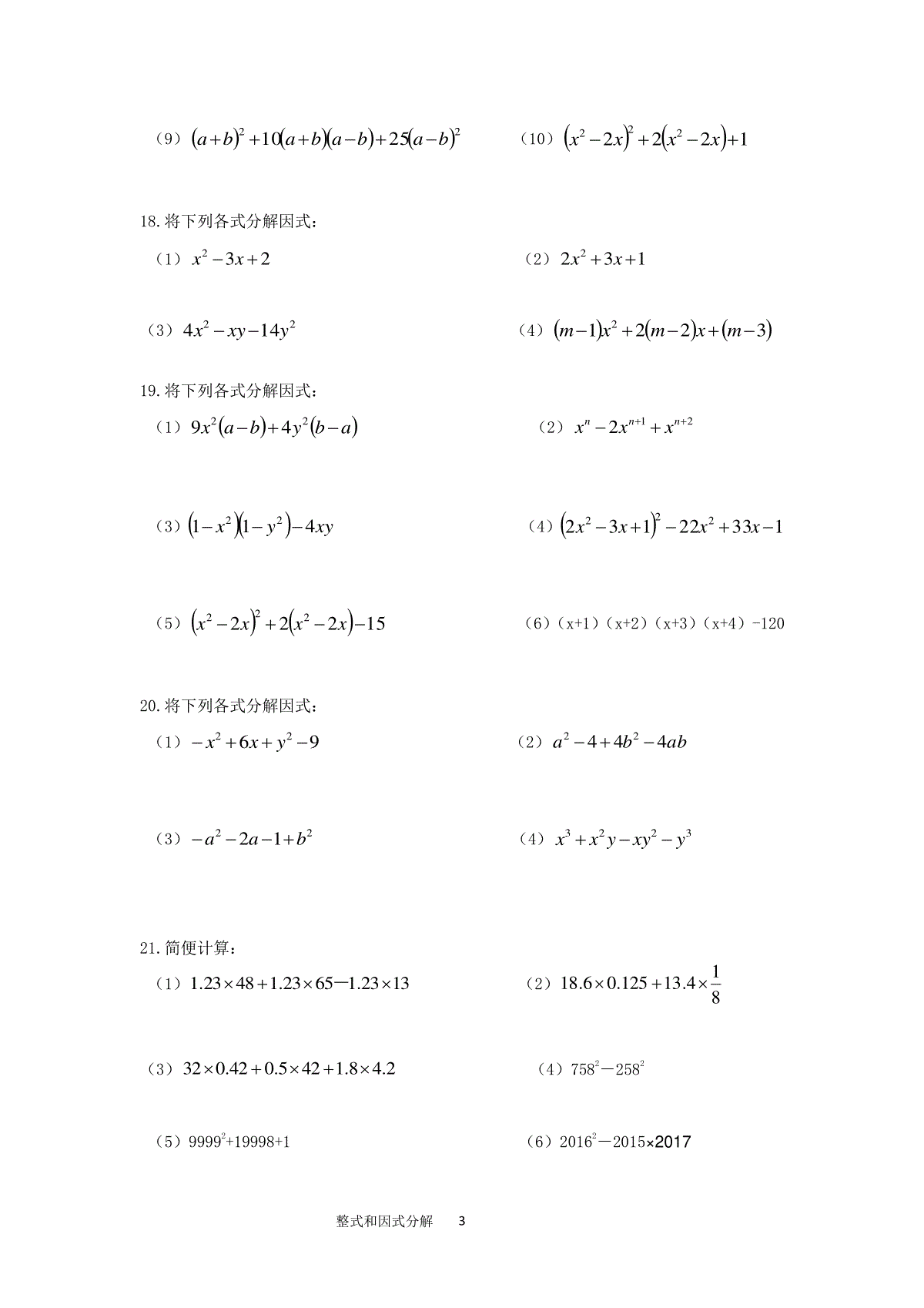


 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:《因式分解专题训练》有答案
链接地址:https://www.777doc.com/doc-6272274 .html