当前位置:首页 > 临时分类 > 拉普拉斯-傅里叶-z变换常用性质
1Laplace变换性质表名称时域s域定义1()2jstjtFsedsjf0,stFstedtf线性aftaft11221122aFsaFs尺度变换fatsFaaa01,时移ftttt00steFs0,0fatbatbab,0,bsaseFaaa01,复频移astfteaaFss0,时域微分ft1sFsf00,nftnmnnmmsFssf1100时域积分ntfxdx0nFss01,maxft1Fsfss1110nftnmnnmmFsfss11110时域卷积ftft12()FsFs1212,max,时域相乘ftft12cjcjFFsdj1212s域微分ntftnndFsds0,s域积分ftt()sFd0,2初值定理sfsFs0lim,s为真分式终值定理sfsFss0lim,0在sFs的收敛域内Z变换性质名称k域z域定义112kfkFzzdzj,kkFzfkzz线性1122afkafk1122aFzaFz移位双边变换fkm,mzFzz单边变换,0fkmm10,mmkkzFzfkmzz,0fkmm10,mmmkkzFzfkzzz域尺度变换kafk,zFazaak域卷积12fkfk121212max,max,FzFzzz域微分,0mkfkm,mdzFzzdzz域积分,0fkkmkm1,mmzFzdzk域反转fk111,Fzz部分和kifi,max,11zFzzz3初值定理因果序列00limzfFz10lim,mmkzkfmzFzfkzz终值定理11lim,limzkzfFzfkz收敛,z01Fourier变换性质名称时域ftFj频域定义12jftFjedjtjFjftedtFjFjeRjX线性1122afkafk1122aFjaFj奇偶性ft为实函数*,,,FjFjRRXXFjFjftftftft,0,0FjRXFjjXRft为虚函数*,,,FjFjRRXXFjFj反转ftFj对称性Fjt2f尺度变换,0fata1Fjaa时移特性0ftt0jteFj4,0fatba1bjaeFjaa频移特性0jtfte0Fj卷积定理时域12ftft12FjFj频域12ftft121*2FjFj时域微分nftnjFj时域积分1ft10fFjj频域微分njtftnFj频域积分10ftFjtjt1Fj相关定理12122112RftftdtRftftdt*1212FRFjFj*2112FRFjFj
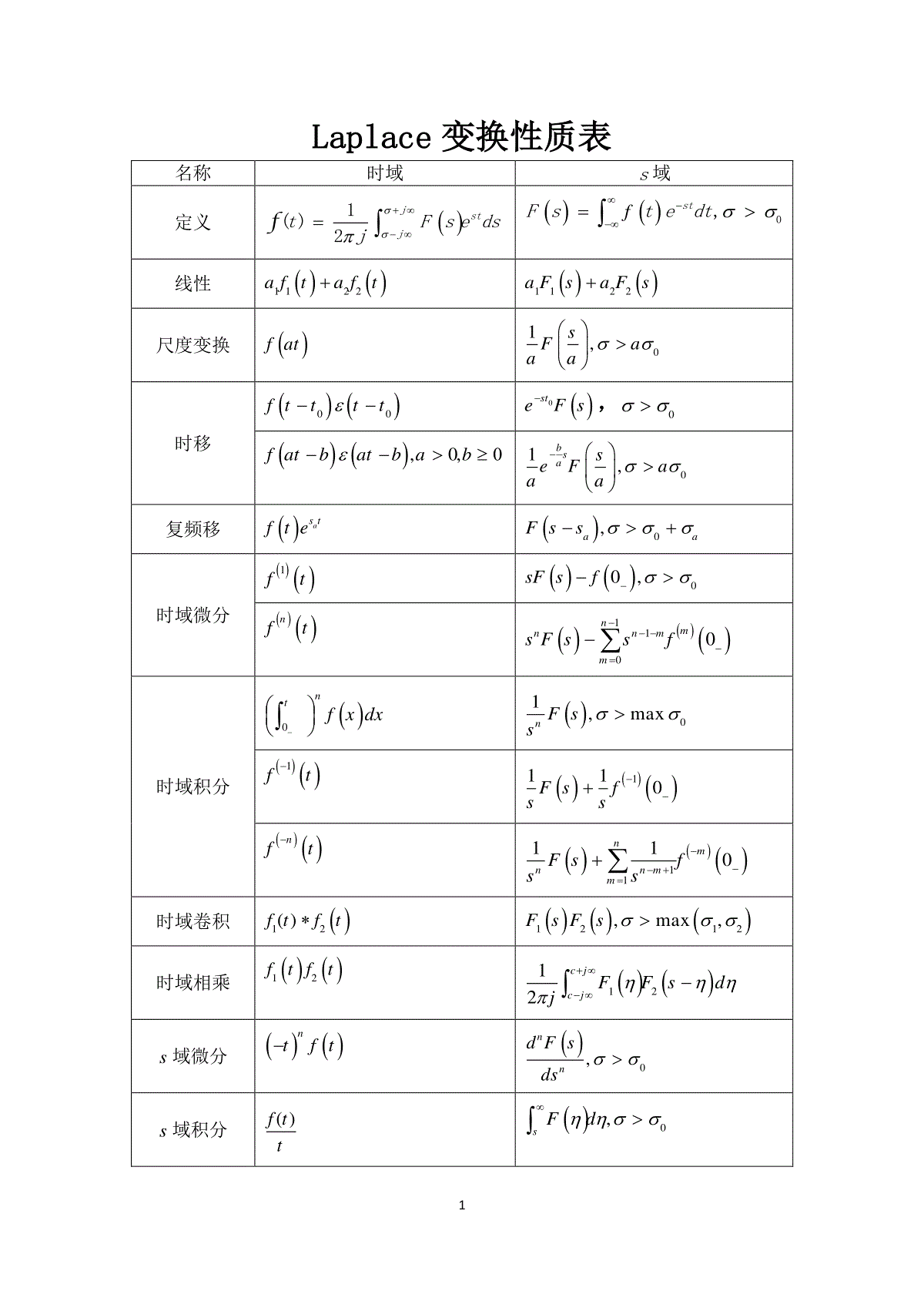



 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
 showricy
showricy
共133篇文档
格式: doc
大小: 348 KB
时间: 2020-09-14
本文标题:拉普拉斯-傅里叶-z变换常用性质
链接地址:https://www.777doc.com/doc-6925779 .html