韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档1专题十六三角恒等变换、三角函数的应用知识精讲一知识结构图内容考点关注点三角恒等变换、三角函数的应用利用两角和与差的正弦、余弦、正切公式求值、化简角的范围三角函数图象变换左右平移由图象求函数的解析式五个关键点三角恒等变换与三角函数图象性质的综合问题公式运用及三角函数的图象与性质二.学法指导1.解含非特殊角的三角函数式的求值问题的一般思路是:(1)把非特殊角转化为特殊角的和或差,正用公式直接求值.(2)在转化过程中,充分利用诱导公式,构造两角差的余弦公式的结构形式,然后逆用公式求值.2.给值求值问题的解题策略1已知某些角的三角函数值,求另外一些角的三角函数值时,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.2由于和、差角与单角是相对的,因此解题过程中可以根据需要灵活地进行拆角或凑角.常见角的变换有:①α=α-β+β;②α=α+β2+α-β2;③2α=α+β+α-β;④2β=α+β-α-β.韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档23.已知三角函数值求角的解题步骤1界定角的范围,根据条件确定所求角的范围.2求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.3结合三角函数值及角的范围求角.4.辅助角公式及其运用1公式形式:公式asinα+bcosα=a2+b2sinα+φ或asinα+bcosα=a2+b2cosα-φ将形如asinα+bcosαa,b不同时为零的三角函数式收缩为同一个角的一种三角函数式.2形式选择:化为正弦还是余弦,要看具体条件而定,一般要求变形后角α的系数为正,这样更有利于研究函数的性质.5.公式T(α±β)的结构特征和符号规律:(1)结构特征:公式T(α±β)的右侧为分式形式,其中分子为tanα与tanβ的和或差,分母为1与tanαtanβ的差或和.(2)符号规律:分子同,分母反.6.利用公式T(α+β)求角的步骤:(1)计算待求角的正切值.(2)缩小待求角的范围,特别注意隐含的信息.(3)根据角的范围及三角函数值确定角.7.公式Tα±β的逆用一方面要熟记公式的结构,另一方面要注意常值代换.如tanπ4=1,tanπ6=33,tanπ3=3等.要特别注意tanπ4+α=1+tanα1-tanα,tanπ4-α=1-tanα1+tanα.8.证明三角恒等式的原则与步骤1观察恒等式两端的结构形式,处理原则是从复杂到简单,高次降低,复角化单角,如果两端韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档3都比较复杂,就将两端都化简,即采用“两头凑”的思想.2证明恒等式的一般步骤:①先观察,找出角、函数名称、式子结构等方面的差异;②本着“复角化单角”“异名化同名”“变换式子结构”“变量集中”等原则,设法消除差异,达到证明的目的.9.化简问题中的“三变”(1)变角:三角变换时通常先寻找式子中各角之间的联系,通过拆、凑等手段消除角之间的差异,合理选择联系它们的公式.(2)变名:观察三角函数种类的差异,尽量统一函数的名称,如统一为弦或统一为切.(3)变式:观察式子的结构形式的差异,选择适当的变形途径,如升幂、降幂、配方、开方等.10.三角恒等变换与三角函数图象性质的综合问题的解题策略:运用三角函数的和、差、倍角公式将函数关系式化成y=asinωx+bcosωx+k的形式,借助辅助角公式化为y=Asinωx+φ+k或y=Acosωx+φ+k的形式,将ωx+φ看作一个整体研究函数的性质.11.应用三角函数解实际问题的方法及注意事项1方法:解答此类问题,关键是合理引入辅助角,确定各量之间的关系,将实际问题转化为三角函数问题,再利用三角函数的有关知识求解.2注意:在求解过程中,要注意三点:①充分借助平面几何性质,寻找数量关系.②注意实际问题中变量的范围.③重视三角函数有界性的影响.12.由y=sinx的图象,通过变换可得到函数y=Asin(ωx+φ)(A>0,ω>0)的图象,其变化途径有两条:(1)y=sinx――――→相位变换y=sin(x+φ)――――→周期变换y=sin(ωx+φ)――――→振幅变换y=Asin(ωx+φ).(2)y=sinx――――→周期变换y=sinωx――――→相位变换y=sinωx+φω=sin(ωx+φ)――――→振幅变换y=Asin(ωx+φ).韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档413.确定函数y=Asinωx+φ的解析式的关键是φ的确定,常用方法有:1代入法:把图象上的一个已知点代入此时A,ω已知或代入图象与x轴的交点求解此时要注意交点在上升区间上还是在下降区间上.2五点法:确定φ值时,往往以寻找“五点法”中的第一个零点-φω,0作为突破口.“五点”的ωx+φ的值具体如下:,“第一点”即图象上升时与x轴的交点为ωx+φ=0;,“第二点”即图象的“峰点”为ωx+φ=π2;,“第三点”即图象下降时与x轴的交点为ωx+φ=π;,“第四点”即图象的“谷点”为ωx+φ=3π2;,“第五点”为ωx+φ=2π.14.正弦余弦型函数奇偶性的判断方法正弦型函数y=Asin(ωx+φ)和余弦型函数y=Acos(ωx+φ)不一定具备奇偶性.对于函数y=Asin(ωx+φ),当φ=kπ(k∈Z)时为奇函数,当φ=kπ±π2(k∈Z)时为偶函数;对于函数y=Acos(ωx+φ),当φ=kπ(k∈Z)时为偶函数,当φ=kπ±π2(k∈Z)时为奇函数.15.与正弦、余弦函数有关的单调区间的求解技巧(1)结合正弦、余弦函数的图象,熟记它们的单调区间.(2)确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采用“换元”法整体代换,将ωx+φ看作一个整体,可令“z=ωx+φ”,即通过求y=Asinz的单调区间而求出函数的单调区间.若ω<0,则可利用诱导公式先将x的系数转变为正数,再求单调区间.16.解三角函数应用问题的基本步骤韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档5三.知识点贯通知识点1给角求值问题公式:cos(α-β)=cos_αcos_β+sin_αsin_βcos(α+β)=cos_αcos_β-sin_αsin_βsin(α+β)=sin_αcos_β+cos_αsin_βsin(α-β)=sin_αcos_β-cos_αsin_βsin2α=2sin_αcos_αcos2α=cos2α-sin2αtan2α=2tanα1-tan2α例1.(1)cos13π12的值为()A.6+24B.6-24C.2-64D.-6+24](2)求值:cos75°cos15°-sin75°sin195°;韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档6(3)cos70°sin50°-cos200°sin40°的值为()A.-32B.-12C.12D.32(4)若θ是第二象限角且sinθ=513,则cos(θ+60°)=________.(5)求值:(tan10°-3)cos10°sin50°.(6)cosπ7cos3π7cos5π7的值为()A.14B.-14C.18D.-18(7)求下列各式的值:①cos415°-sin415°;②1-tan275°tan75°韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档7知识点二给值求值、求角问题公式:cos(α-β)=cos_αcos_β+sin_αsin_βcos(α+β)=cos_αcos_β-sin_αsin_βsin(α+β)=sin_αcos_β+cos_αsin_βsin(α-β)=sin_αcos_β-cos_αsin_β例题2:(1)已知sinα-sinβ=1-32,cosα-cosβ=12,则cos(α-β)=()A.-32B.-12C.12D.32(2)已知sinπ3+α=1213,α∈π6,2π3,求cosα的值.(3)已知cosα=55,sin(α-β)=1010,且α,β∈0,π2.求:①cos(2α-β)的值;②β的值.韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档8(4)已知锐角α,β满足cosα=255,sin(α-β)=-35,求sinβ的值.(5)已知cosα+π4=35,π2≤α<3π2,求cos2α+π4的值;知识点三辅助角公式的应用辅助角公式:asinx+bcosx=a2+b2sin(x+φ),其中tanφ=ba例题3.(1)sinπ12-3cosπ12=________.(2)已知f(x)=3sinx-cosx,求函数f(x)的周期,值域,单调递增区间.韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档9知识点四两角和与差的正切公式的运用两角和与差的正切公式tan(α+β)=tanα+tanβ1-tanαtanβtan(α-β)=tanα-tanβ1+tanαtanβ例题4.(1)已知α,β均为锐角,tanα=12,tanβ=13,则α+β=________.(2)1+tan15°1-tan15°=________.(3)1-3tan75°3+tan75°=________.知识点五恒等变换与三角函数图象性质的综合例5.已知函数f(x)=3cos2x-π3-2sinxcosx.韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档10(1)求f(x)的最小正周期.(2)求证:当x∈-π4,π4时,f(x)≥-12.知识点六三角函数图象之间的变换1.φ对y=sin(x+φ),x∈R的图象的影响2.ω(ω>0)对y=sin(ωx+φ)的图象的影响3.A(A>0)对y=Asin(ωx+φ)的图象的影响韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档11例6.(1)将函数y=2cos2x+π3的图象向左平移π3个单位长度,再向下平移3个单位长度,则所得图象的解析式为________.(2)将y=sinx的图象怎样变换可得到函数y=2sin(2x+π4)+1的图象?知识点七已知函数图象求解析式例7.已知函数f(x)=Acos(ωx+φ)+BA>0,ω>0,|φ|<π2的部分图象如图所示,则函数f(x)的解析式为()A.y=2cosx2-π4+4B.y=2cosx2+π4+4C.y=4cosx2-π4+2D.y=4cosx2+π4+2知识点八三角函数图象与性质的综合应用例8(1)已知函数f(x)=sinωx+π3(ω>0),若fπ6=fπ3,且f(x)在区间π6,π3上有最小值,无最大值,则ω=()A.23B.143C.263D.383韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档12(2)已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ<π)是R上的偶函数,其图象关于点M3π4,0对称,且在区间0,π2上是单调函数,求φ和ω的值.知识点九三角函数模型的实际应用例9.已知某海滨浴场的海浪高度y(米)是时间t(时)的函数,其中0≤t≤24,记y=f(t),下表是某日各时的浪高数据:t03691215182124y1.51.00.51.01.510.50.991.5经长期观测,y=f(t)的图象可近似地看成是函数y=Acosωt+b的图象.(1)根据以上数据,求其最小正周期,振幅及函数解析式;(2)根据规定,当海浪高度大于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的8:00到20:00之间,有多少时间可供冲浪者进行活动?韩哥智慧之窗-精品文档韩哥智慧之窗-精品文档13五易错点分析易错一给值求角例题10.已知α,β均为锐角,sinα=55,cosβ=1010,求α-β.易错二三角函数图像平移例题11.要得到y=cos2x-π4的图象,只要将y=sin2x的图象()A.向左平移π8个单位B.向右平移π8个单位C.向左平移π4个单位D.向右平移π4个单位




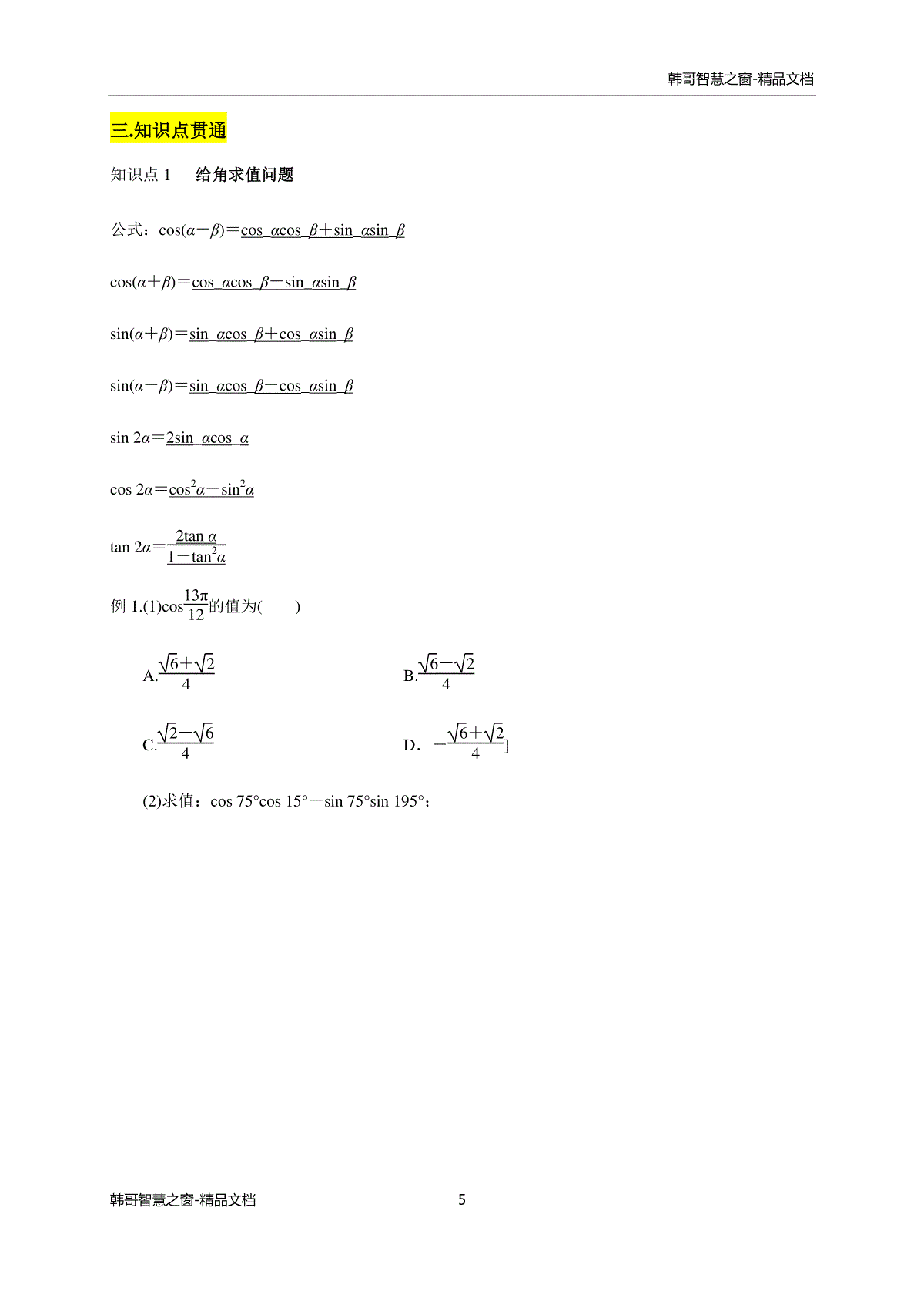
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:-三角恒等变换、三角函数的应用(知识精讲)-2019-2020高一数学(人教A版必修第一册)(原卷版
链接地址:https://www.777doc.com/doc-7438846 .html