当前位置:首页 > 幼儿/小学教育 > 小学教育 > 整式的运算专项练习题
【认识单项式与多项式】1、单项式32ab的次数是;系数是。2、多项式3x2y2-6xyz+3xy2-7是次多项式。3、已知–8xmy2m+1+12x4y2+4是一个七次多项式,则m=4、若46xy与133mnxy是同类项,则mn=_________5、12ayx与313yxb的和仍是一个单项式,a=.b=.和是.6、如果一个多项式的各项次数都相同,则称该多项式为齐次多项式。例如:32322yxyzxyx是3次齐次多项式。若23223zxyyxm是齐次多项式,则m等于_______________。7、在代数式22221,5,,3,1,35xxxxxx中是整式的有()个A、3B、4C、5D68、在下列代数式:1,212,3,1,21,2122xxbabbaab中,多项式有()A.2个B.3个C.4个D.5个9、在代数式xx3252,yx22,x1,5,a,0中,单项式的个数是()A、1B、2C、3D、410、若关于x的多项式12232xkxx不含x的一次项,则k的值为()A、41B、41C、4D、4【法则计算】1、23x,302)21(=。2、2xy2·(-3xy)2=1、02005,2)21(.100×103×104=;-2a3b4÷12a3b2=;3、计算:)()()(32xxx••=;4、计算:ababab21)232(2=。【法则的灵活运用】1、若ax=2,ay=8,则ax-y=。2、若ma=2,na=3,则nma的值是。3、若10m=5,10n=3,则102m-3n的值是4、已知2,322yxyxyx,则2232yxyx__________。5、如果2005m与22006n互为相反数,那么2007mn=。6、2005200640.25.2002200352.0;7、24212121的结果为.8、若51xx,则221xx。9、已知3,522baba,则_________ab。10、若16,9xyyx,求22yx。11、已知x-y=3,xy=1,则22yx()12、(3m+6)0=1,则m的取值范围是13、已知m+n=2,mn=-2,则(1-m)(1-n)的值为()14、当x=3时,代数式px3+qx+3的值是2005,则当x=-3时,代数式px3+qx+3的值为()A、2002B、1999C、-2001D、-199915、已知42xyy4x2x22,求yx________.16、若a2+b2-2a+2b+2=0,则a2004+b2005=________.17、要使4x2+25+mx成为一个完全平方式,则m的值是()A、10B、±10C、20D、±2018、若)3)((xmx中不含x得一次项,则m的值为________;19、2332xnxx的积中不含x的二次项,则n的值________20、)()()(23nmmnnm,【认识平方差公式与完全平方公式】1、下列计算中不能用平方差公式计算的是()A、(2x-y)(-2x+y)B、(m3-n3)(m3+n3)C、(-x-y)(x-y)D、(a2-b2)(b2+a2)2、下列各题中,能用平方差公式的是()A.(a-2b)(a+2b)B.(a-2b)(-a+2b)C.(-a-2b)(-a-2b)D.(-a-2b)(a+2b)3.22425xkxyy是一个完全平方式,则k=.4、已知x2-ax+49=(x+7)2对于任意x都成立,则a的值为()A、a=-7B、a=-14C、a=±7D、a=±145、若对于任意x值,等式(2x-5)2=4x2+mx+25恒成立。则m=[]A、20B、10C、-20D、-106、计算(-x-y)2等于()A.x2+2xy+y2B.-x2-2xy-y2C.x2-2xy+y2D.-x2+2xy-y27.下列式子加上a2-3ab+b2可以得到(a+b)2的是A.abB.3abC.5abD.7ab8、使nxxmx6)(22成立的常数m、n分别是()。(A)m=6、n=36(B)m=9、n=3(C)m=23、n=49(D)m=3、n=99、若3<a<5,,则︱5-a︱+︱3-a︱=;10、请你观察图形,依据图形面积之间的关系,不需要添加辅助线,便可得到一个你非常熟悉的公式,这个公式是()A、22))((yxyxyxB、2222)(yxyxyxC、2222)(yxyxyxD、222)(yxyxyx11、长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图(1),然后拼成一个梯形,如图(2),根据这两个图形的面积关系,表明下列式子成立的是()A、a2-b2=(a+b)(a-b).B、(a+b)2=a2+2ab+b2.C、(a-b)2=a2-2ab+b2.D、a2-b2=(a-b)2.12、李老师做了个长方形教具,一边长为ba2,另一边为ba,则该长方形周长为()A、ba6B、a6C、a3D、ba10【平方差公式的灵活运用】1、)12)(12(12128422、)15)(15(15158423、)100411()411)(311)(211(2222【公式灵活运用】1.已知2m=5,2n=7,求24m+2n的值。2、已知x6b-·x21b+=x11,且y1a-·yb4-=y5,求a+b的值.3.已知am=2,an=7,求a3m+2n–a2n-3m的值。【用简便方法计算下列各题】1、200522、1999×20013、12345679012345678812345678924、3200019992)21()211()32(20042006200520045、20072-2006×20086.)4)(4(22aaaa7.2)12(yx8、)12)(12(yxyx9、2)())((yxyxyx10、1212baba11、0.1252004×82005【计算题集锦组一】1、22123)()(xxxxnn2、aaaa7232253、(—2006)0×2÷21+(—31)—2÷2—34、033)3()21()2(5、)2)(2(nmnm6、)2()1264(3223xyxyyxyx7、先化简,再计算:)()]2(2)2)(2[(22mnnmmnmn,其中10m,251n。8、16×2-4+(-13)0÷(-13)-29、)61()31(yxyx10、)21()23(3223ababbaba11、先化简,再求值)2(5))(()2(22xyyxyxyx,其中21,2yx12、1212baba13、(-a)2(a2)214、-[-(-x2)+2y2]-2(-x2+3y2)15、2009200953213516、(-1)2006+(-12)-2-(3.14-π)017、nmnm1118、(16x2y3z-4x3y2z)÷(8x2y2)19、2221(3)(32)2aabaabb20、yxyx22221、已知2m=5,2n=7,求24m+2n的值。【计算题集锦组二】1、(3)(3)mnmn2、3223332aaaa3、)1)(32(xx4、(0.125)2008.(-8)20095、x(x-3)-(x+2)(x-1)6、)(2)2(baba7、)4)(4(xyxy8、)2()(baba9、7(p3+p2-P-1)-2(p3+p)10、已知x6b-·x21b+=x11,且y1a-·yb4-=y5,求a+b的值.【计算题集锦组三1、(27a3-15a2+6a)(3a)2、(2x+y+1)(2x+y-1)3、(2x+3)(2x-3)-(2x-1)24.3232(1262)(2)abababab5.2(2)4()(2)xyxyxy6、104×100×10-27、5232322baabba8、1212122xxx9、200720052006210、已知2m=5,2n=7,求24m+2n的值。11、22232)2(21cbabca12、1122xxx13、)(2)2(baba14、xxx32)(-15、ababab21)232(216、022009)14.3()21()1(17、22()()xyxy28、3222)()(aaa29、)100411()411)(311)(211(222220、(-3)-2-(3.14-π)0+(-12)321、22232babaab22、7(p3+p2-P-1)-2(p3+p)23、(2x2y)2·(-7xy2)÷(14x4y3)24、(27a3-15a2+6a)(3a)25、(2x-y+1)(2x+y-1)26、)2()(baba27、7(p3+p2-P-1)-2(p3+p)28、(2x+y+1)(2x+y-1)29、2)3()32)(32(bababa30、21(k3-2k2+4k)-41(2k3-4k2—28k)31、045)3()21(232、21mmaa33、)()()(32xxx34、-3x(2x+5)-(5x+1)(x-2)35、(x-5)2-(x+5)(x-5)36、(2x+3)(2x-3)-(2x-1)237、(-2x-3)(2x-3)-(2x-1)238、)86)(93(xx39、(2x2)3-6x3(x3+2x2+x)40、)1)(1()2(2xxx43、2031200323244、514yy45、(0.1-2x)(0.1+2x)46、)416131(12222yxyxyx47、2)3()32)(32(bababa48、(x+1)(x+3)-(x-2)249、(a+b+3)(a+b-3)51、045)3()21(252、3222)()(aaa;53、22232)2(21cbabca54、)(5)21(22222abbaababa55、(2x2)3-6x3(x3+2x2+x)56、22()()xyxy57、1122xxx58、))()((22yxyxyx59、3240)21()21()21()2(60、[(b3)2·(-b4)3]÷(b6)261、(-1)2007+(-12)-2-(3.14-π)0.62、(—2003)0×2÷21+(—31)—2÷2—363、045)3()21(264、3232(1262)(2)abababab65、10)71()71(66、20082--2007×200967、[(x+1)(x+2)-2]÷x68(a-b-3)(a+b-3)69、化简求值:)(42)2)(2(22xyyxxyxy,其中10x251y;70、23)2)(2()3(2aaaa,其中71、当a=-3时,求多项式(7a2-4a)-(5a2-a-1)+(2-a2+4a)的值。72、先化简,再求值)2(5))(()2(22xyyxyxyx,其中21,2yx73、化简求值))(()2(2yxyxyx,其中21,2yx74、先化简,再求值)2(8)4()2(2xxxyyyx



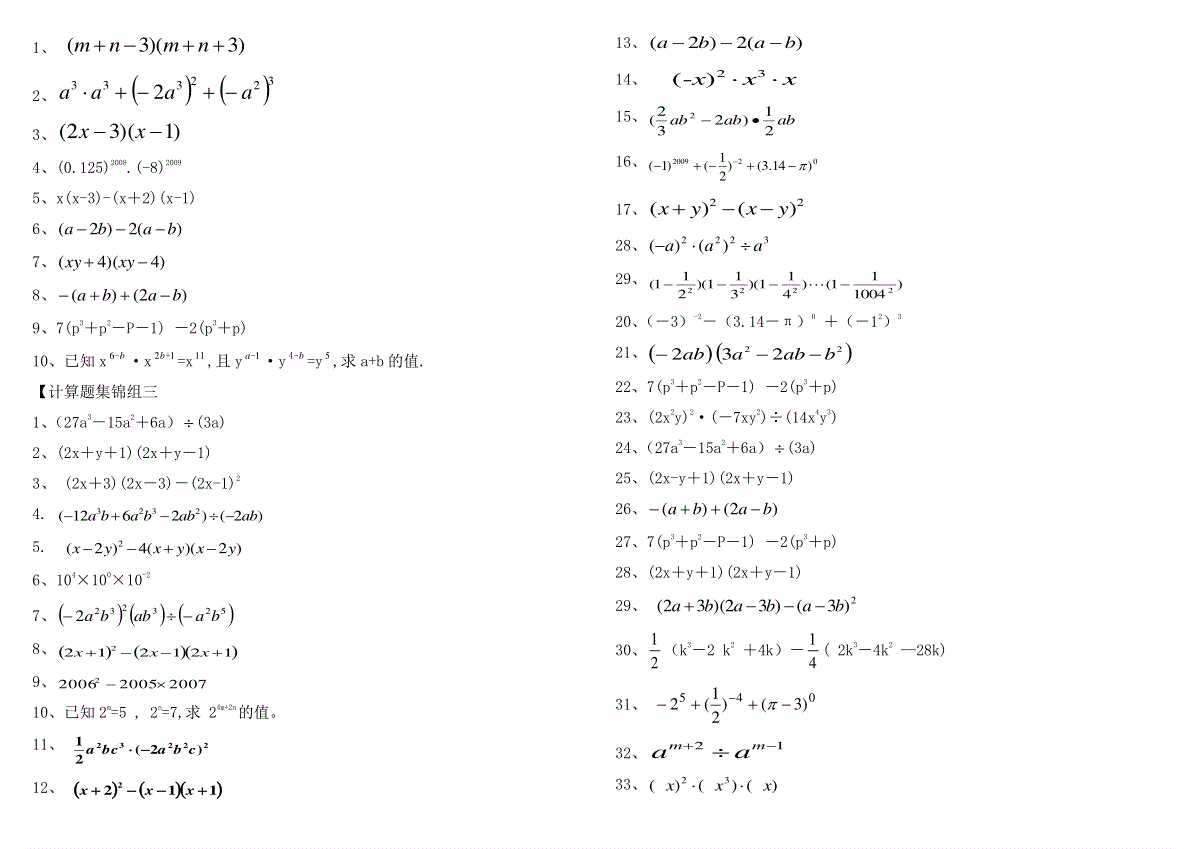
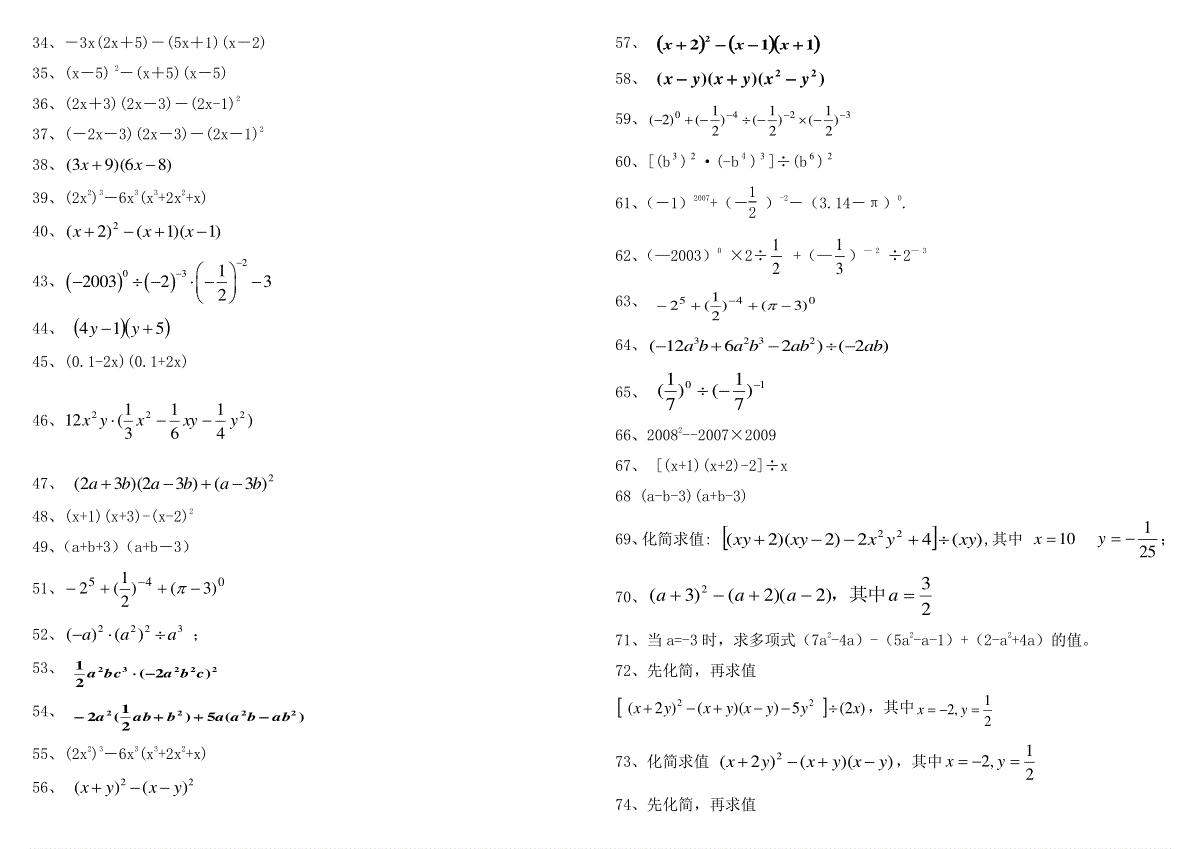
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:整式的运算专项练习题
链接地址:https://www.777doc.com/doc-7481176 .html