四川省泸州市泸县第二中学2019-2020学年高二数学上学期期中试题 文

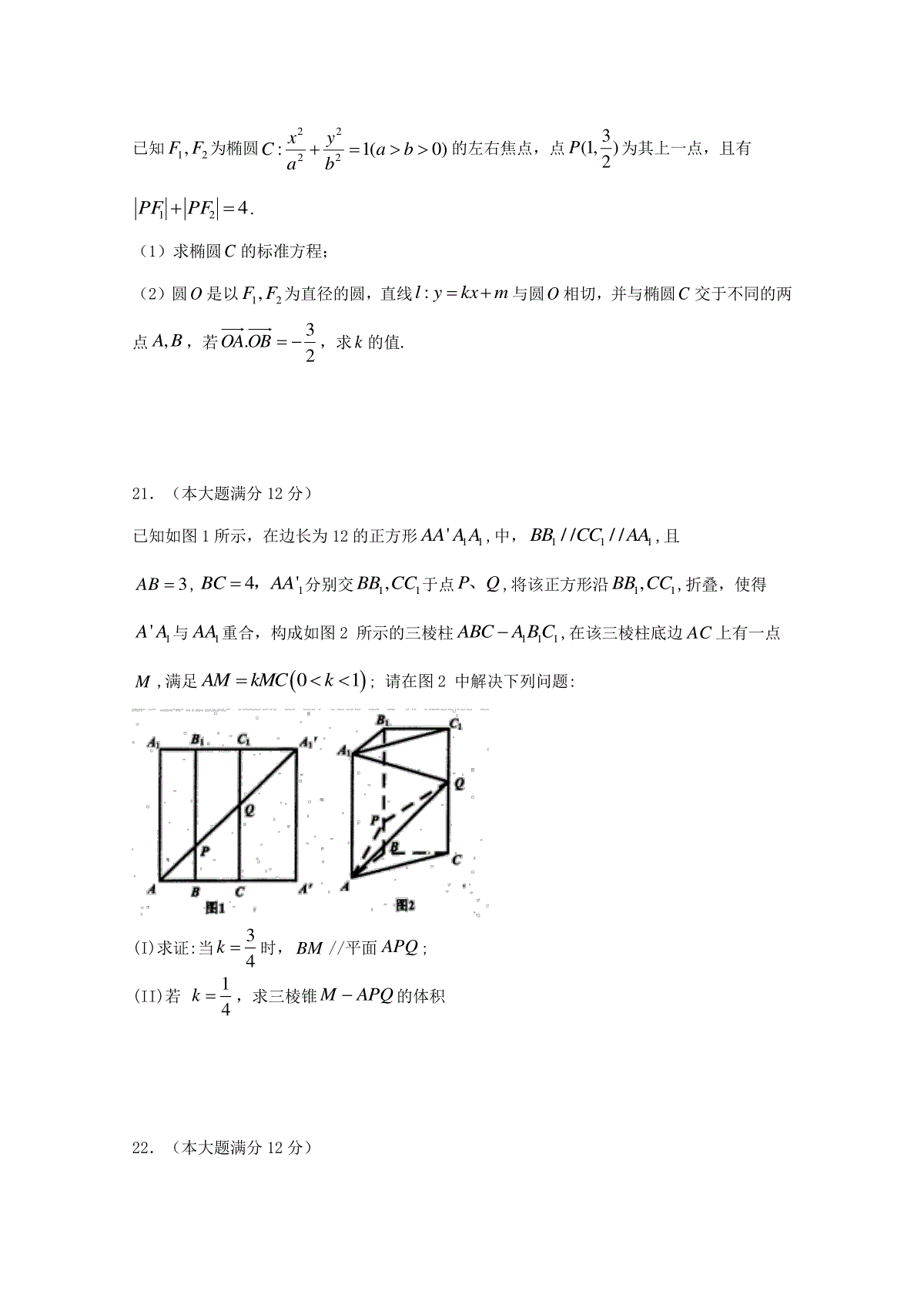
四川省泸州市泸县第二中学2019-2020学年高二数学上学期期中试题文第I卷(选择题共60分）一、选择题(本大题共12小题，每小题5分，共60分.在每个小题所给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在答题卡的指定位置.）1．在直角坐标系中，直线330xy的倾斜角是A．6B．3C．56D．232．已知,ab为非零实数，且ab，则下列不等式成立的是A.22abB.11abC.||||abD.22ab3．椭圆的离心率为A．23B．43C．22D．324．直线3x+4y-3=0与圆22(2)(3)1xy的位置关系是：A．相离;B．相交;C．相切;D．无法判定.5．设l为直线，,是两个不同的平面，下列命题中正确的是A．若//l，//l，则//B．若l，l，则//C．若l，//l，则//D．若，//l，则l6．已知直线L1：ax+3y﹣3＝0，与直线L2：4x+6y﹣1＝0平行，则a的值是A．8B．4C．2D．17．已知变量x，y满足约束条件0,{0,1,xyxy则223zxy的最小值为A.10B.22C.8D.108．已知圆221:40Cxy与圆222:44120Cxyxy相交于,AB两点，则两圆的公共弦ABA．22B．32C．2D．29．在圆22xy2x6y0内，过点E0,1的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为A．52B．102C．152D．20210．点P是直线20xy上的动点，点Q是圆221xy上的动点，则线段PQ长的最小值为A.21B.1C.21D.211．平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为2，则此球的体积为A．6πB．43πC．46πD．63π12．已知1F、2F分别是椭圆2222:1(0)xyCabab的左、右焦点，P是以12FF为直径的圆与椭圆C的一个交点，且12212PFFPFF，则椭圆C的离心率为A.31B.23C.312D.232第Ⅱ卷（非选择题共90分）二、填空题(本大题共4小题，每小题5分，满分20分）13．直线3x+2y+5＝0在x轴上的截距为_____．14．设x，y都是正数，且1213xy，则xy的最小值______________.15．已知双曲线222210,0xyabab的焦距为25，且双曲线的实轴长是虚轴长的2倍，则双曲线的方程为___________.16.直线33yxm与圆221xy在第一象限内有两个不同的交点，则实数m的取值范围是．三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤17．（本大题满分10分）已知ABC的三个顶点坐标分别为)3,3(),1,1(),4,2(CBA.（1）求边BC的垂直平分线的方程；（2）求ABC的面积.18．（本大题满分12分）设椭圆C：22221(0)xyabab过点0,3，离心率为12．（1）求椭圆C的方程；（2）设斜率为1的直线l过椭圆C的左焦点且与椭圆C相交于A，B两点，求AB的中点M的坐标．19．（本大题满分12分）已知圆22:2410Cxyxy，O为坐标原点，动点P在圆外，过点P作圆C的切线，设切点为M.（1）若点P运动到13，处，求此时切线l的方程；（2）求满足PMPO的点P的轨迹方程.20．（本大题满分12分）已知21,FF为椭圆)0(1:2222babyaxC的左右焦点，点)23,1(P为其上一点，且有421PFPF.（1）求椭圆C的标准方程；（2）圆O是以21,FF为直径的圆，直线mkxyl:与圆O相切，并与椭圆C交于不同的两点BA,，若23.OBOA，求k的值.21．（本大题满分12分）已知如图1所示，在边长为12的正方形11'AAAA,中，111////BBCCAA,且3AB,14'BCAA，分别交11,BBCC于点PQ、,将该正方形沿11,BBCC,折叠，使得1'AA与1AA重合，构成如图2所示的三棱柱111ABCABC,在该三棱柱底边AC上有一点M,满足01AMkMCk;请在图2中解决下列问题:(I)求证:当34k时，BM//平面APQ;(II)若14k，求三棱锥MAPQ的体积22．（本大题满分12分）已知12,FF分别是椭圆2222:1(0)xyEabab的左、右焦点，离心率为12，,MN分别是椭圆的上、下顶点，222MFNF.（1）求椭圆E的方程；（2）过(0,2)M作直线与E交于,AB两点，求三角形AOB面积的最大值（O是坐标原点）.2019-2020学年度秋四川省泸县第二中学高二期中考试文科数学试题参考答案1．C2．D3．A4．A5．B6．C7．D8．A9．B10．A11．B12．A13．5314．96215．2214xy16．2313m17．:（1）线段的中点的坐标为,又直线的斜率为,∴边的垂直平分线的斜率为,故边的垂直平分线的方程为,即.（2）,直线的方程是,即,点到直线的距离,的面积.18．（1）由椭圆C：22221(0)xyabab可知其焦点在x轴上，因为椭圆过点(0,3)，所以3b，因为其离心率22112cbeaa，解得24a，所以椭圆的标准方程为22143xy；（2）由题意可知：直线方程为1yx，由221431xyyx，整理得27880xx，显然，设1122(,),(,)AxyBxy，00(,)Mxy，由韦达定理可得1287xx，12128611277yyxx，所以AB中点M的坐标是43(,)77.19．解:把圆C的方程化为标准方程为（x＋1）2＋（y－2）2＝4，∴圆心为C（－1,2），半径r＝2.（1）当l的斜率不存在时，此时l的方程为x＝1，C到l的距离d＝2＝r，满足条件．当l的斜率存在时，设斜率为k，得l的方程为y－3＝k（x－1），即kx－y＋3－k＝0，则2|23|1kkk＝2，解得k＝34.∴l的方程为y－3＝34（x－1），即3x＋4y－15＝0.综上，满足条件的切线l的方程为1x或34150xy.（2）设P（x，y），则|PM|2＝|PC|2－|MC|2＝（x＋1）2＋（y－2）2－4，|PO|2＝x2＋y2，∵|PM|＝|PO|.∴（x＋1）2＋（y－2）2－4＝x2＋y2，整理，得2x－4y＋1＝0，∴点P的轨迹方程为2410xy.20：（1）由题意，椭圆的长轴长，得，因为点在椭圆上，∴，所以椭圆的标准方程为.（2）当直线与圆相切，得，即,设，由消去，整理得，由题意可知圆在椭圆内，所以直线必与椭圆相交，所以，，所以，因为，所以，又因为，所以，解得.21.(I)解:在图(2)中，过M作//MNCQ交AQ于N，连接PN，所以//MNPB,∴MNPB共面且平面MNPB交平面APQ于PN,∵3347MNAMkCQAC，又7,3,3CQMNMNPBAB,∴四边形MNPB为平行四边形，∴//BMPN,PN平面APQ,BM平面APQ,∴BM//平面APQ;(II)解:因为=3,=4ABBC,所以=5AC,从而222ACABBC,即ABBC.因为14k.所以1AM.所以_1112143255MAPQPAMQVVAMCQ22：（1）由题知，2,0Fc，0,Mb，0,Nb，∴22222MFNFcb，∴2222ab，①∵12cea，∴12ca，∴222234baca，②①②联立解得24a，23b，∴椭圆E的方程为22143xy．（2）设11,Axy，22,Bxy，显然直线AB斜率存在，设其方程为2ykx，代入2234120xy，整理得22341640kxkx，则221644340kk，即214k，1221634kxxk，122434xxk，22121214ABkxxxx2222164143434kkkk22224814143kkk，所以O到l的距离221dk，所以三角形AOB面积2222248141122143kkSkkk222341443kk，设2410tk，所以2333444316164828tStttttt，当且仅当16tt，即4t，即2414k，即52k时取等号，所以AOB面积的最大值为3．