2018-2019学年四川省南充市九年级(上)期末数学模拟试卷一.选择题(共10小题,满分30分,每小题3分)1.一元二次方程x2+5=﹣4x的一次项的系数是()A.4B.﹣4C.1D.52.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.3.方程x2﹣2x﹣3=0经过配方法化为(x+a)2=b的形式,正确的是()A.(x﹣1)2=4B.(x+1)4C.(x﹣1)2=16D.(x+1)2=164.下列事件中,属于必然事件的是()A.三角形的外心到三边的距离相等B.某射击运动员射击一次,命中靶心C.任意画一个三角形,其内角和是180°D.抛一枚硬币,落地后正面朝上5.圆锥的母线长是3,底面半径是1,则这个圆锥侧面展开图圆心角的度数为()A.90°B.120°C.150°D.180°6.一元二次方程x2+kx﹣3=0的一个根是x=1,则k的值为()A.2B.﹣2C.3D.﹣37.下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是()A.B.C.D.8.对于二次函数y=2(x﹣1)2+2的图象,下列说法正确的是()A.开口向下B.对称轴是直线x=﹣1C.顶点坐标是(1,2)D.与x轴有两个交点.9.如图是武汉某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为()A.13mB.15mC.20mD.26m10.如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0,②2a﹣b=0,③a+b+c<0;④c﹣a=3,其中正确的有()个.A.1B.2C.3D.4二.填空题(共6小题,满分18分,每小题3分)11.已知x=2是一元二次方程x2+mx+6=0的一个根,则方程的另一个根是.12.小明掷一枚均匀的骰子,骰子的六个面上分别刻有1,2,3,4,5,6点,得到的点数为奇数的概率是.13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0.其中,正确结论的有.14.如图,在△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=2,则扇形BDE的面积为.15.如图,四边形ABCD内接于圆O,若∠BOD=130°,则∠DCE=°.16.如图,△ABC为等边三角形,AB=3,若点P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为.三.解答题(共9小题,满分72分)17.解方程:x2﹣4=﹣3x﹣6.18.经过校园某路口的行人,可能左转,也可能直行或右转.假设这三种可能性相同,现有小明和小亮两人经过该路口,请用列表法或画树状图法,求两人之中至少有一人直行的概率.19.已知关于x的一元二次方程x2+3x﹣m=0有实数根.(1)求m的取值范围(2)若两实数根分别为x1和x2,且x12+x22=11,求m的值.20.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,将△ABO向左平移6个单位长度得到△A1B1O1;将△A1B1O1绕点B1按逆时针方向旋转90°后,得到△A2B2O2,请画出△A1B1O1和△A2B2O2,并直接写出点O2的坐标.21.如图,在平面直角坐标系中,⊙D与坐标轴分别相交于A(﹣,0),B(,0),C(0,3)三点.(1)求⊙D的半径;(2)E为优弧AB一动点(不与A,B,C三点重合),EN⊥x轴于点N,M为半径DE的中点,连接MN,求证:∠DMN=3∠MNE;(3)在(2)的条件下,当∠DMN=45°时,求E点的坐标.22.甲、乙两个工程队原计划修建一条长100千米的公路,由于实际情况,进行了两次改道,每次改道以相同的百分率增加修路长度,使得实际修建长度为121千米,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.(1)求两次改道的平均增长率;(2)求甲、乙两个工程队每天各修路多少千米?(3)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过42.4万元,甲工程队至少修路多少天?23.二次函数y=x2+mx+n的图象经过点A(﹣1,a),B(3,a),且最低点的纵坐标为﹣4.(1)求m、n和a的值;(2)若直线y=kx+2经过点A,求k的值;(3)记(1)中的二次函数图象在点A,B之间的部分图象为G(包含A,B两点),若直线y=kx+2与G有公共点,请结合图象探索实数k的取值范围.(注意:请在答题卡的直角坐标系中画出解题时使用的函数草图)24.如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.(1)试判断∠AED与∠C的数量关系,并说明理由;(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为.25.在直角坐标系xOy中,已知点P是反比例函数y=(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.(1)如图1,当⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由;(2)如图2,当⊙P运动到与x轴相交,设交点为点B、C.当四边形ABCP是菱形时,求出点A、B、C的坐标(3)在(2)的条件下,求出经过A、B、C三点的抛物线的解析式.参考答案一.选择题(共10小题,满分30分,每小题3分)1.【解答】解:方程整理得:x2+4x+5=0,则一次项系数为4.故选:A.2.【解答】解:A、不是轴对称图形,是中心对称图形,故此选项错误;B、不是轴对称图形,是中心对称图形,故此选项错误;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,也是中心对称图形,故此选项正确.故选:D.3.【解答】解:x2﹣2x+1﹣1﹣3=0,(x﹣1)2=4,故选:A.4.【解答】解:A、三角形的外心到三角形的三个顶点的距离相等,三角形的内心到三边的距离相等,只有三角形是等边三角形时才符合,故本选项不符合题意;B、某射击运动员射击一次,命中靶心是随机事件,故本选项不符合题意;C、三角形的内角和是180°,是必然事件,故本选项符合题意;D、抛一枚硬币,落地后正面朝上,是随机事件,故本选项不符合题意;故选:C.5.【解答】解:圆锥侧面展开图的弧长是:2πcm,设圆心角的度数是x度.则=2π,解得:x=120.故选:B.6.【解答】解:把x=1代入x2+kx﹣3=0中,得1+k﹣3=0,解得k=2,故选:A.7.【解答】解:A、B、C中只能由旋转得到,不能由平移得到,只有D可经过平移,又可经过旋转得到.故选:D.8.【解答】解:二次函数y=2(x﹣1)2+2的图象开口向上,顶点坐标为(1,2),对称轴为直线x=1,抛物线与x轴没有公共点.故选:C.9.【解答】解:如图,桥拱所在圆心为E,作EF⊥AB,垂足为F,并延长交圆于点H.由垂径定理知,点F是AB的中点.由题意知,FH=10﹣2=8,则AE=EH,EF=EH﹣HF.由勾股定理知,AE2=AF2+EF2=AF2+(AE﹣HF)2,解得AE=13m.故选:A.10.【解答】解:抛物线与x轴有两个交点,∴△>0,∴b2﹣4ac>0,故①错误;由于对称轴为x=﹣1,∴x=﹣3与x=1关于x=﹣1对称,∵x=﹣3时,y<0,∴x=1时,y=a+b+c<0,故③正确;∵对称轴为x=﹣=﹣1,∴2a﹣b=0,故②正确;∵顶点为B(﹣1,3),∴y=a﹣b+c=3,∴y=a﹣2a+c=3,即c﹣a=3,故④正确;故选:C.二.填空题(共6小题,满分18分,每小题3分)11.【解答】解:设方程的另一根为a,∵x=2是一元二次方程x2+mx+6=0的一个根,∴2a=6,解得a=3,即方程的另一个根是x=3,故答案为:x=3.12.【解答】解:根据题意知,掷一次骰子6个可能结果,而奇数有3个,所以掷到上面为奇数的概率为.故答案为:.13.【解答】解:由二次函数的图象与x轴两个交点可知,b2﹣4ac>0,故①正确;由二次函数的图象可知,开口向上,则a>0,顶点在y轴右侧,则b<0(左同右异),图象与y轴交于负半轴,则c<0,故abc>0,故②正确;由图象可知:,则b=﹣2a,当x=﹣2时,y=4a﹣2b+c>0,则y=4a﹣2×(﹣2a)+c>0,即8a+c>0,故③正确;由图象可知:此函数的对称轴为x=1,当x=﹣1时和x=3时的函数相等并且都小于0,故x=3时,y=9a+3b+c<0,故④正确;故答案为:①②③④.14.【解答】解:∵∠A=60°,∠B=100°,∴∠C=20°,∵BD=DC=1,DE=DB,∴DE=DC=1,∴∠DEC=∠C=20°,∴∠BDE=40°,∴扇形BDE的面积==,故答案为:.15.【解答】解:∵∠BOD=130°,∴∠A=∠BOD=65°,∵∠A+∠BCD=180°,∠DCE+∠BCD=180°,∴∠DCE=∠A=65°.故答案为:65.16.【解答】解:∵△ABC是等边三角形,∴∠ABC=∠BAC=60°,AC=AB=2,∵∠PAB=∠ACP,∴∠PAC+∠ACP=60°,∴∠APC=120°,∴点P的运动轨迹是,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:此时PA=PC,OB⊥AC,则AD=CD=AC=,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,∴PD=AD•tan30°=AD=,BD=AD=,∴PB=BD﹣PD=﹣=.故答案为:.三.解答题(共9小题,满分72分)17.【解答】解:x2﹣4=﹣3x﹣6,x2+3x+2=0,(x+2)(x+1)=0,x+2=0,x+1=0,x1=﹣2,x2=﹣1.18.【解答】解:画树状图为:共有9种等可能的结果数,其中两人之中至少有一人直行的结果数为5,所以两人之中至少有一人直行的概率为.19.【解答】解:(1)∵关于x的一元二次方程x2+3x﹣m=0有实数根,∴△=b2﹣4ac=32+4m≥0,解得:m≥﹣;(2)∵x1+x2=﹣3、x1x2=﹣m,∴x12+x22=(x1+x2)2﹣2x1•x2=11,∴(﹣3)2+2m=11,解得:m=1.20.【解答】解:如图所示,△A1B1O1、△A2B2O2即为所求:其中点O2的坐标为(﹣3,﹣3).21.【解答】(1)解:由于OA=OB=,且OD⊥AB,根据垂径定理知圆心D必在y轴上;连接AD,设⊙D的半径为R,则AD=R,OD=3﹣R;Rt△ADO中,根据垂径定理得:AD2=AO2+OD2,即R2=3+(3﹣R)2,解得R=2;即⊙D的半径为2;(2)证明:过D作DH⊥EN于H,连接MH;易知四边形DHNO是矩形,则HN=OD=1;Rt△DHE中,MH是斜边DE的中线,∴DM=ME=MH=DE=1;∴△MEH、△MHN是等腰三角形,即∠MEH=∠MHE=2∠MNE;∵∠DMN=∠E+∠MNE,故∠DMN=3∠MNE;(3)解:∵∠DMN=45°,∴∠MNE=15°,∠E=30°;Rt△DHE中,DE=2,∠E=30°;∴DH=1,EH=;∴EN=EH+HN=+1;故E(1,+1),根据轴对称性可知,点E在第二象限的对称点(﹣1,+1)也可以.故点E的坐标为:(1,+1)或(﹣1,+1).22.【解答】解:(1)设两次改道的平均增长率为x,根据题意得:100(1+x)2=121,解得:x1=0.1=10%,x2=﹣2.1(舍去).答:两次改道的平均增长率为10%.(2)设乙工程队每天修路y千米,则甲工程队每天修路(y+0.5)千米,根据题意得:=1.5×,解得:y=1,经检验,y=1是原分式方程的解,且符合题意,∴y+0.5=1.5.答:乙工程队每天修路1千米,甲工程队每天修路1.5千米.(3)设甲工程队修路m天,则乙工程队修路(121﹣1.5m)天,根据题意得:0.5m+0.4(121﹣1.5m)≤42.4,解得:m≥




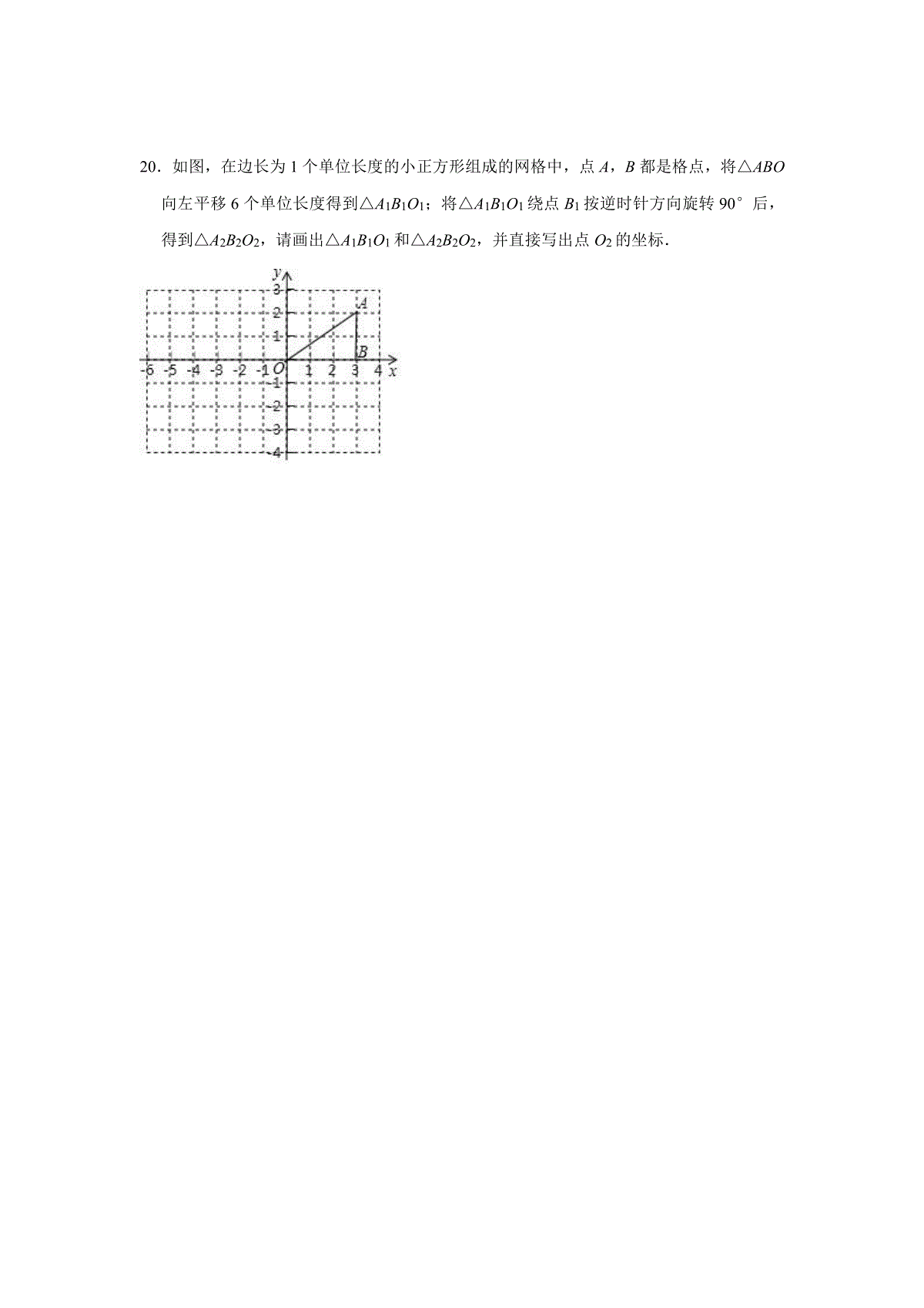
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:四川省南充市2018-2019学年九年级数学上学期期末模拟试卷(pdf,含解析)
链接地址:https://www.777doc.com/doc-8354924 .html