苏教版江苏省宜兴市东坡中学2015届九年级上学期期末考试数学试题(有答案)

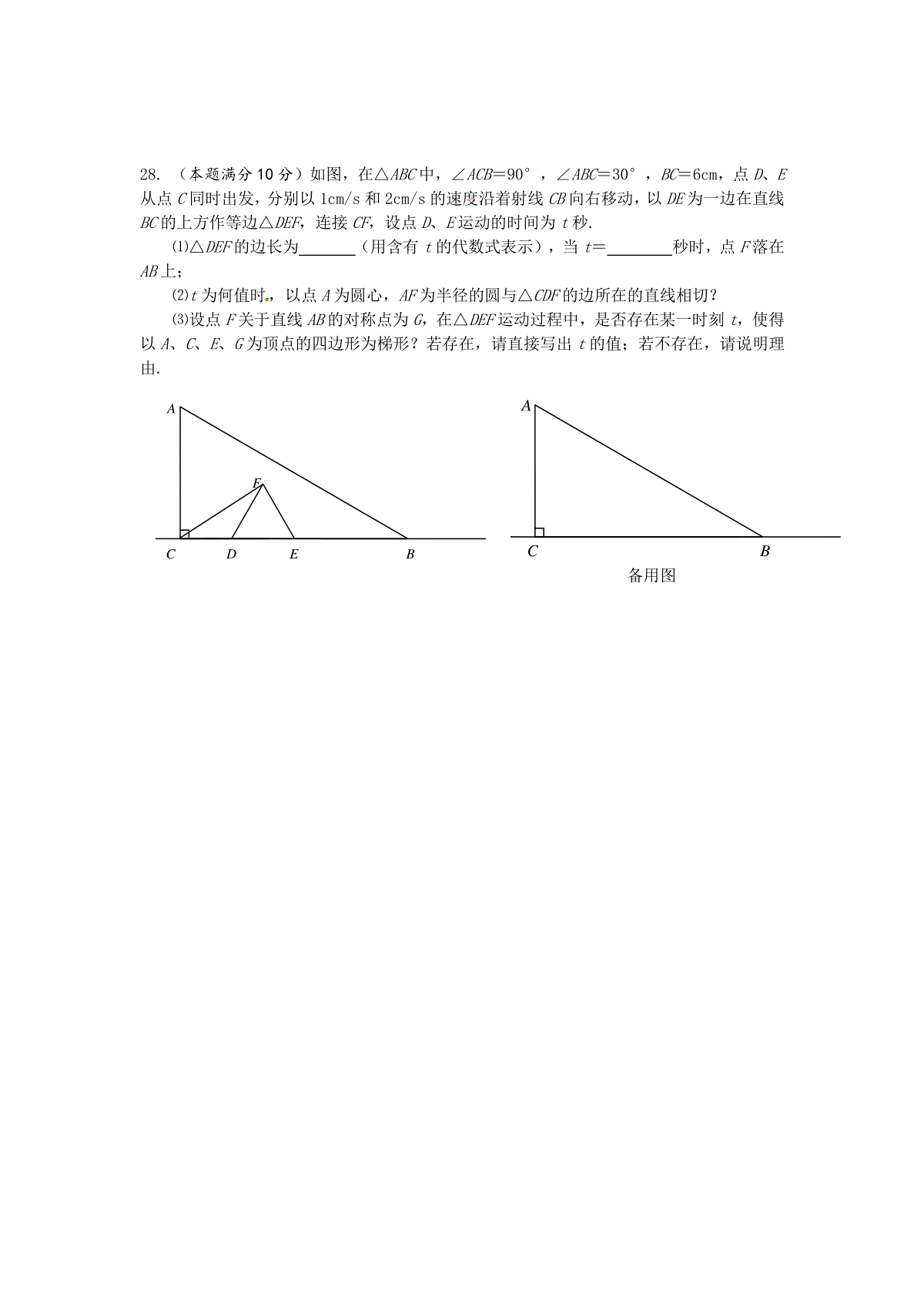
宜兴市东坡中学2014—2015学年第一学期期末考试初三数学一、选择题（本大题共10小题，每小题3分，共30分）323.1.2.7..1abDxCmBA）（式的是下列各式一定是二次根2.下面计算正确的是()A.3333B.3327C.532D.243.已知x＝2是方程32x2－2a＝0的一个解，则2a－1的值是()A．3B．4C．5D．64.如图，AB为圆O的直径，点C在圆O上，若16C,则BOC的度数是（）A.74B.48C.32D.165.抛物线y＝－(x＋2)2－3的顶点坐标是()A．（2，－3）；B．（－2，3）；C．（2，3）；D．（－2，－3）6．已知圆锥侧面展开图的扇形面积为65cm2，扇形的弧长为10cm，圆锥母线长（）A．5cmB．10cmC．12cmD．13cm7.现定义运算“★”，对于任意实数a、b，都有a★b=23aab，如：3★5=32-3×3+5，若x★2=6，则实数x的值是()A．4或1B．4或1C．4或2D．-4或28.在△ABC中，∠C=90°，AC=3cm，BC=4cm．若⊙A，⊙B的半径分别为1cm，4cm，则⊙A与⊙B的位置关系是()A.外切B.内切C.相交D.外离9.竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h＝at2＋bt，其图象如图所示．若小球在发射后第2s第6s时的高度相等，则下列时刻中小球的高度最高的是第()A．3sB．3.5sC．4.2sD．6.5s10.如图，正方形ABCD中，E是BC边上的一点，以E为圆心，EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则EB比EA的值为（）A．53B．54C．33D．[32二﹑填空题（本大题共8小题，每小题2分，共16分）11.方程232xx的两根之积是第9题第10题第15题12.若方程032mxx有两个相等的实数根，则m=13．已知4322xxy，则y=．14.若2m，化简2)2(m。15.如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，若∠BAC=25°，则∠P=__________度.16.如果把抛物线y=2x2向左平移l个单位，同时向上平移4个单位，那么得到的新抛物线的解析式为.17.关于x的方程a（x+m）2+b=0的解是x1=-5，x2=3（a、b、m均为常数，a≠0），则方程a（x+m-2）2+b=0的解是18.如图，图中的圆均为等圆，且相邻两圆外切，圆心的连线构成正三角形，记各阴影部分面积从左到右分别为S1，S2，S3，...则S12:S4的值为三.解答题（本大题共10小题，共84分）19．（本题满分8分）化简与计算：（1）0(π2011)12|32|（2）)483814122(2220．（本题满分8分）解方程：(1)9)12(2x（2）2420xx21.（本题满分6分）如图，实数a、b在数轴上的位置，化简22．（本题满分6分）已知关于x的一元二次方程x2－6x＋k＝0有实数根．（1）求k的取值范围；（2）如果k取符合条件的最大整数，且一元二次方程x2－6x＋k＝0与x2＋mx－1＝0有一个相同的根，求常数m的值．23.（本题满分8分）如图，AB是⊙O的直径，⌒AC＝⌒CD，∠COD＝60°．（1）△AOC是等边三角形吗？请说明理由；（2）求证：OC∥BD．24.（本题满分8分）已知：抛物线与直线y=x+3分别交于x轴和y轴上同一点，交点分别是点A和点C，且抛物线的对称轴为直线x=－2。（1）求出抛物线与x轴的两个交点A、B的坐标。（2）试确定抛物线的解析式。（n+1）个圆22abab第25题（3）观察图象，请直接写出二次函数值小于一次函数值的自变量x的取值范围。25.（本题满分10分）已知，如图，在Rt△ABC中，∠C=90º，∠BAC的角平分线AD交BC边于D。（1）以AB边上一点O为圆心，过A，D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由；（2）若（1）中的⊙O与AB边的另一个交点为E，AB=6，BD=32,求线段BD、BE与劣弧DE所围成的图形面积。（结果保留根号和）26.（本题满分10分）某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和成本进行了调研，结果如下：每件商品的售价M（元）与时间t（月）的关系可用一条线段上的点来表示（如图1），每件商品的成本Q（元）与时间t（月）的关系可用一条抛物线的一部分上的点来表示（如图2）．（说明：图1，图2中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本．）请你根据图象提供的信息回答：（1）每件商品在3月份出售时的利润（利润=售价-成本）是多少元？（2）求图2中表示的每件商品的成本Q（元）与时间t（月）之间的函数关系式；（3）你能求出三月份至七月份每件商品的利润W（元）与时间t（月）之间的函数关系式吗？若该公司共有此种商品30000件，准备在一个月内全部售完，请你计算一下至少可获利多少元？27.（本题满分10分）如图，已知抛物线经过定点．．A（1，0），它的顶点P是y轴正半轴上的一个动点．．，P点关于x轴的对称点为P′，过P′作x轴的平行线交抛物线于B、D两点（B点在y轴右侧），直线BA交y轴于C点．按从特殊到一般的规律探究线段CA与CB的比值：（1）当P点坐标为（0，1）时，写出抛物线的解析式并求线段CA与CB的比值；（2）若P点坐标为（0，m）时（m为任意正实数），线段CA与CB的比值是否与⑴所求的比值相同？请说明理由．ABC备用图28.（本题满分10分）如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，BC＝6cm，点D、E从点C同时出发，分别以1cm/s和2cm/s的速度沿着射线CB向右移动，以DE为一边在直线BC的上方作等边△DEF，连接CF，设点D、E运动的时间为t秒.⑴△DEF的边长为（用含有t的代数式表示），当t＝秒时，点F落在AB上；⑵t为何值时，以点A为圆心，AF为半径的圆与△CDF的边所在的直线相切？⑶设点F关于直线AB的对称点为G，在△DEF运动过程中，是否存在某一时刻t，使得以A、C、E、G为顶点的四边形为梯形？若存在，请直接写出t的值；若不存在，请说明理由.ABCDEF初三数学期末答案1-10:CBCCDDBACA11、3212、4913、4314、m=-215、5016、y=2（x+1）2+417、-3、518、19:719、（1）33（2）16420、（1）-1,2（2）62,6221、21．解：原式=—a—b—（b—a）…………………………3分=—a—b—b+a…………………………5分=—2b………………………622、（1）由⊿=36-4k≥0得k≤9………2分（2）k=9解出方程得x1=x2=338m…………………623、解：（1）△AOC是等边三角形。证明如下：∵⌒AC＝⌒CD，∴∠AOC＝∠COD＝60°。∵OA＝OC，∴△AOC是等边三角形。………………4（2）证明：∵⌒AC＝⌒CD，∴OC⊥AD。又∵AB是⊙O的直径，∴∠ADB＝90°，即BD⊥AD。∴OC∥BD。………………824、解：（1）在y＝x+3中，当y＝0时,x＝3，∴点A的坐标为(－3，0)。当x＝0时,y＝3，∴点C坐标为（0，3）。∵抛物线的对称轴为直线x＝－2，∴点A与点B关于直线x＝－2对称。∴点B的坐标是（－1，0）。………………2（2）∵抛物线的对称轴为直线x＝－2，∴设二次函数的解析式为22yaxc∵二次函数的图象经过点C（0，3）和点A(－3,0)，∴可得方程组：430acac，解得11ac。、∴二次函数的解析式为221yx，即243yxx。………………6[来源:学|科|网]（3）由图象观察可知，当－3＜x＜0时，二次函数值小于一次函数值………………825、（1）如图，作AD的垂直平分线交AB于点O，O为圆心，OA为半径作圆。………………2判断结果：BC是⊙O的切线。连结OD。∵AD平分∠BAC∴∠DAC=∠DAB∵OA=OD∴∠ODA=∠DAB∴∠DAC=∠ODA∴OD∥AC∴∠ODB=∠C∵∠C=90º∴∠ODB=90º即：OD⊥BC∵OD是⊙O的半径∴BC是⊙O的切线。………………6(2)如图，连结DE。设⊙O的半径为r，则OB=6-r，在Rt△ODB中，∠ODB=90º，∴0B2=OD2+BD2即：(6-r)2=r2+(32)2∴r=2∴OB=4∴∠OBD=30º，∠DOB=60º∵△ODB的面积为3223221，扇形ODE的面积为322360602∴阴影部分的面积为32—32。………………1026、解：（1）每件商品在3月份出售时的利润为5元；………………2（2）∵抛物线的顶点坐标为（6，4）∴设抛物线的解析式为Q=a（t-6）2+4∵抛物线过（3，1）点∴1=a（3-6）2+4解得：a=-1/3∴Q=-1/3（t-6）2+4=-1/3t2+4t-8，………………5（3）设每件商品的售价M（元）与时间t（月）之间的函数关系式为M=kt+b∵线段过（3，6）、（6，8）两点∴3k+b=66k+b=8解得：k=2/3，b=4∴M=2/3t+4，所以每件商品的利润W（元）与时间t（月）的函数关系式为W=M-Q=（2/3t+4）-（-1/3t2+4t-8）=1/3t2-10/3t+12∴W=1/3（t-5）2+11/3，∴当t=5时，W的最小值为11/3元∴30000件商品一个月内售完，至少获利30000×11/3=110000元．答：30000件商品一个月内售完，至少获利110000元．………………1027、解：⑴设抛物线的解析式为21(0)yaxa，[来源:学科网ZXXK]抛物线经过A（1，0），∴01,1aa。∴21yx。∵P′、P关于x轴对称，且P（0，1），∴P′点的坐标为（0，-1）。∵P′B∥x轴，∴B点的纵坐标为－1。由21x+1解得，2x。∴B(2，－1)，∴P'B=2。∵OA∥P'B，∴△CP'B∽△COA，∴CAOA12CBPB22………………4。⑵设抛物线的解析式为2(0)yaxma∵抛物线经过A（0，1），∴0,amam＝。∴2ymxm。∵P′B∥x轴，∴B点的纵坐标为m，当ym时，2mxmm，∴220mx。∵0m，∴220mx，∴220x，∴2x。∴B2,m∴P'B=2。同⑴得CAOA12CBPB22。ABCDEFABCDEF∴m为为任意正实数时，CA2CB2。………………1028、（1）边长为t，t=2………………………………………………………4分（2）[来源:学科网ZXXK]①当⊙A与DF相切，t=2………………………………………………………5分②当⊙A与CD相切，t=2………………………………………………………6分③当⊙A与CF相切，t=1………………………………………………………7分（3）①t=1.5②t=1③t=3212………………………………………………………10分