当前位置:首页 > 中学教育 > 高中教育 > 重庆市七校联考2016-2017学年(上)高一期末数学试题(无答案)
2016-2017学年(上)期末七校联考高2019级数学试题____班、姓名____一.选择题:(每小题5分,共60分)1.67cos的值为()A.21B.21C.23D.232.已知集合21,M,4,3,2N,若NMP,则P的子集个数为()A.14B.15C.16D.323.已知函数001)(xaxxxxf,,,若)1()1(ff,则实数a的值为()A.1B.2C.0D.14.若函数01)(2abxaxxf是定义在R上的偶函数,则函数32()gxaxbxx是()A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数5.设312loga,3)21(b,213c,则()A.abcB.cbaC.bacD.cab6.已知32)tan(,21)6tan(,则)6tan(等于()A.41B.87C.81D.977.方程3log21xx和3log31xx的根分别为、,则有()A.B.C.D.无法确定与大小8.函数62sin2)(xxf的图像为M,则下列结论中正确的是()A.图像M关于直线12x对称B.由xy2sin2的图像向左平移6得到MC.图像M关于点0,12对称D.)(xf在区间125,12上递增9.函数)4(sin2xy的图像沿x轴向右平移m个单位0m,所得图像关于y轴对称,则m的最小值为()A.B.43C.2D.410.定义在R上的偶函数)(xf在区间)0,(上单调递减,若实数a满足)3()3(12ffa,则a的取值范围是()A.,4143,B.43,C.,41D.41,4311.已知232,,0,2,且02sin23,01cos2823,则2sin的值为()A.0B.22C.21D.112.若区间21,xx的长度定义为12xx,函数0,1)(22mRmxmxmmxf的定义域和值域都是ba,ab,则区间ba,的最大长度为()A.332B.33C.3D.3二.填空题:(每小题5分,共20分)13.计算:038125lg4lg27log_____________14.已知扇形的面积为42cm,扇形的圆心角为2弧度,则扇形的弧长为____________15.若,0,且4sin2cos21,则2sin的值为____________16.已知正实数33223,1(,)()xyxyxyfxyxy,且,若,则),(yxf的值域为____________三.解答题:17.(本小题满分10分)已知全集RU,函数xxxf10lg3)(的定义域为集合A,集合}75|{xxB.(1)求A集合;(2)求ABCU)(.18.(本小题满分12分)在平面直角坐标系xoy中,若角的始边为x轴的非负半轴,其终边经过点4,2P.求tan的值;(2)求4sin212cos2sin22的值.19.(本小题满分12分)已知二次函数14)(2xmxxf,且满足)3()1(ff.(1)求函数)(xf的解析式;(2)若函数)(xf的定义域为2,2,求)(xf的值域.20.(本小题满分12分)已知函数)4sin()4sin(sincos32sin)(2xxxxxxf0,且)(xf的最小正周期为.(1)求的值;(2)求函数)(xf在区间,0上的单调增区间.21.(本小题满分12分)已知函数21()log()21mxfxxx是奇函数为常数m.(1)判断函数)(xf在),21(x上的单调性,并用定义证明你的结论;(2)若对于区间5,2上的任意x值,使得不等式nxfx2)(恒成立,求实数n的取值范围.22.(本小题满分12分)已知函数4()(sincos)sin219fxaxxx,若9132)4(f.(1)求a的值,并写出函数)(xf的最小正周期(不需证明);(2)是否存在正整数k,使得函数)(xf在区间k,0内恰有2017个零点?若存在,求出k的值,若不存在,请说明理由.2016-2017学年(上)期末七校联考高2019级数学试题参考答案一、选择题:1-6:DCBABC7-12::ACDABA二.填空题:13.2914.cm415.116.1,41三、解答题17.解:(1)由题意可得:01003xx,则103|xxA…………5分(2)75|xxxBCU或…………8分10753|)(xxxABCU或…………10分18.解:(1)由任意角三角函数的定义可得:x=2,y=4,故224tan…………6分(2)cossincossin2原式…………8分1tan1tan2…………10分351214…………12分19.解:(1))3()1(ff由可得该二次函数的对称轴为1x…………2分即124m,从而得2m…………4分亦可直接)3()1(ff由得2m所以该二次函数的解析式为142)(2xxxf…………6分(2)由(1)可得312)(2xxf,对称轴为1x…………9分所以()2,215,3fx在上的值域为…………12分20.解:(1)xxxxf2cos212sin322cos1)(…………3分2162sin2x…………5分由题意得22,可得1…………6分(2)由(1)知2162sin2)(xxf,则由函数单调递增性可知:Zkkxk,226222,整理得Zkkxk,36…………9分取1k与0,取交集,得到增区间3,0;取2k与0,取交集,得到增区间,65;而当0k或3k时与0,无交集,所以,0)(在xf上的增区间为3,0,,65…………12分21.解:(1)由条件可得0)()(xfxf,即0121log121log22xmxxmx,化简得222411xxm,从而得2m;当2m时,)(xf定义域为空集,舍去,而当2m时,221()log21xfxxx符合题意…………2分又22212()loglog12121xfxxxxx,故,21)(xxf在上为单调减函数………3分用定义证明如下:设121,(,)2xx,且12xx则1212122122221121221212121()()loglog=log()21212121xxxxfxfxxxxxxxxx因为2121xx,所以012xx,12210,210xx又因为121221(21)(21)(21)(21)4()0xxxxxx,12210,210xx所以可得1212212112121xxxx,所以1222122121loglog102121xxxx所以0)()(21xfxf,即)()(21xfxf;所以)(xf在,21x上为单调减函数………7分法二:11222122121()()=log()2121xfxfxxxx,因为2121xx,所以1122212122110122121121xxxx,所以12222121loglog102121xx,(2)设xxfxg2)()(,由(1)得)(xf在,21x上为单调减函数,所以xxfxg2)()(在5,2上单调递减;所以xxfxg2)()(在5,2上的最大值为6log2352g…………10分由题意知xgn在5,2上的最大值,所以6log352n…………12分121()log11()(1,)12[3,4],()(),2xaxfxxafxxfxmm设奇函数,()求的值,并判断在的单调性类;()若对于上的每一个值不等式恒成立求实数的取题:值范围.11222221122112121211()()loglog---------111110111.--------3111211()loglog(1)---------411211(2)1()()log21axaxfxfxxxaxxaxxaxaxxaafxxxxxxfxfxx,分,分检验(舍去),:,故分则解设2,-------51分112122111222min211221100-------6(0,1)------721111211log0()()()(1,)---------2111(3)()()()()--------92()[3,4]--xxxxxxxxfxfxyfxxgxfxgxmgx,分,分,故,所以,在内单调递增.8分依题意有,令,则分易知在是单调函数,min-------9()(3).89[3,4]---------8gxgm10分时,原不等式在上恒成立.12分22.解:(1)413()212499fa,故1a……………2分又44()sin()cos()sin2()1sincossin2199fxxxxxxx所以,()()fxfx,所以T是()fx的一个周期(2)存在n=504,满足题意,理由如下:…………5分当2,0x时,4()sincossin219fxxxx,设sincos2sin()4txxx,则2,1t,且12sin2tx,则245()099fxtt,可得1t或45t,由sincos2sin()4txxx图像可知,x在2,0上有4个零点满足题意………8分(注:2sin()10,42txx,5552sin()arcsinarcsin44444242txxx或者,共4个零点)当),2(x时,4()sincossin219fxxxx,sincos2sin()4txxx,则2,1t,且212sintx,2413()099fxtt,1t或413t,因为2,1t,所以1t或413t舍去,所以x在,2上不存在零点。……………10分综上讨论知:函数)(xf在,0上有4个零点,而2017=41504,因此函数在0,504有4504=2016个零点,而(2017)()0ff,因此函数在504,0有2017个零点,所以存在正整数504k满足题意。……………12分
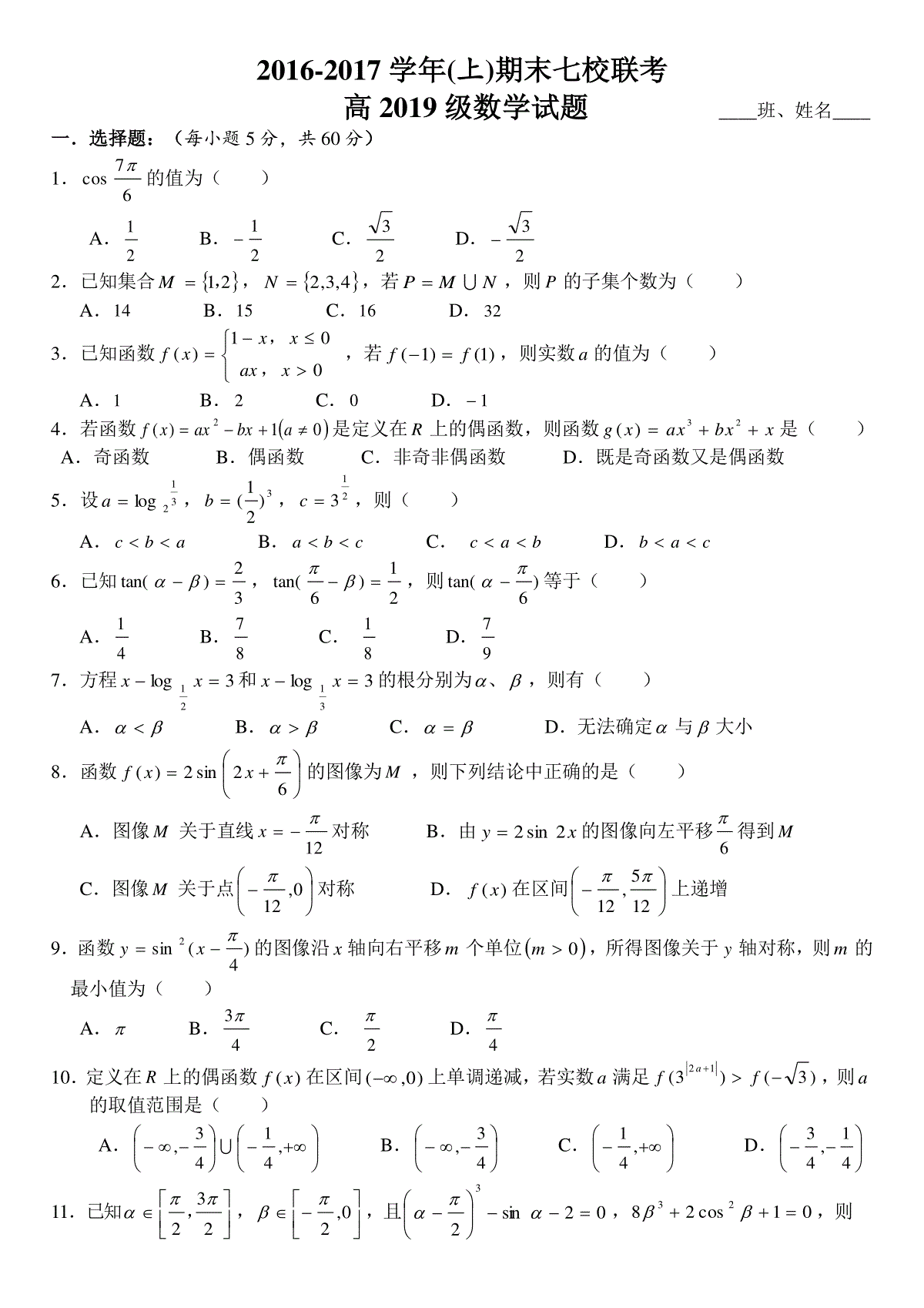

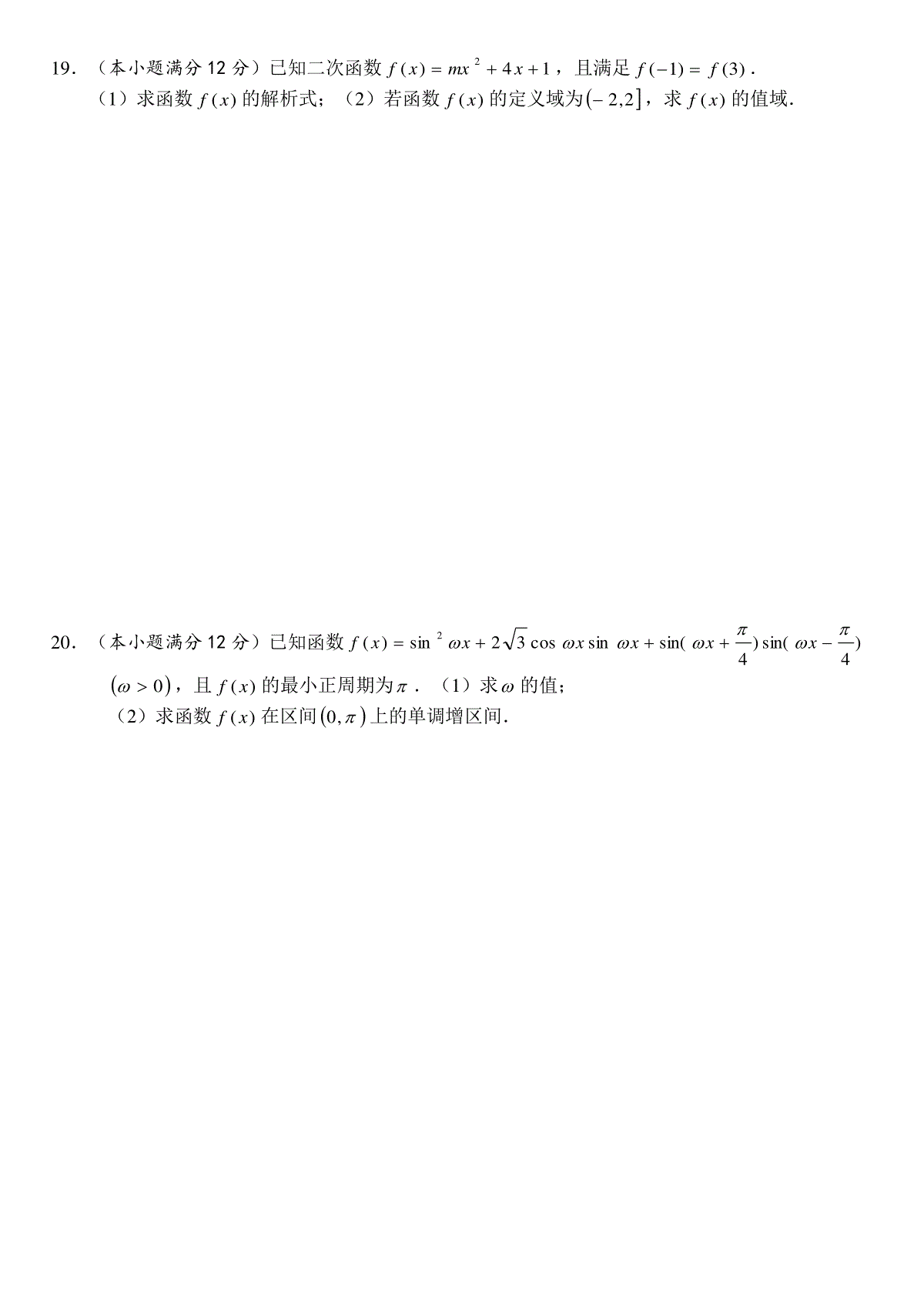


 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:重庆市七校联考2016-2017学年(上)高一期末数学试题(无答案)
链接地址:https://www.777doc.com/doc-2202445 .html