当前位置:首页 > 临时分类 > 2014-2015高考理科数学《函数的图象》练习题
-----欢迎登陆明师在线浏览更多的学习资讯!-----2014-2015高考理科数学《函数的图象》练习题[A组基础演练·能力提升]一、选择题1.函数f(x)=log12cosx-π2xπ2的图象大致是()解析:因为f(-x)=log12cos(-x)=log12cosx=f(x),所以函数f(x)为偶函数,排除A、B;又fπ3=log12cosπ3=log1212=1,故排除D,应选C.答案:C2.(2014年广州模拟)函数y=|x|axx(a1)的图象的大致形状是()解析:由题意知,y=|x|axx=ax,x0-ax,x0,又a1,所以由y=ax的图象可知,B选项符合题意.答案:B3.如图,半径为2的⊙O与直线MN相切于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交⊙O于点Q,设∠POQ为x,弓形PmQ的面积为S=f(x),那么f(x)的图象大致是()解析:利用函数的凹凸性可知选D.答案:D-----欢迎登陆明师在线浏览更多的学习资讯!-----4.已知函数f(x)=3xxlog13xx,则函数y=f(1-x)的图象大致是()解析:由f(x)=3xxlog13xx,得f(1-x)=31-xxlog13-xx.因此,x≥0时,y=f(1-x)为减函数,且y0;x0时,y=f(1-x)为增函数,且y0.故选C.答案:C5.对实数a和b,定义运算“⊗”:a⊗b=a,a-b≤1,b,a-b1.设函数f(x)=(x2-2)⊗(x-1),x∈R.若函数y=f(x)-c的图象与x轴上恰有两个公共点,则实数c的取值范围是()A.(-1,1]∪(2,+∞)B.(-2,-1]∪(1,2]C.(-∞,-2)∪(1,2]D.[-2,-1]解析:令(x2-2)-(x-1)≤1,得-1≤x≤2,∴f(x)=x2--1≤xx-x-1或x,∵y=f(x)-c与x轴恰有两个公共点,画出函数的图象得知实数c的取值范围是(-2,-1]∪(1,2].故选B.答案:B6.已知函数f(x)的图象向左平移1个单位长度后关于y轴对称,当x2x11时,[f(x2)-f(x1)](x2-x1)0恒成立,设a=f-12,b=f(2),c=f(3),则a,b,c的大小关系为()A.cabB.cbaC.acbD.bac解析:由题意得f(x+1)的图象关于y轴对称,则f(x)的图象关于x=1对称,满足f(x)=f(2-x),∴a=f-12=f52.又由已知得f(x)在(1,+∞)上为减函数,∴f(2)f52f(3),即bac.答案:D二、填空题7.直线y=1与曲线y=x2-|x|+a有四个交点,则a的取值范围是________.-----欢迎登陆明师在线浏览更多的学习资讯!-----解析:如图,作出y=x2-|x|+a的图象,若要使y=1与其有4个交点,则需满足a-141a,解得1a54.答案:1,548.已知函数y=f(x)(x∈R)满足f(x+1)=f(x-1),且x∈[-1,1]时,f(x)=x2,则函数y=f(x)与y=log5x的图象交点的个数为________.解析:根据f(x+1)=f(x-1),得f(x)=f(x+2),则函数f(x)是以2为周期的函数,分别作出函数y=f(x)与y=log5x的图象(如图),可知函数y=f(x)与y=log5x的图象的交点个数为4.答案:49.已知函数f(x)=2x,x≥2,x-3,x2.若关于x的方程f(x)=k有两个不同的实根,则实数k的取值范围是________.解析:当x2时,f′(x)=3(x-1)2≥0,说明函数在(-∞,2)上单调递增,函数的值域是(-∞,1),又函数在[2,+∞]上单调递减,函数的值域是(0,1].因此要使方程f(x)=k有两个不同的实根,则0k1.答案:(0,1)三、解答题10.若直线y=2a与函数y=|ax-1|(a0且a≠1)的图象有两个公共点,求a的取值范围.解析:当0a1时,y=|ax-1|的图象如图(1)所示,-----欢迎登陆明师在线浏览更多的学习资讯!-----由已知得02a1,∴0a12.当a1时,y=|ax-1|的图象如图(2)所示.由已知可得02a1,∴0a12,但a1,故a∈∅.综上可知,a的取值范围:0,12.11.已知函数f(x)=x|m-x|(x∈R),且f(4)=0.(1)求实数m的值;(2)作出函数f(x)的图象;(3)根据图象指出f(x)的单调递减区间;(4)根据图象写出不等式f(x)0的解集;(5)求当x∈[1,5)时函数的值域.解析:(1)∵f(4)=0,∴4|m-4|=0,即m=4.(2)f(x)=x|4-x|=xx-=x-2-4,x≥4,-xx-=-x-2+4,x4.f(x)的图象如图所示.(3)f(x)的单调递减区间是[2,4].(4)由图象可知,f(x)0的解集为{x|0x4,或x4}.(5)∵f(5)=54∴由图象知,函数在[1,5)上的值域为[0,5).12.(能力提升)已知定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且对x∈R,恒有f(x+1)≥f(x),求实数a的取值范围.解析:当x≥0时,f(x)=|x-a2|-a2-----欢迎登陆明师在线浏览更多的学习资讯!-----=-x,0≤x≤a2,x-2a2,xa2.因为函数f(x)为奇函数,故函数f(x)的图象关于原点对称,如图所示.因为f(x+1)的图象可以看作由函数f(x)的图象向左平移1个单位得到,需将函数f(x)的图象至少向左平移4a2个单位才能满足不等式f(x+1)≥f(x)恒成立,所以4a2≤1,故a∈-12,12.[B组因材施教·备选练习]1.(2014年济南模拟)函数f(x)=lnx-1x的图象是()解析:自变量x满足x-1x=x2-1x0,当x0时可得x1,当x0时可得-1x0,即函数f(x)的定义域是(-1,0)∪(1,+∞),据此排除选项A、D.函数y=x-1x单调递增,故函数f(x)=lnx-1x在(-1,0),(1,+∞)上单调递增,故选B.答案:B2.函数f(x)=log3x,x0,cosπx,x0的图象上关于y轴对称的点共有()A.0对B.1对C.2对D.3对解析:因为y=cosπx是偶函数,图象关于y轴对称.所以,本题可转化成求函数y=log3x与y=cosπx图象的交点个数的问题.作函数图象如图,可知有三个交点,即函数f(x)图象上关于y轴对称的点有3对.-----欢迎登陆明师在线浏览更多的学习资讯!-----答案:D3.设方程3x=|lg(-x)|的两个根为x1,x2,则()A.x1x2<0B.x1x2=1C.x1x2>1D.0<x1x2<1解析:函数y=3x与函数y=|lg(-x)|的图象如图所示,由图示可设x1<-1<x2<0,则0<3x1<3x2<1,且3x1=-x1,3x2=-lg-x2,可得3x1-3x2=lg(-x1)+lg(-x2)=lgx1x2,∵3x1-3x2<0,∴0<x1x2<1,故应选D.答案:D
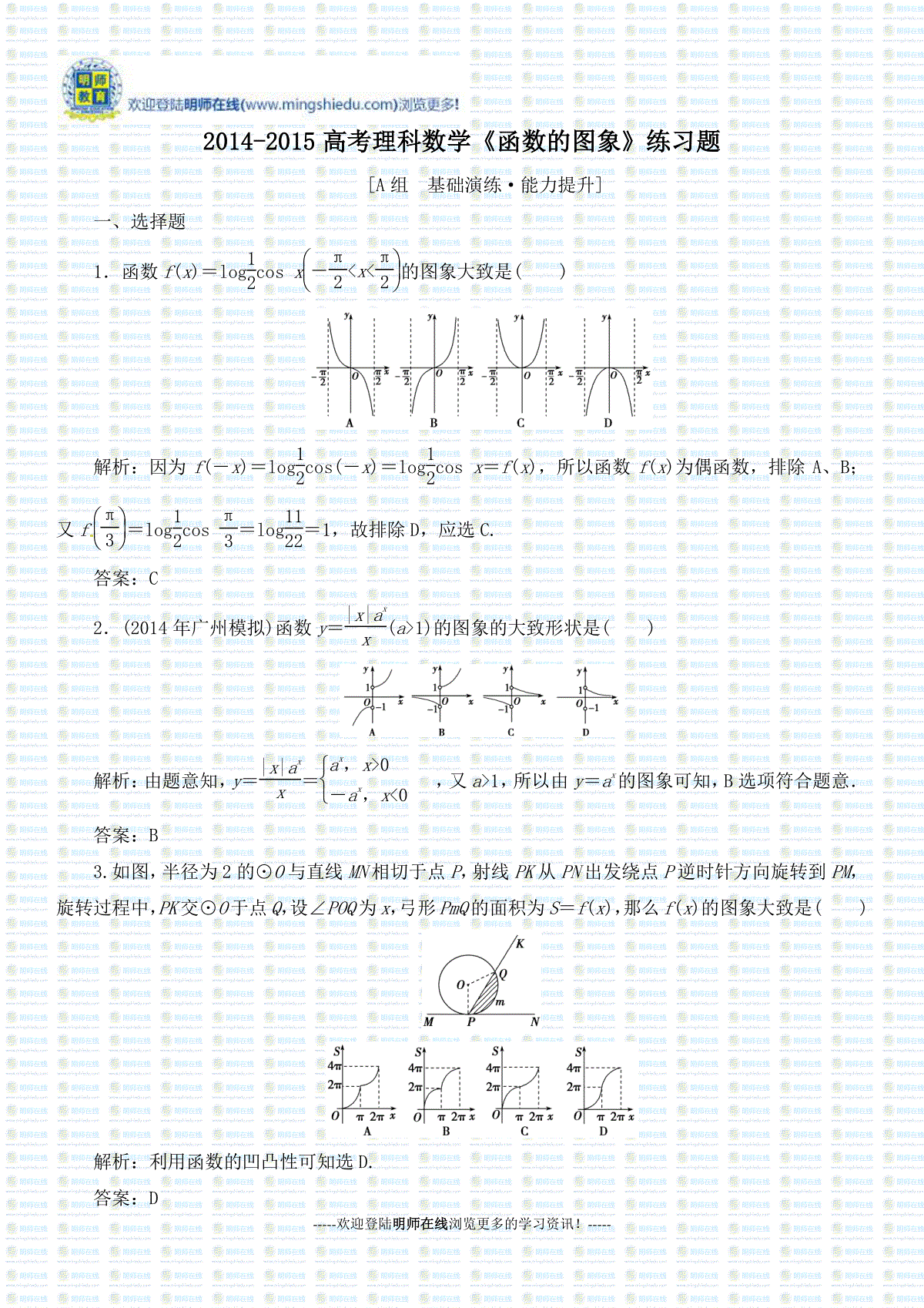
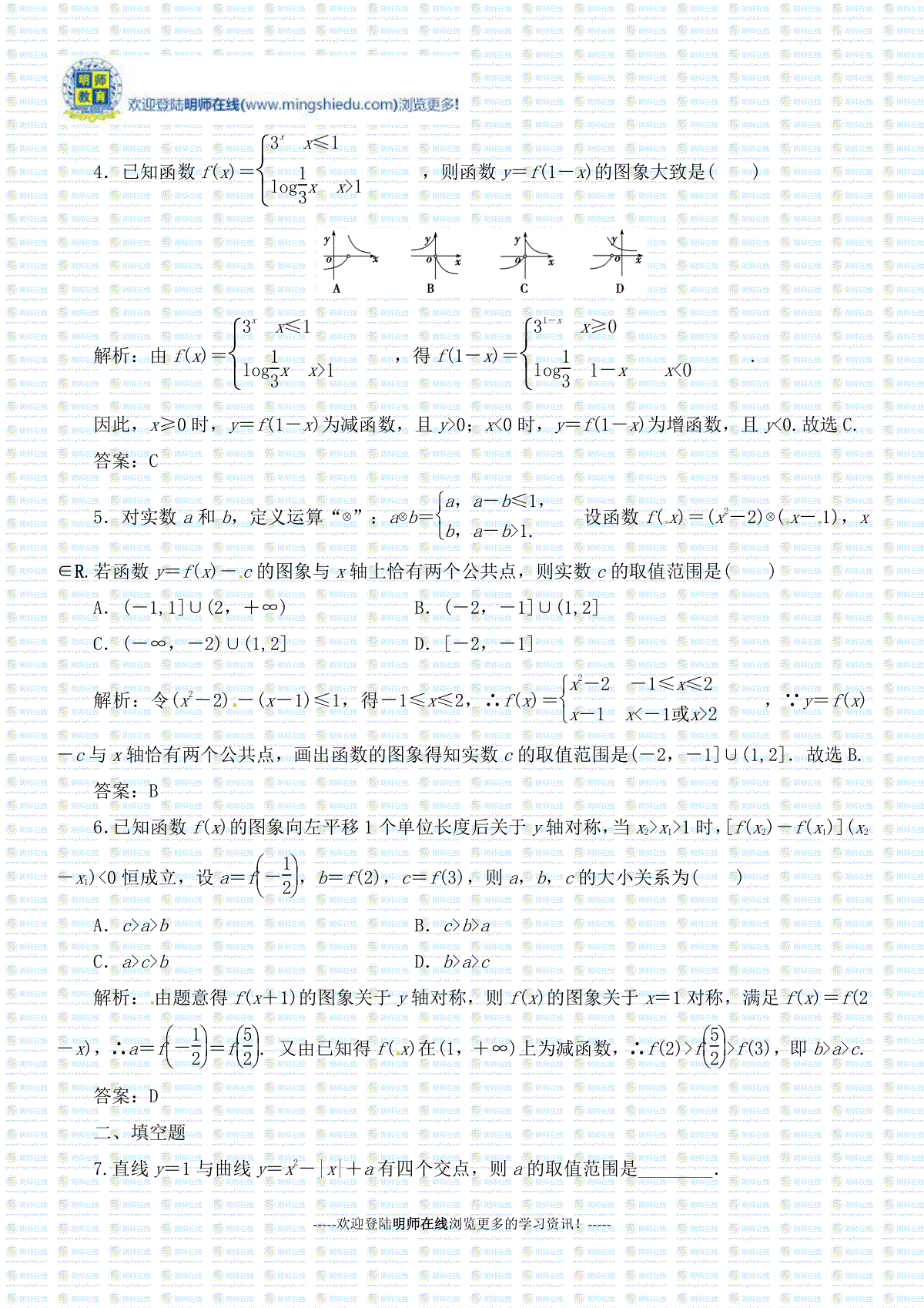


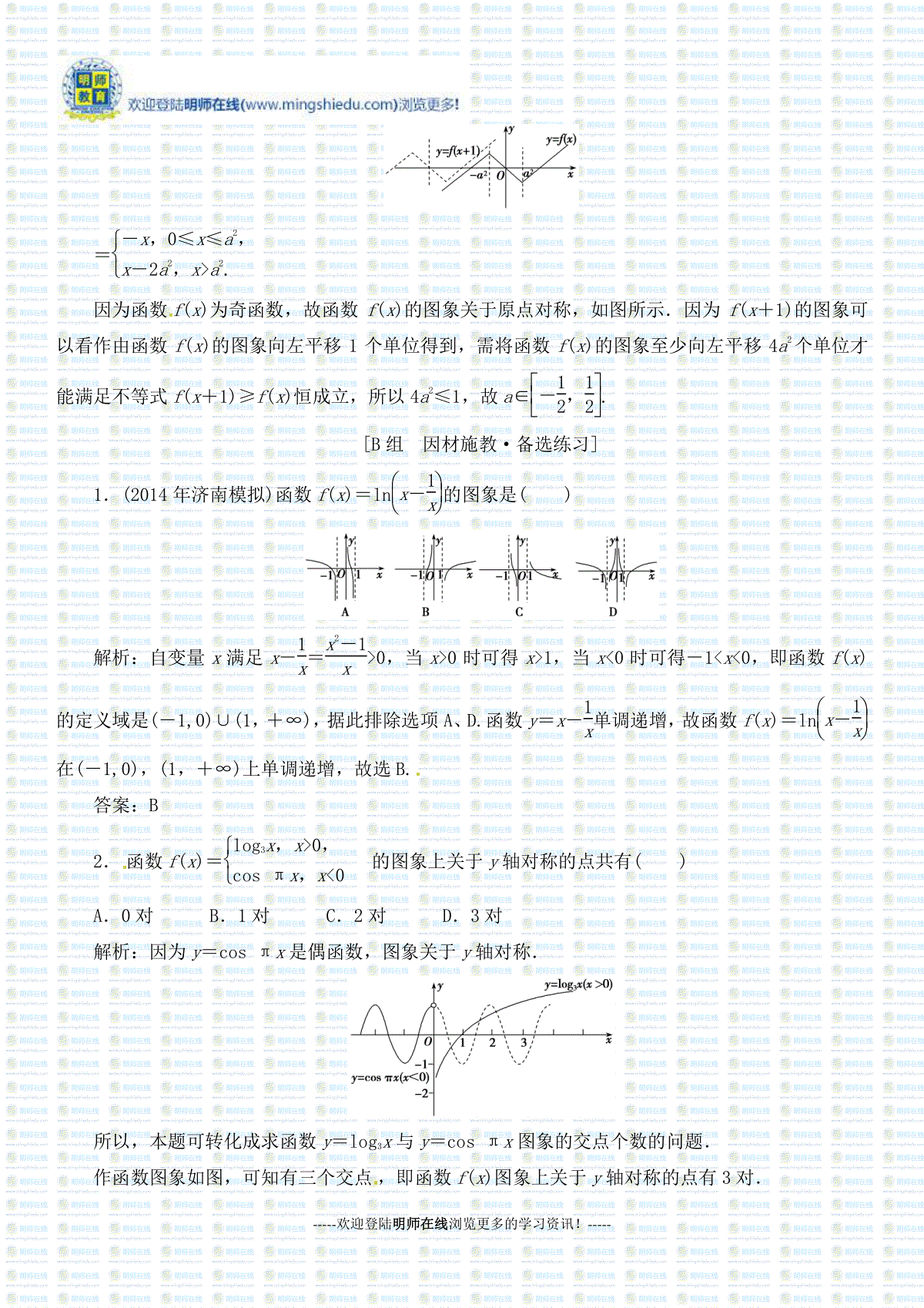
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:2014-2015高考理科数学《函数的图象》练习题
链接地址:https://www.777doc.com/doc-2958127 .html