当前位置:首页 > 电子/通信 > 电子设计/PCB > 12-13期中测试题答案1
第1页共5页上海海洋大学期中试卷答案学年学期2009~2010学年第2学期考核方式闭卷课程名称概率论与数理统计课程号学分4学时题号一二三四五六七八九十总分分数阅卷人姓名:学号:专业班名:一.填空题(每小题3分,共30分)。1.甲、乙两人各射击一次,事件A,B分别表示甲、乙射中,则BA表示甲乙都未射中。2.设A、B为任意两个随机事件,设4.0)A(p,3.0)B(p,6.0)B(pA,则)B(pA0.9。3.总经理的5位秘书中有2位精通外语,今偶遇其中3位秘书,则其中恰有一位精通外语的概率为53。4.随机事件A、B满足5.0)A(p,6.0)B(p,若8.0)AB(p,则)B(pA0.7。5.随机事件1A、2A、3A、4A相互独立,且)4,3,2,1(11)(AiiPi,则)AAA(A4321P54。6.若随机变量X的概率分布为参数为的泊松分布,且有)4()2(XPXP,则32。7.一袋中有两个黑球和若干个白球,现有放回地摸球4次,若至少摸到一个白球的概率为8180,则袋中白球数为4。8.设随机变量N(1,4)~X,0.6915(0.5),0.9332(1.5),则)2(XP0.3753。9.若相互独立n21X,,X,X且分别服从正态分布),(2iiN,则~1niiiXa),(2121iniiniiiaaN。10.设随机变量),N(~X2,则随着的增大,概率)3XP(的值不变(填变大、变小、或者不变)。二、选择题(每小题3分,共30分)1.若BA,则(C)A))((A)BPPB)0)(ABPC)B未发生则A必不发生D)B发生则A可能不发生第2页共5页2.下列概率的性质中不属于概率的公理化定义的是(C)。(A)1)A(P0(B)0)P(,1)(P(C))A(P1)A(P(D)若j)(iAAji,则1iii1i)A(P)A(P3.若随机变量X的概率密度函数为)x(-)x(f,则(D)成立。(A)01dx)x(f(B)1dx)x(fx(C)1)x(f0(D)0)x(f4.函数其他00xe)x(fx-是(A)的概率密度。(A)指数分布(B)柯西分布(C)瑞利分布(D)超几何分布5.设)xX(P)x(F是连续型随机变量X的分布函数,则下列结论中错误的是(A)。(A))x(F是递减函数(B))x(F是不减函数(C))x(F是右连续的(D)1)F(,0)(F6.若随机变量X的概率密度函数其它01x0x4)x(f3,则X的分布函数为(D)。(A)其他01x0x12)x(F2(B)0x01x0x121x1)x(F2(C)其他01x0x)x(F4(D)0x01x0x1x1)x(F47.设随机变量),25,(~),16,(~NYNX记,)5(,)4(21pYPpXP则(A)A)对任意实数,均有21pp;B)对任意实数,均有21ppC)对任意实数,均有21pp;D)对个别实数,才有21pp8.设随机变量),,(~2NX,其密度函数为644261)(xxexf,则下列正确的是(D)A)3,42B)6,22C)6,42D)3,229.若),,,,(~),(222121NYX,则YX,相互独立的充要条件是(D)A)0;B)0;C)0;D)010.在随机变量的可加性叙述中,下列错误的是(A)。(A)),p,n(B~Y),p,n(B~X2211相互独立,且YX,则)pp,nn(B~YX2121(B)),(P~Y),(P~X21相互独立,且YX,则)(P~YX21第3页共5页(C)),,(N~Y),,(N~X222211相互独立,且YX,则),(N~YX222121(D)),p,(~Y),p,(~nBnBX相互独立,且YX,则),2(~YpnBX三、计算题(每小题10分,共40分)1、(10分)对以往的数据分析结果表明,当机器调整良好时,产品的合格率为98%,而当机器发生某种故障时,其合格率为55%,每天早上机器开动时,机器调整良好的概率为95%,试求已知某日早上第一件产品是合格品时,机器调整良好的概率是多少?解:令A表示事件“产品合格”,B表示事件“机器调整良好”则有05.0)(,95.0)(,55.0)(,98.0)(BPBPBAPBAP所求概率为97.005.055.095.098.095.098.0)()()()()()()(BPBAPBPBAPBPBAPABP2、(20分)设随机变量X的概率密度为.010),1()(其它,;当xxaxxf,试求:(1)常数a;(2)X的分布函数;(3)E(X),D(X);(4)XDXEX(2)(P。解:(1)101()(1)6afxdxaxxdx6a(2)6(1),01()0.xxxfx当;,其它2300,0;0,0;()6(1),01;32,01;1,1.1,1.xxxFxttdtxxxxxx(3)10E(X)=()6(1)0.5xfxdxxxxdx22222D(X)=E(X)-(E(X))E(X)-0.5()0.25xfxdx1206(1)0.250.05xxx(4)P()2(P0.520.05XEXDXX{0.520.050.520.05}PX22(0.520.05)(0.520.05)3[(0.520.05)(0.520.05)]FF332[(0.520.05)(0.520.05)]0.984第4页共5页2.(10分)设顾客排队等待服务的时间X(以分计)服从51的指数分布,某顾客等待服务,若超过10分钟,他就离开,他一个月要去等待服务5次,以Y表示一个月内他未等到服务而离开的次数,试求Y的分布和)0(YP。解:根据题意,得10))P(XB(5,~Y——2分已知X的密度函数为,0,51f(x)51xe0x0x——3分所以,102515110)P(Xedxex,所以)B(5,~Y2e,即)5,4,3,2,1,0()e-(1Ck)P(Yk522k5kek——8分52)e-(111)P(Y——10分3.(10分)已知随机变量X的分布函数为)(arctan)(xxBAxF。试求:(1)系数A与B;(2)X落在(1,1)内的概率。解:(1)因为12)(,02BA)F(-BAF解方程组得,1,21BA——5分(2)因为xxFarctan121)(所以21))4(121()4121()1()1()11(FFXP——5分4.(10分)设随机变量X的密度函数为,,01)(Xxxf其他11x,求随机变量1XY2的分布函数和密度函数解:对Ry,有)1()1()(F22YyXPyXPy——1分1)当1y时,0)1()1()(F22YyXPyXPy;——2分2)当1y时,)1()1()(F2YyXPyXPy——3分a)当2y时,dxxdxxyXPyXPyyyy10112Y)1(2)1()1()1()(F11-y2y——5分第5页共5页b)当2y时,1)1()1()1()(F112YdxxyXPyXPy——7分所以11120)(FYyyy1y2y11y——8分对Ry,密度函数0111)()(f/YyyFyY其他21y——10分




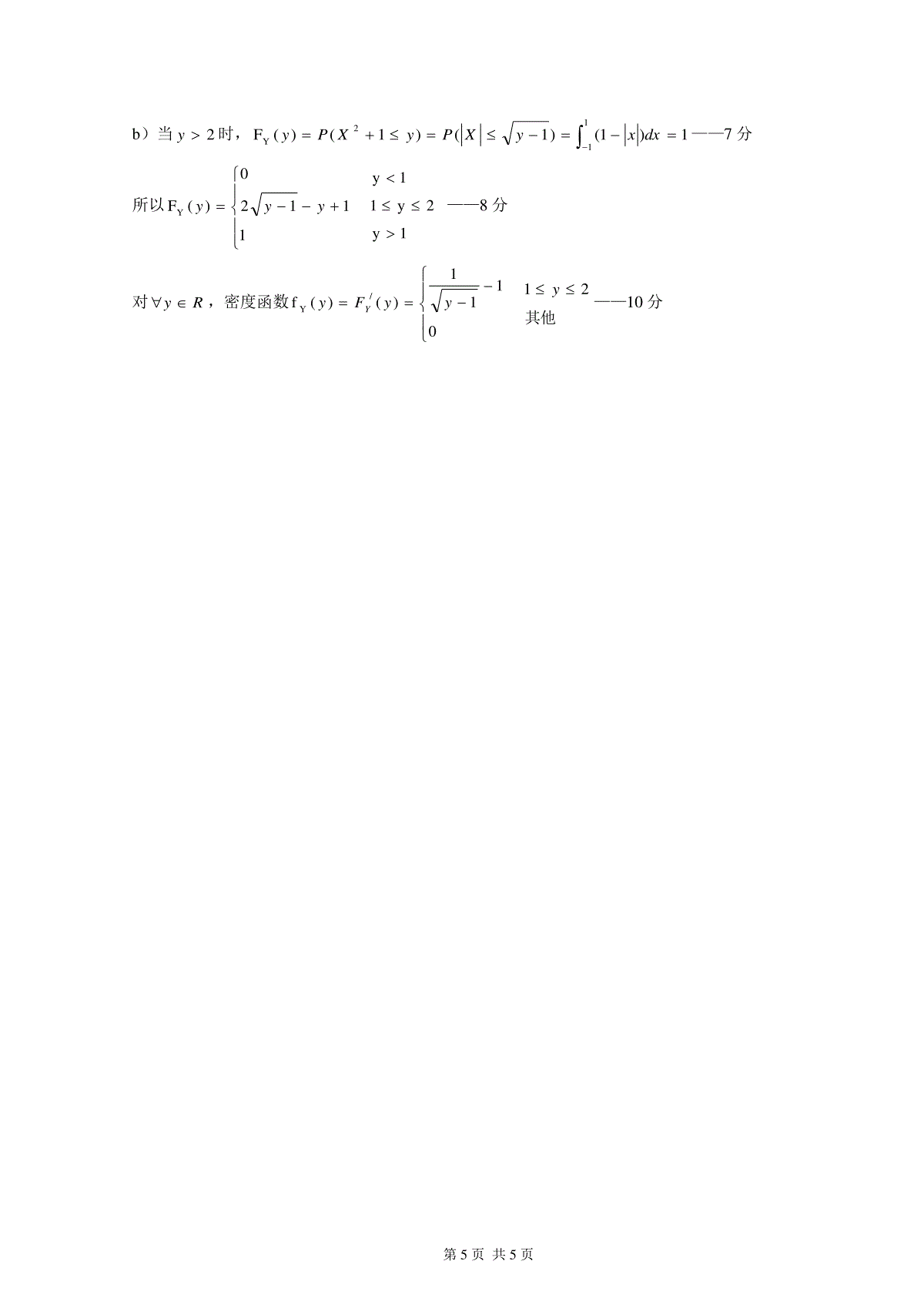
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:12-13期中测试题答案1
链接地址:https://www.777doc.com/doc-3096894 .html