【全国市级联考word】江苏省常熟市2017-2018学年高二上学期期中考试数学试题

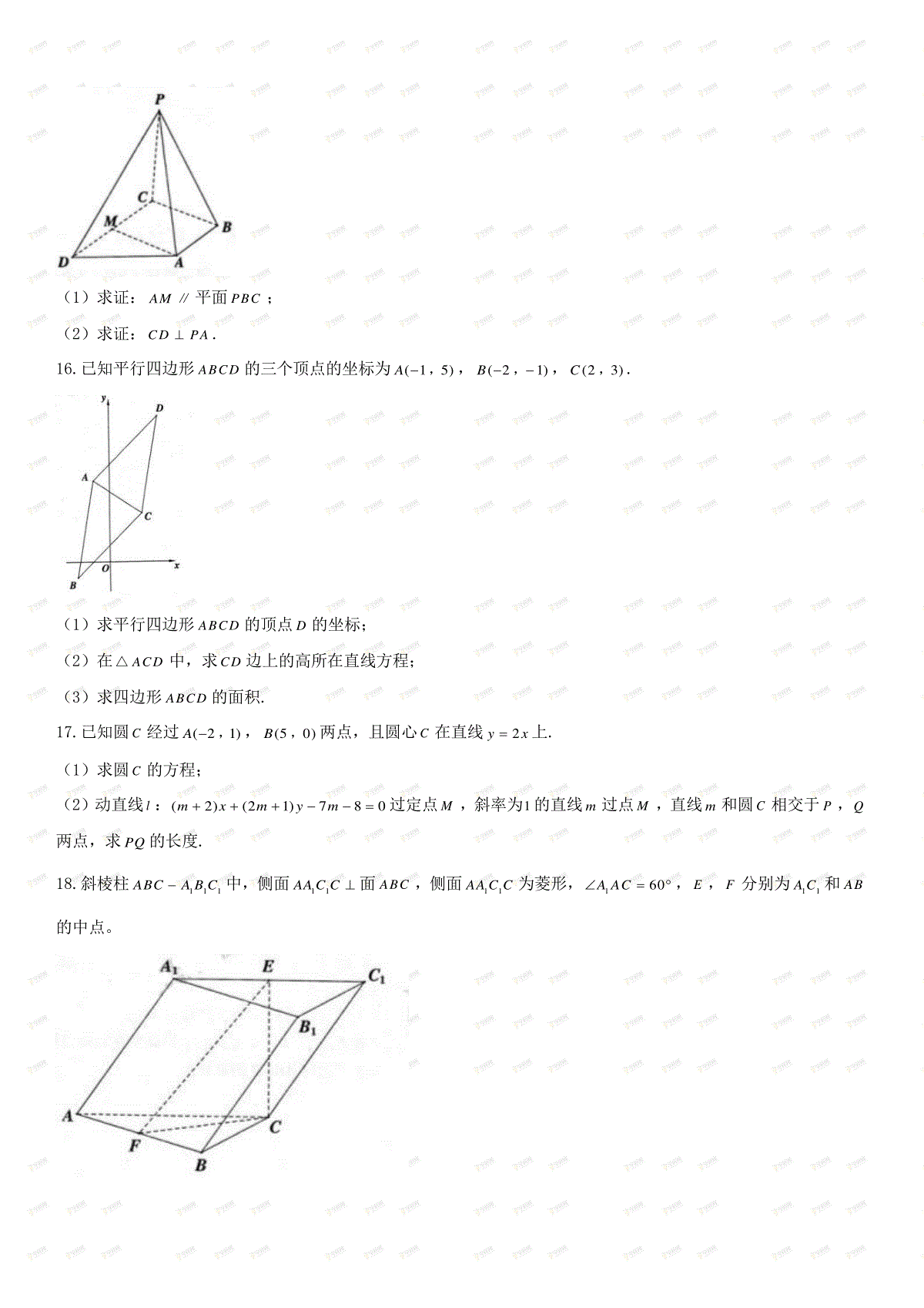
2017-2018学年第一学期期中试卷高二数学第一卷一、填空题：本大题共14小题，每小题5分，共70分.请把答案填写在答题卷相应位置上．．．．．．．．.1.已知直线l的斜率为1，则它2220xyxy的倾斜角为．2.已知圆C的方程为，则它的圆心坐标为．3.若直线a和平面平行，且直线b，则两直线a和b的位置关系为．4.已知直线1l：310axy和2l：2(1)10xay垂直，则实数a的值为．5.已知直线240xy和坐标轴交于A、B两点，O为原点，则经过O，A，B三点的圆的方程为．6.一个圆锥的侧面展开图是半径为3，圆心角为2π3的扇形，则这个圆锥的高为．7.已知P，Q分别为直线390xy和310xy上的动点，则PQ的最小值为．8.已知m，n是空间两条不同的直线，，是两个不同的平面，下面说法正确的有．①若m，m，则；②若m，n，，则mn；③若m，n，∥，则mn∥；④若m∥，m，n，则mn∥.9.直线210xy关于直线1x对称的直线方程为．10.已知底面边长为1，侧棱长为2的正四棱柱，其各顶点均在同一个球面上，则该球的体积为．11.若直线1l：yxa和2l：yxb将圆22(1)(2)8xy分成长度相同的四段弧，则ab．12.已知正三棱锥的体积为933cm，高为3cm，则它的侧面积为2cm．13.已知(12)A，，(31)B，，若圆222xyr（0r）上恰有两点M，N，使得MAB△和NAB△的面积均为5，则r的范围是．14.已知线段AB的长为2，动点C满足CACB（为常数，1），且点C始终不在以B为圆心12为半径的圆内，则的范围是．第二卷二、解答题：本大题共6小题，共90分.请在答题卷指定区域内作答，．．．．．．．．．．．解答应写出文字说明、证明过程或演算步骤.15.四棱锥PABCD中，PDPC，底面ABCD为直角梯形，ABBC，ABCD∥，2CDAB，点M为CD的中点.（1）求证：AM∥平面PBC；（2）求证：CDPA.16.已知平行四边形ABCD的三个顶点的坐标为(15)A，，(21)B，，(23)C，.（1）求平行四边形ABCD的顶点D的坐标；（2）在ACD△中，求CD边上的高所在直线方程；（3）求四边形ABCD的面积.17.已知圆C经过(21)A，，(50)B，两点，且圆心C在直线2yx上.（1）求圆C的方程；（2）动直线l：(2)(21)780mxmym过定点M，斜率为1的直线m过点M，直线m和圆C相交于P，Q两点，求PQ的长度.18.斜棱柱111ABCABC中，侧面11AACC面ABC，侧面11AACC为菱形，160AAC，E，F分别为11AC和AB的中点。（1）求证：平面CEF平面ABC；（2）若三棱柱的所有棱长为2，求三棱柱FECB的体积；（3）D为棱BC上一点，若1CDEF∥，请确定点D位置，并证明你的结论.19.已知圆C的圆心在直线310xy上，且圆C在x轴、y轴上截得的弦长AB和MN分别为25和42.（1）求圆C的方程；（2）若圆心C位于第四象限，点()Pxy，是圆C内一动点，且x，y满足225(1)2xy，求PAPB的范围.20.已知3(1)2A，，(02)B，，(10)C，，斜率为12的直线l过点A，且l和以C为圆C相切.（1）求圆C的方程；（2）在圆C上是否存在点P，使得22PBPA，若存在，求出所有的点P的坐标；若不存在说明理由；（3）若不过C的直线m与圆C交于M，N两点，且满足CM，MN，CN的斜率依次为等比数列，求直线m的斜率.2017-2018学年第一学期期中试卷高二数学参考答案一、填空题1.1352.1(1)2，3.平行或异面4.355.22(2)(1)5xy6.227.108.①④9.230xy10.4π311.712.18313.(13)，14.35(1][)44，，二、解答题15.证：（1）2ABCDMCMDABCMCDAB∥∥四边形ABCM为平行四边形AMBCBCPBCAMPBCAMPBC面面面∥∥（2）PCPDPMCDMCD的中为点（3）BCABAMBCCDAMCDAB∥∥PMCDAMCDCDPAMCDPAAMPMMPAPAMAMPMPAM面面，面16.解：（1）方法（一）：设()Dxy，，ABDC，(16)(23)xy，，，∴3x，9y，即(39)D，.法二：AC中点为1(4)2，，该点也为BD中点，设()Dxy，，则可得(39)D，；（2）∵，∴CD边上的高的6CDk斜率为16，∴CD边上的高所在的直线方程为：2966xy；（3）法一：BC：10xy，∴A到BC的距离为|151|5222，又42BC，∴四边形ABCD的面积为5242202.法二：∵13AC，37AB，42BC∴由余弦定理得7cos74ABC∴5sin74ABC∴四边形ABCD的面积为5sin37422074ABBCABC。17.解：（1）设圆C的方程为220xyDxEyF，则2052502DEFDFED，解得4D，8E，5F，∴圆C的方程：224850xyxy；（2）动直线l的方程为(27)280xymxy.则270280xyxy得32xy，∴动直线l过定点(32)M，，∴直线m：1yx，∴圆心(24)C，到m的距离为322，∴PQ的长为9225822.18.解:（1）1111111111111160ACCAACCCCACECACAACACCEAC正三角形菱形中△为点1111111ABCABCACACECACECAC斜三棱柱111111AACCABCECACECABCCEFABCAACCABCACECCEFECAACC面面面面面面面面面；（2）∵CEABC面，∴CE为三棱锥EBCF的高，在1RtCCE△中，可得3CE，又∵113342242BCFABCSS△△，∴113133322FECBEBCFBCFVVCES△；（3）∵1CDEF∥，∴1C，D，E，F共面，111ECACACABCECABCECABC面面面∥∥111111ECABCACDFECDFECDFABCDBCECACFABECECDF面面面中中面∥∥∥∥为点为点.19.解：（1）设圆心为()ab，，半径为r，则有222258310brarab，，，得123abr或14741294abr，圆C：22(1)(2)9xy或2217129()()4416xy；（2）∵圆心C在第四象限，∴圆C的方程为22(1)(2)9xy，∴(510)A，，(510)B，，∴22(15)(15)(1)5PAPBxyxyxy，，，∵x，y满足225(1)2xy，∴2522PAPBy（或2152(1)2x），又∵P在圆C内，满足22(1)(2)9xy且225(1)2xy∴24850yy，解得5122y，∴5[10)2PAPB，.20.解：（1）l：240xy，∵直线l和圆C相切∴设圆C的半径为r，则|14|55r，∴圆C：22(1)5xy；（2）设()Pxy，，则由228PBPA，得22771620220xyxy，又∵点P在圆C上，∴222277162022024xyxyxyx，相减得：3250xy，代入2224xyx，得2132290xx，解得1x或913x，∴点的坐标为(11)P，或919()1313P，；（3）若直P线m的斜率不存在，则MN的斜率也不存在，不合题意：设直线m：ykxb，11()Mxy，，22()Nxy，，直线m与圆22(1)5xy联立，得222(1)2(1)40kxkbxb，由2CMCNkkk，得2121211yykxx，即2121212(1)()()kxxxxkxbkxb。整理得：22212()()0kbkxxbk，∵m不过C点，∴0kb，∴上式化为12()0kxxbk.将1222(1)1kbxxk代入得：230kbkkb，即2(1)()0kkb，∵0kb，∴21k，∴直线m的斜率为1。