平行四边形的概念和性质PPT课件

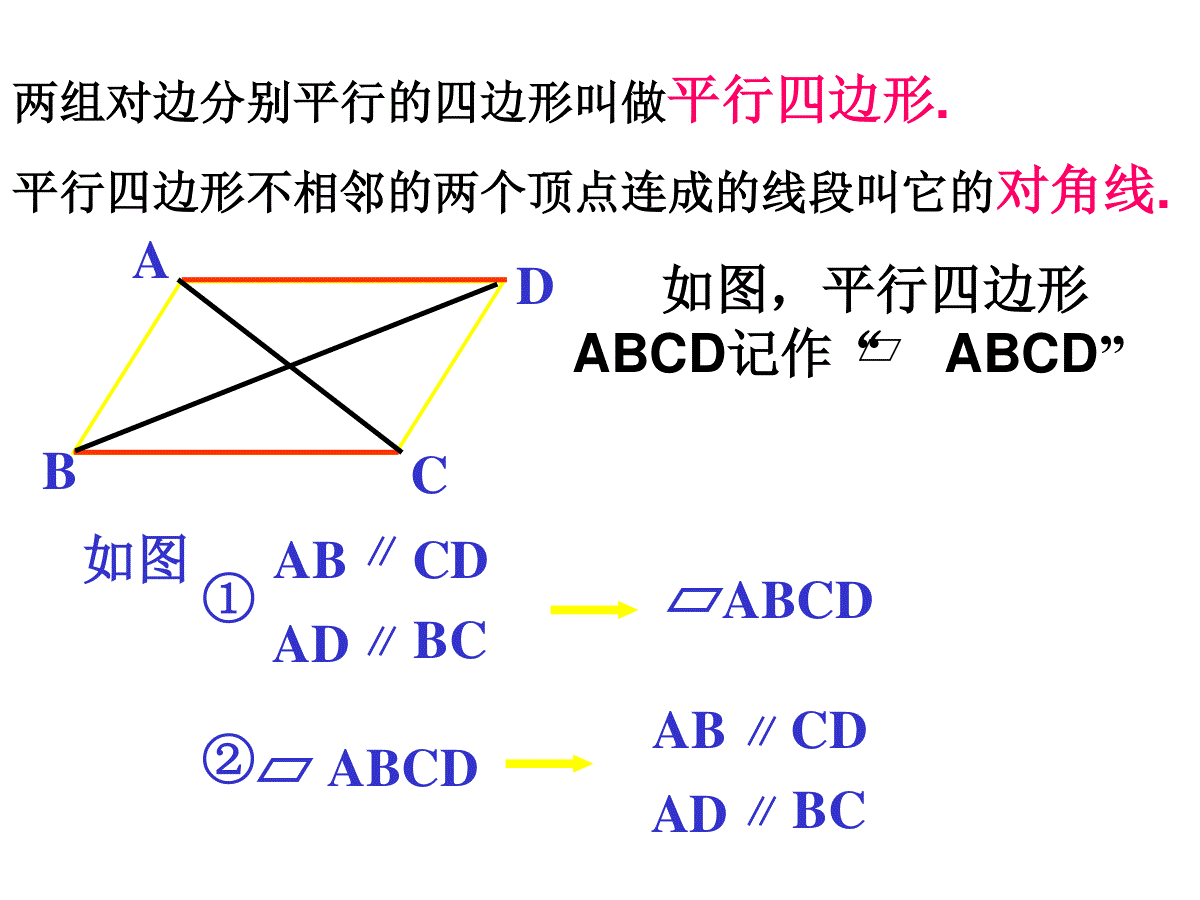
平行四边形的概念和性质(1)拉动长方形平行四边形这些都是平行四边形.ABCDADBCABCDABCD两组对边分别平行的四边形叫做平行四边形.如图，平行四边形ABCD记作“ABCD”平行四边形不相邻的两个顶点连成的线段叫它的对角线.ABCDADBC如图①ABCD②∥∥∥∥如图，DC∥EF∥AB，DA∥GH∥CB，图中的平行四边形有＿＿个，它们是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。9AHOEABCDBHGCAHGDCDEFABFECFOGDEOGBHOFDABCOHEFG做一做将平行四边形ABCD绕着对角线的交点顺时针旋转180°，然后得到的图形，与原平行四边形的位置有什么关系？平行四边形ABCD相对的边（简称对边）、相对的角（简称对角）分别有什么关系？ABCD平行四边形：两组对边分别相等两组对角分别相等验证探索自我评价标准合格：每个结论用了一种方法验证良好：每个结论用了两种方法验证优秀：每个结论用了三种或者三种以上的方法验证用什么方法验证ABCD平行四边形的性质：性质1：平行四边形的对角相等。ABCD∵四边形ABCD是平行四边形∴∠A=∠C，∠B=∠D。性质2：平行四边形的对边相等。ABCD∵四边形ABCD是平行四边形∴AB=CD，BC=AD。选择题：1、ABCD中，∠A比∠B大20°则∠C的度数为（）A、60°B、80°C、100°D、120°2、ABCD的周长为40cm，⊿ABC的周长为25cm，则对角线AC长为（）A、5cmB、15cmC、6cmD、16cmCAABCD解：∵四边形ABCD是平行四边形且∠A=32°（已知）∴∠A=∠C=32°，∠B=∠D（平行四边形的对角相等）又∵AD∥BC（平行四边形的对边平行）∴∠A+∠B=180°（两直线平行，同旁内角互补）∴∠B=∠D=180°－∠A=180º－32°=148°平行四边形中有一隐含条件：平行四边形邻角互补。例1：在ABCD中，已知∠A=32°，求其余三个角的度数。32°用两个全等的三角形纸片可以拼出几种形状不同的平行四边形？从拼图可以得到什么启示？小结：平行四边形可以看作是由两个全等的三角形组成，因此在解决平行四边形的问题时，通常可以连结对角线转化为两个全等的三角形进行解题。如图，已知平行四边形ABCD，以一组对边AD、BC向形外作等边△ADE和等边△BCF，连结BE、DF，探索BE、DF的大小关系。学会了:平行四边形的概念和一些基本性质ADCB研究对象研究结果几何表示对边邻边对角邻角对角线平行且相等相等互补∠A＝∠C，∠B＝∠DAB∥CD，AD∥BC＝＝如:∠A＋∠B＝180°O1.平行四边形的概念2.平行四边形的性质3.解决平行四边形的有关问题经常连结对角线转化为三角形。