当前位置:首页 > 电子/通信 > 综合/其它 > 6.2-坐标方法的简单应用A卷(含答案)
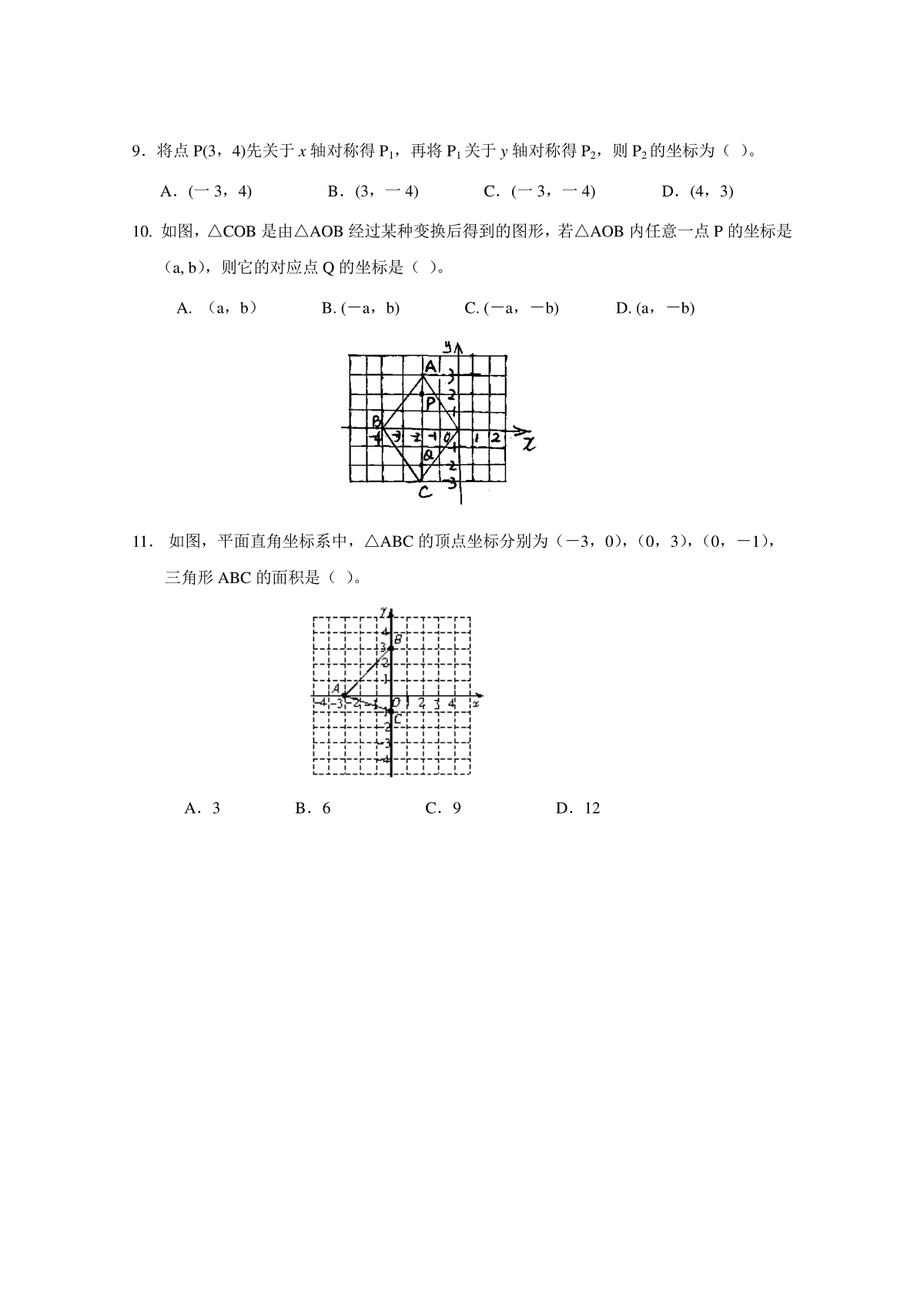
6.2坐标方法的简单应用1.将点P(2,-3)向左平移3个单位得到点P’,则点P’的坐标为()。A.(5,一3)B.(一1,一3)C.(2,0)D.(一5,一3)2.将点P(1,-m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点K(m,n)的坐标为()。A.(3,一2)B.(2,一3)C.(3,2)D.(一2,3)3.将点A(-3,5)向()平移1个单位长度,得到点A′(-3,4)。A.上B.左C.下D.右4.将△ABC的各顶点的横坐标分别加3,纵坐标不变,连接三个新的点所成的三角形是由△ABC()。A.向左移3个单位所得B.向右平移3个单位所得C.向上移3个单位所得D.向下平移3个单位所得5.已知:ABC△的顶点坐标分别为(43)A,,(03)B,,(21)C,,如将B点向右平移2个单位后再向上平移4个单位到达1B点,若设ABC△的面积为1S,1ABC△的面积为2S,则12SS,的大小关系为()。(A)12SS(B)12SS(C)12SS(D)不能确定6.平面直角坐标系中,将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比()。A.横坐标不变,纵坐标加3B.纵坐标不变,横坐标加3C.横坐标不变,纵坐标乘以3D.纵坐标不变,横坐标乘以37.线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为()。A.(2,9)B.(5,3)C.(1,2)D.(–9,–4)8.在直角坐标系中描出下列各点:A(4,1),B(1,3),C(1,-1),D(-2,1).连接AB、CD,两线段的关系为()。A.平行B.相等C.平行且相等D.相等但不平行9.将点P(3,4)先关于x轴对称得P1,再将P1关于y轴对称得P2,则P2的坐标为()。A.(一3,4)B.(3,一4)C.(一3,一4)D.(4,3)10.如图,△COB是由△AOB经过某种变换后得到的图形,若△AOB内任意一点P的坐标是(a,b),则它的对应点Q的坐标是()。A.(a,b)B.(-a,b)C.(-a,-b)D.(a,-b)11.如图,平面直角坐标系中,△ABC的顶点坐标分别为(-3,0),(0,3),(0,-1),三角形ABC的面积是()。A.3B.6C.9D.12参考答案1.将点P(2,-3)向左平移3个单位得到点P’,则点P’的坐标为()。A.(5,一3)B.(一1,一3)C.(2,0)D.(一5,一3)知识点:用坐标表示平移知识点的描述:在直角坐标系中,将点(x,y)向右平移a个单位长度,可以得到对应点(x+a,y),将点(x,y)向上平移b个单位长度,可以得到对应点(x,y+b)。在直角坐标系中,将点(x,y)向左平移a个单位长度,可以得到对应点(x-a,y),将点(x,y)向下平移b个单位长度,可以得到对应点(x,y一b)。点拨:关键是搞清平移方向。若沿x轴平移,则横坐标变化而纵坐标不变;若沿y轴平移,则纵坐标变化而横坐标不变。向着某坐标轴的正方向移动,相应的坐标增大。向着某坐标轴的负方向移动,相应的坐标减小。答案:B.详解:将点P(2,-3)向左平移3个单位得到点P’,纵坐标不变,横坐标减小了3,所以点P’的坐标为(一1,一3),选B。2.将点P(1,-m)向右平移2个单位后,再向上平移1个单位得到点Q(n,3),则点K(m,n)的坐标为()。A.(3,一2)B.(2,一3)C.(3,2)D.(一2,3)知识点:用坐标表示平移知识点的描述:在直角坐标系中,将点(x,y)向右平移a个单位长度,可以得到对应点(x+a,y),将点(x,y)向上平移b个单位长度,可以得到对应点(x,y+b)。在直角坐标系中,将点(x,y)向左平移a个单位长度,可以得到对应点(x-a,y),将点(x,y)向下平移b个单位长度,可以得到对应点(x,y一b)。点拨:关键是搞清平移方向。若沿x轴平移,则横坐标变化而纵坐标不变;若沿y轴平移,则纵坐标变化而横坐标不变。向着某坐标轴的正方向移动,相应的坐标增大。向着某坐标轴的负方向移动,相应的坐标减小。答案:D详解:将点P(1,-m)向右平移2个单位后,再向上平移1个单位,横坐标增大了2,纵坐标增大了1,得到的点Q(n,3)的坐标应为(3,-m+1),所以n=3,-m+1=3;所以n=3,m=-2;则点K(m,n)的坐标为(一2,3)。选D。3.将点A(-3,5)向()平移1个单位长度,得到点A′(-3,4)。A.上B.左C.下D.右知识点:用坐标表示平移知识点的描述:在直角坐标系中,将点(x,y)向右平移a个单位长度,可以得到对应点(x+a,y),将点(x,y)向上平移b个单位长度,可以得到对应点(x,y+b)。在直角坐标系中,将点(x,y)向左平移a个单位长度,可以得到对应点(x-a,y),将点(x,y)向下平移b个单位长度,可以得到对应点(x,y一b)。答案:C.详解:将点A(-3,5)平移后,得到点A′(-3,4),横坐标不变,纵坐标减少了1,所以只做了纵向的移动,向下平移了1个单位长度。4.将△ABC的各顶点的横坐标分别加3,纵坐标不变,连接三个新的点所成的三角形是由△ABC()。A.向左移3个单位所得B.向右平移3个单位所得C.向上移3个单位所得D.向下平移3个单位所得知识点:用坐标表示平移知识点的描述:在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度得到的图形;如果把它各个点的纵坐标都加(或减去)一个正数,相应的新图形就是把原图形向上(或向下)平移a个单位长度得到的图形。答案:B.详解:△ABC的各顶点的横坐标分别加3,纵坐标不变,相应的新图形就是把△ABC向右平移3个单位长度所成的三角形。5.已知:ABC△的顶点坐标分别为(43)A,,(03)B,,(21)C,,如将B点向右平移2个单位后再向上平移4个单位到达1B点,若设ABC△的面积为1S,1ABC△的面积为2S,则12SS,的大小关系为()。(A)12SS(B)12SS(C)12SS(D)不能确定知识点:平移的应用知识点的描述:整个图形的平移不改变图形的形状和大小,当然也不改变图形的面积。如果只移动某一个点,那么就会改变图形的形状和大小,面积的变化要具体的看点的移动情况。答案:B详解:(03)B,点向右平移2个单位后再向上平移4个单位到达1B点,其坐标为(2,1),画图可知ABC△和1ABC△同底等高,面积相同。所以选B。6.平面直角坐标系中,将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比()。A.横坐标不变,纵坐标加3B.纵坐标不变,横坐标加3C.横坐标不变,纵坐标乘以3D.纵坐标不变,横坐标乘以3知识点:用坐标表示平移知识点的描述:在平面直角坐标系内,如果把一个图形向右(或向左)平移a个单位长度,那么各个点的横坐标都加(或减去)一个正数a;如果把一个图形向上(或向下)平移a个单位长度,那么各个点的纵坐标都加(或减去)一个正数a。答案:A详解:将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比横坐标不变,纵坐标加3。7.线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为()。A.(2,9)B.(5,3)C.(1,2)D.(–9,–4)知识点:用坐标表示平移知识点的描述:一个图形经过平移后,各点的坐标都发生了完全相同的变化。答案:C详解:点A(–1,4)的对应点为C(4,7),横坐标加了5,纵坐标加了3,那么把B(–4,–1)也横坐标加5,纵坐标加3,就得到D点的坐标(1,2)。8.在直角坐标系中描出下列各点:A(4,1),B(1,3),C(1,-1),D(-2,1).连接AB、CD,两线段的关系为()。A.平行B.相等C.平行且相等D.相等但不平行知识点:用坐标表示平移知识点的描述:一个图形经过移动后,各点的坐标都发生了完全相同的变化。那么整个图形就是作了相应的平移。答案:C详解:A(4,1)到C(1,-1),B(1,3)到D(-2,1)他们的坐标的变化相同,所以线段CD就是线段AB平移得到的对应线段。根据平移的性质,对应的线段是平行且相等的。详解:将△ABC的各点的横坐标都加3,纵坐标不变,各点的坐标的变化相同,所以△ABC只是作了向右三个单位的平移,△ABC的形状和大小不变。选B。9.将点P(3,4)先关于x轴对称得P1,再将P1关于y轴对称得P2,则P2的坐标为()。A.(一3,4)B.(3,一4)C.(一3,一4)D.(4,3)知识点:用坐标表示对称知识点的描述:P(x,y)关于x轴的对称点为(x,-y);P(x,y)关于y轴的对称点为(-x,y);P(x,y)关于原点的对称点为(-x,-y)。答案:C详解:P(3,4)先关于x轴对称得P1(3,-4),P1(3,-4)关于y轴对称得P2(-3,-4)。所以选C。10.如图,△COB是由△AOB经过某种变换后得到的图形,若△AOB内任意一点P的坐标是(a,b),则它的对应点Q的坐标是()。A.(a,b)B.(-a,b)C.(-a,-b)D.(a,-b)知识点:用坐标表示对称知识点的描述:P(x,y)关于x轴的对称点为(x,-y);P(x,y)关于y轴的对称点为(-x,y);P(x,y)关于原点的对称点为(-x,-y)。答案:D详解:△AOB与△COB关于x轴对称,点P(a,b)关于x轴的对称点为(a,-b),则它的对应点Q的坐标是(a,-b)。11.如图,平面直角坐标系中,△ABC的顶点坐标分别为(-3,0),(0,3),(0,-1),三角形ABC的面积是()。A.3B.6C.9D.12知识点:求坐标系中的图形的面积知识点的描述:通过观察坐标找出有关线段的长度,进而求出有关图形的面积。答案:B详解:根据三个顶点的坐标特征可以看出,△ABC的边BC在y轴上,由图形可得BC=4,点A到BC边的距离就是A点到y轴的距离,也就是A点横坐标的绝对值,所以三角形ABC的面积为S△ABC=BC×AO=×4×3=6。




 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:6.2-坐标方法的简单应用A卷(含答案)
链接地址:https://www.777doc.com/doc-4905097 .html