当前位置:首页 > 商业/管理/HR > 信息化管理 > 第十四章 结构的稳定计算
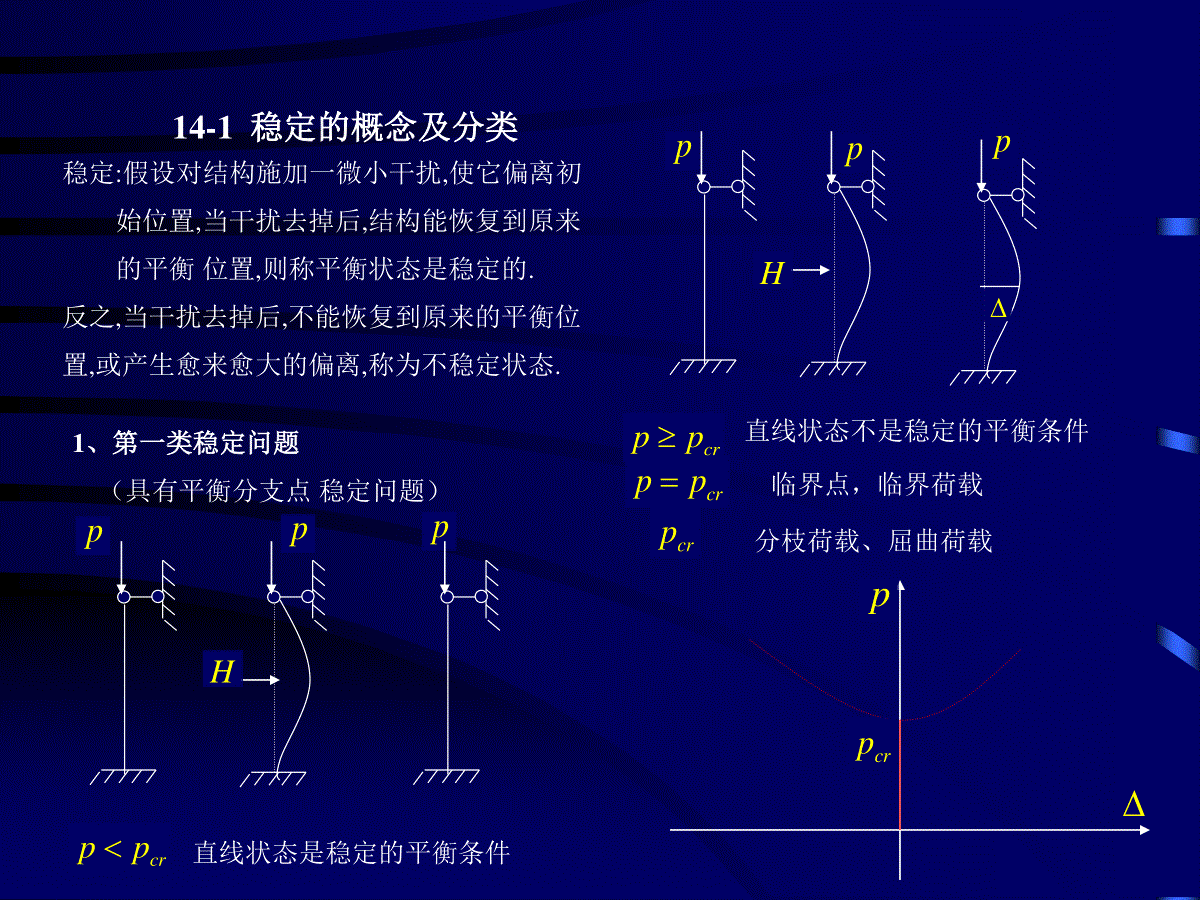
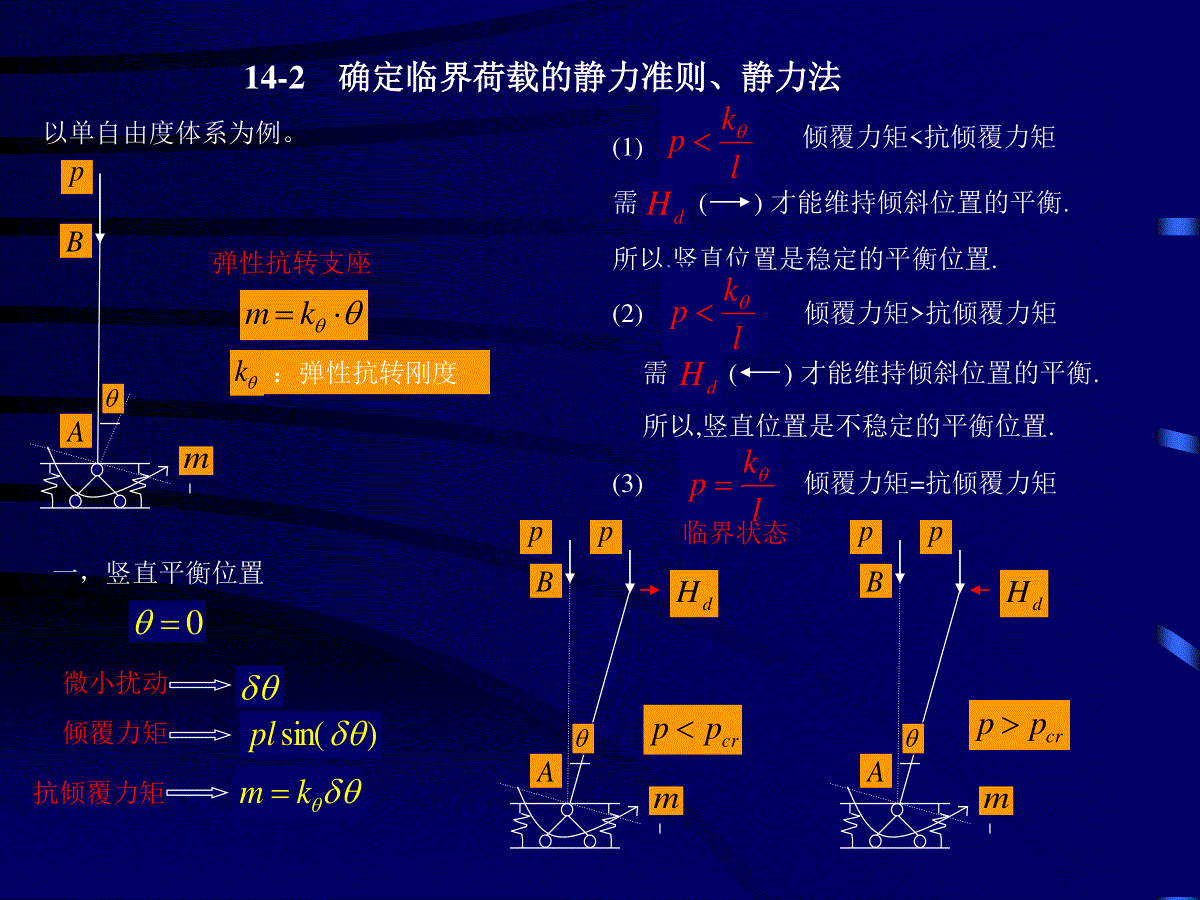
结构力学课件(下册)•建筑工程学院第十四章结构的稳定计算14-1稳定的概念及分类14-2确定临界荷载的静力准则,静力法14-3初参数法求临界荷载14-4确定临界荷载的能量准则,能量法14-1稳定的概念及分类稳定:假设对结构施加一微小干扰,使它偏离初始位置,当干扰去掉后,结构能恢复到原来的平衡位置,则称平衡状态是稳定的.反之,当干扰去掉后,不能恢复到原来的平衡位置,或产生愈来愈大的偏离,称为不稳定状态.1、第一类稳定问题(具有平衡分支点稳定问题)pppcrpp直线状态是稳定的平衡条件pppHHcrpp直线状态不是稳定的平衡条件crpp临界点,临界荷载crp分枝荷载、屈曲荷载pcrp第一类稳定问题:当荷载达到临界荷载时(),平衡形式发生了质的变化。(由直线变为曲线)即出现了新的平衡形式。crpp实际上,屈曲后,荷载虽可稍作增加,变形迅速增大,所以是可承担荷载的最大值。crppcrpp梁在原平面内弯曲(平衡理论)crpp梁偏离原平面发生弯曲和扭转(新的平衡理论)pp①Hpp②pp③ppH①pp②crppcrpp14-2确定临界荷载的静力准则、静力法以单自由度体系为例。pBAmkm弹性抗转支座k:弹性抗转刚度dHpBAmp一,竖直平衡位置0微小扰动倾覆力矩)sin(pl抗倾覆力矩km(1)lkp倾覆力矩抗倾覆力矩需()才能维持倾斜位置的平衡.dH所以,竖直位置是稳定的平衡位置.lkp(2)倾覆力矩抗倾覆力矩需()才能维持倾斜位置的平衡.dH所以,竖直位置是不稳定的平衡位置.lkp(3)倾覆力矩=抗倾覆力矩临界状态dHpBAmpcrppcrpp第二类稳定问题,例:偏心受压的直杆pecrpp特点:当荷载达到临界荷载时()结构变形大大发展,但不会出现新的变形形式。即:平衡形式不出现质变。crpp第二类稳定问题涉及到大变形和塑性问题。本章只考虑第一类稳定问题。注意:稳定问题与强度问题的区别。(1)稳定问题:求,使结构变形形式发生质变的最小荷载值。强度问题:求,使结构内力取最大的荷载值。crpup(2)稳定问题:需在变形后的形状上建立平衡方程。强度问题:在变形前的形状上建立平衡方程。(3)稳定问题:研究的目的是防止出现不稳定的平衡状态。强度问题:研究的目的是防止机构达到极限状态。二、倾斜平衡位置0kmplsinsinlkp三、按大挠度分析2sin)cos(sinlkddp00ddp00ddplkp0pP--曲线在处出现分枝,crp2、按小挠度分析sinlkpsinlkp当荷载达到时,杆件处于随遇状态。crp小挠度pcrp大挠度分析:(1)两种理论(小挠度与大挠度)得到的临界荷载是一样的。lkpcr(2)crpp所以,竖直位置是稳定的平衡位置.crpp所以,竖直位置是不稳定的平衡位置.(3)按大挠度理论屈曲后,P--是一条曲线,但此曲线非常接近直线。按小挠度理论屈曲后,P--是一条直线。(4)不需研究屈曲后状态时,可采用小挠度理论。(5)对于小挠度理论,当荷载时,平衡状态出现随遇性。crpp静力准则:当荷载达到临界荷载时,平衡状态出现随遇性,除了原来的竖向平衡状态外,还存在着其它的平衡状态。静力法:采用静力准则求临界荷载的方法叫静力法。例:一中心受压的直杆,一边固支,一边链接支承。求:crppABlEIcrpxy解:当P达到时,开始出现弯曲的平衡位置.crp)(xlRyPM''EIyMEIp令)(2''xlEIpyy通解为)(sincosxlPRxBxAyPRBA、、待定边际条件000’、、yyx0ylx、0sincos00lBlAPRBlPRA非零解00sincos1001lllDlltg稳定方程图解法求解稳定方程.493.4)(minl222min)7.0()(lEIEIPcr弹性直线荷载的统一表达式22)(lEIPcr注意:最终只能得到的比值,得不出具体的值,因此,实际上最终得到的是挠曲线的形状,而不是具体的挠曲线.PRBA、、用静力法求临界荷载的步骤:(1)在微弯状态下列平衡方程,(挠度y的微分方程)(2)代入边界条件,得一组线形代数方程.(3)由方程组的系数行列式D=0,得到crp例:BC段是刚体,建立稳定方程.pCBAEIllxxcrPyyBcrpp解:当时,出现了新的平衡状态,弯曲平衡状态。)(ypM''EIyMEIp令22''yy通解为:xxAysincos边条:000’、、yyxlyylxlxB)('、0)sincos()cossin(00lllBlllABA00sincoscossin010101llllllDlltg1稳定方程稳定方程:14-3初参数法求临界荷载本节要推导出高阶的,普遍适用于各种支承情况的微分方程,并导出压杆挠曲后位移及内力的初参数表达式.pp0MpHpH0Mdx0sin)(cos)(,0ddNNQddQQt取微分段.水平力H,竖向力PsincosHPN0sin)(cos)(,0ddQQNddNNn0,0QdxMdMMMdNNNQMdQQdMMnt小变形ddsin,1cos,1cos,sinH,Q,是次要内力,N是主要内力.QdxdMdNNddQPN00dxdPdxMd22'''.ydxdyEIyM0''2)4(yy高阶微分方程,适用于一切边际条件.通解:4321sincosCxCxCxCy00'00,,,QMyy代入4个初参数得:200420'03302201,,,EIMyCEIQyCEIQCEIMC初参数方程:(用初参数表示的位移及内力.)sincossincos)cos1(sin)sin()cos1(0000200'0'3020'00xMxQQxQxMMxEIQxEIMyyxxEIQEIMyyy例:中心受压直杆,一端固支,一端有支坐链杆。解:边界条件000’、、yyx00llMylx、、两个初参数为0,另两个未知。0sincos0)sin()cos1(0000lQlMQllMl系数行列式值为00sincossin)cos1(lllll稳定方程lltg00llMy因为当荷载P达到时,出现了新的平衡方式。(除了直杆外,还有新的平衡方式)crp所以,与不能同时为00M0Q例,求临界荷载。lp1I2IEACBA323lEIk将原结构简化为一受压直杆。一端固支,一端弹性支撑。pK1IAB边界条件:00000’、、yyxllllkyypQMlx'0、、两个初参数为0,另两个未知,但不应该同时为00)sin()cos1(0sincos0313102100QkEIllEIkMlEIkQllM由0D0)sin()cos1(sincos313121kEIllEIklEIkll稳定方程kEIlltg31几种特殊情况。0,0)12kI2)(,minlltglplkyABly1IllllkypyQM'0是竖柱的临界荷载22)2(lEIpcrkI,)22493.4)(minllltg一端固支,一端链杆支承493.4~2:)(minl当31123,lEIkII稳定方程3)(3llltg试算法求解:取518.1,0.2yl例:列稳定方程。pBAAB解:原结构简化为一根中心受压直杆,一端是链杆支座,一端是弹性抗转支座。lEIk6边界条件:00000Myx、、(B端)'0lllykMylx、、两个初参数为0,另两个未知0D稳定方程6)(112llltg3)在0间2I~设)3)((3llltgy192.1,4.2yl在2.0~2.4之间。l042.0,2.2yl2.2)(minl222)43.1(lEIEIpcr14-4能量法一、能量准则以单自由度体系为例crpp)1rrrTTTcrpp)2直杆处于随遇平衡状态rT定义:保守力系:外力做功只与力作用点初始和最终位置有关。rTw外力势能rTw体系总势能0:crpp0:crpp能量准则:0体系处于临界状态()crpppAppApdH加维持倾斜平衡状态dH:P做功rT:做功rTdH0rT:变形能例:14-6.用能量法求crp221)cos1(lle221lpePTr221k0rTlkpcr例:求临界荷载crp只考虑弯曲变形能pApedxpexydxdxldxEIM0221ldxyEI02'')(21epTrdxypTlr02')(20rTllcrdxydxyEIp02'02'')()(注:(1)若已知挠曲线,则可得精确解.若不知挠曲线,需假设挠曲线,可得近似解.)(xyy(3)计算得出的近似解精确解(4)可取杆件在某一横向荷载下的挠曲线作为近似曲线.dxydxde2')(21)cos1('y(2)假设的挠曲线,应满足变形协调条件(位移边条及连续条件))(xyy例:14-7.用能量法计算crpp解:1、设挠曲线为水平力H作用下的挠曲线lxHldxy0232)(''3)()2(2')(xlxHyx)62(32xlxHycxyx2)('225lEIpcr22)2(lEI精确解:误差为:1.4%2cxy2、设挠曲线为23lEIpcr误差为:21.3%分析:(1)设定的挠曲线均能满足位移边条和连续条件,但前者尚能满足自由端弯矩为0的条件,后者却不能。(2)设定挠曲线时应注意:位移边条一定满足:弯矩条件尽量满足。px)('')(xlHyxlxHldxy0252)('152)(cyx2)(''二,用最小势能原理求crp最小总势能原理:在所有可能的挠曲线中,真实的挠曲线使体系的总势能取最小值。)()(22)(11)(xnnxxxaaay),(21naaa),.....2,1(,001''01''''nidxapdxalnjijjlnjijj),2,1(,0niai设:驻值条件:njjijijaPRA10)(ljiijdxEIA0''''几个线性齐次方程。nnnnnnnnnnnnPRAPRAPRAPRAPRAPRAPRAPRAPRAD..........................................221122222221211112121111展开可得稳定方程。wlldxypdxyEI02'02'')(2)(21ljiijdxR0''不全为0。naaa.......,21例:14-8求压杆的临界荷载。EI=常数设:满足位移边条及连续条件。)(22)(11)(xxxaay)()(3)(22)(1xlxxlxxx2')(132xlxxxlx62'')(132')(243xlxx2'



 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:第十四章 结构的稳定计算
链接地址:https://www.777doc.com/doc-5090873 .html