三角学的起源与发展

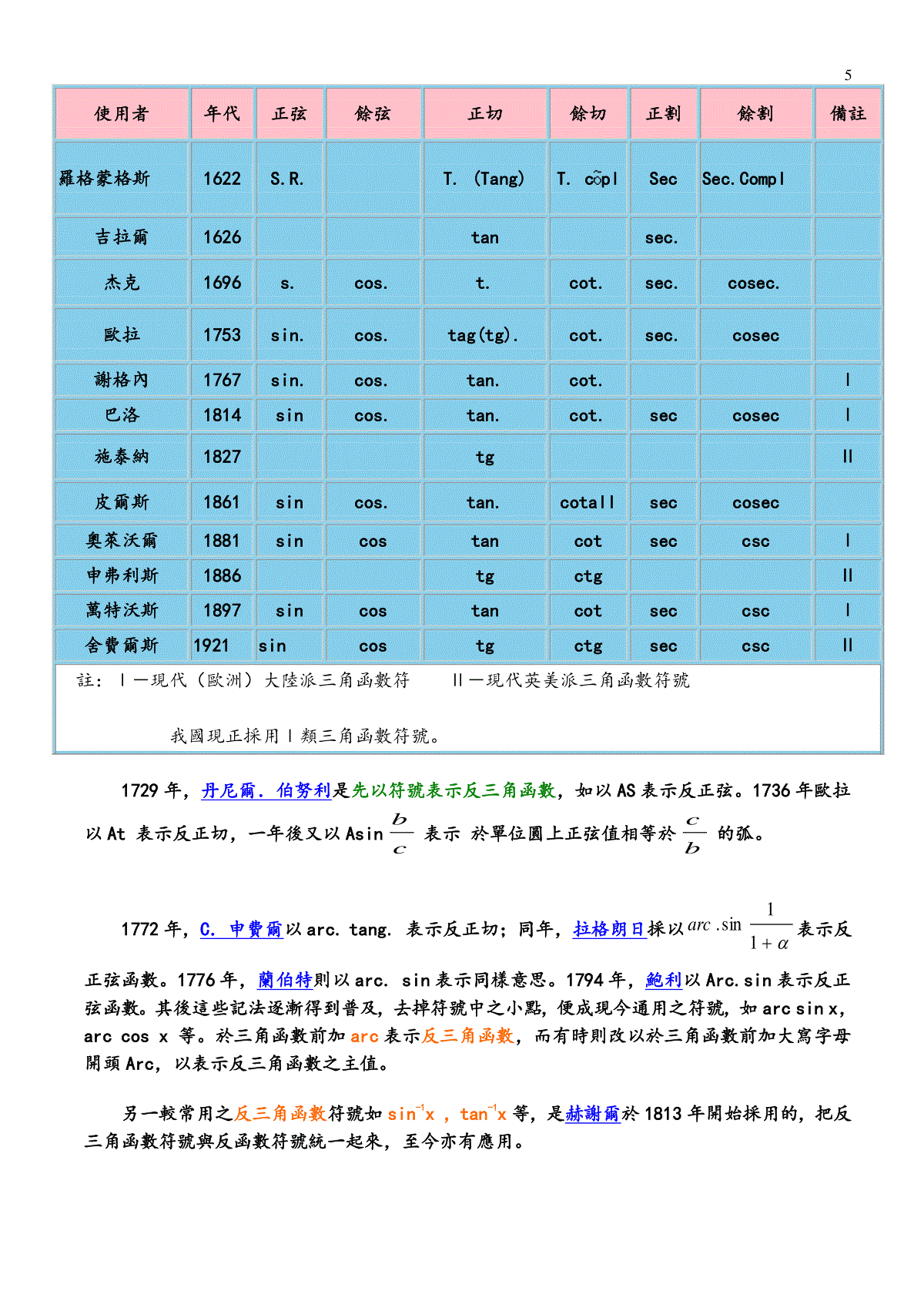
1壹、三角學的起源與發展三角學之英文名稱Trigonometry，約定名於西元1600年，實際導源於希臘文trigono(三角)和metrein(測量)，其原義為三角形測量（解法），以研究平面三角形和球面三角形的邊和角的關係為基礎，達到測量上的應用為目的的一門學科。早期的三角學是天文學的一部份，後來研究範圍逐漸擴大，變成以三角函數為主要對象的學科。現在，三角學的研究範圍已不僅限於三角形，且為數理分析之基礎，研究實用科學所必需之工具。(一)西方的發展三角學﹝Trigonometry﹞創始於西元前約150年，早在公元前300年，古代埃及人已有了一定的三角學知識，主要用於測量。例如建築金字塔、整理尼羅河泛濫後的耕地、通商航海和觀測天象等。公元前600年左右古希臘學者泰勒斯(p13)利用相似三角形的原理測出金字塔的高，成為西方三角測量的肇始。公元前2世紀後希臘天文學家希帕霍斯（HipparchusofNicaea）為了天文觀測的需要，作了一個和現在三角函數表相仿的「弦表」，即在固定的圓內，不同圓心角所對弦長的表，他成為西方三角學的最早奠基者，這個成就使他贏得了「三角學之父」的稱謂。公元2世紀，希臘天文學家數學家托勒密(Ptolemy)(85-165)繼承希帕霍斯的成就，加以整理發揮，著成《天文學大成》13卷，包括從0°到90°每隔半度的弦表及若干等價於三角函數性質的關係式，被認為是西方第一本系統論述三角學理論的著作。約同時代的梅內勞斯（Menelaus）寫了一本專門論述球三角學的著作《球面學》，內2容包球面三角形的基本概念和許多平面三角形定理在球面上的推廣，以及球面三角形許多獨特性質。他的工作使希臘三角學達到全盛時期。(二)中國的發展我國古代沒有出現角的函數概念，只用勾股定理解決了一些三角學範圍內的實際問題。據《周髀算經》記載，約與泰勒斯同時代的陳子已利用勾股定理測量太陽的高度，其方法後來稱為「重差術」。1631西方三角學首次輸入，以德國傳教士鄧玉函、湯若望和我國學者徐光啟(p20)合編的《大測》為代表。同年徐光啟等人還編寫了《測量全義》，其中有平面三角和球面三角的論述。1653年薛風祚與波蘭傳教士穆尼閣合編《三角算法》，以「三角」取代「大測」，確立了「三角」名稱。1877年華蘅煦等人對三角級數展開式等問題有過獨立的探討。現代的三角學主要研究角的特殊函數及其在科學技術中的應用，如幾何計算等，多發展於20世紀中。貳、三角函數的演進正弦函數、餘弦函數、正切函數、餘切函數、正割函數、餘割函數統稱為三角函數（Trigonometricfunction）。儘管三角知識起源於遠古，但是用線段的比來定義三角函數，是歐拉(p16)（1707-1783）在《無窮小分析引論》一書中首次給出的。在歐拉之前，研究三角函數大都在一個確定半徑的圓內進行的。如古希臘的托勒密定半徑為60；印度人阿耶波多（約476-550）定半徑為3438；德國數學家里基奧蒙特納斯（1436-1476）為了精密地計算三角函數值曾定半徑600,000；後來為製訂更精密的正弦表又定半徑為107。因此，當時的三角函數實際上是定圓內的一些線段的長。意大利數學家利提克斯（1514-1574）改變了前人的做法，即過去一般稱AB為的正弦，把正弦與圓牢牢地連結在一起（如下頁圖），而利提克斯卻把它稱為∠AOB的正弦，從而使正弦值直接與角掛勾，而使圓O成為從屬地位了。到歐拉(Euler)時，才令圓的半徑為1，即置角於單位圓之中，從而使三角函數定義為相應的線段與圓半徑之比。1.正弦、餘弦DCB0AP3在△ABC中，a、b、c為角A、B、C的對邊，R為△ABC的外接圓半徑，則有稱此定理為正弦定理。正弦定理是由伊朗著名的天文學家阿布爾.威發(940-998)首先發現與証明的。中亞細亞人阿爾比魯尼﹝973-1048﹞(p15)給三角形的正弦定理作出了一個証明。也有說正弦定理的証明是13世紀的那希爾丁在《論完全四邊形》中第一次把三角學作為獨立的學科進行論述，首次清楚地論証了正弦定理。他還指出，由球面三角形的三個角，可以求得它的三個邊，或由三邊去求三個角。這是區別球面三角與平面三角的重要標誌。至此三角學開始脫離天文學，走上獨立發展的道路。托勒密（ClaudiusPtolemy）的《天文學大成》第一卷除了一些初級的天文學資料之外，還包括了上面講的弦表：它給出一個圓從（21）°到180°每隔半度的所有圓心角所對的弦的長度。圓的半徑被分為60等分，弦長以每一等分為單位，以六十進位制表達。這樣，以符號crda表示圓心角ａ所對的弦長，例如crd36°=37p4'55，意思是：36°圓心角的弦等於半徑的6037（或37個小部分），加上一個小部分的604，再加上一個小部分的360055，從下圖看出，弦表等價於正弦函數表，因為1202OsincrdABOAAB的直徑圓公元6世紀初，印度數學家阿耶波多製作了一個第一象限內間隔3°45'的正弦表，依照巴比倫人和希臘人的習慣，將圓周分為360度，每度為60分，整個圓周為21600份，然後據2πr=216000，得出r=3438﹝近似值﹞，然後用勾股定理先算出30°、45°、90°的正弦之後，再用半角公式算出較小角的正弦值，從而獲得每隔3°45'的正弦長表；其中用同一單位度量半徑和圓周，孕育著最早的弧度制概念。他在計算正弦值的時候，取圓心角所對弧的半弦長，比起希臘人取全弦長更近於現代正弦概念。印度人還用到正矢和餘弦，並給出一些三角函數的近似分數式。AMααααBAO42.正切、餘切著名的敘利亞天文學、數學家阿爾一巴坦尼﹝850-929﹞於920年左右，製成了自0°到90°相隔1°的餘切[cotangent]表。公元727年，僧一行受唐玄宗之命撰成《大行曆》。為了求得全國任何一地方一年中各節氣的日影長度，一行編出了太陽天頂距和八尺之竿的日影長度對應表，而太陽天頂距和日影長度的關係即為正切﹝tangent﹞函數。而巴坦尼編製的是餘切函數表，而太陽高度﹝角﹞和太陽天頂距﹝角﹞互為餘角，這樣兩人的發現實際上是一回事，但巴坦尼比一行要晚近200年。14世紀中葉，中亞細亞的阿魯伯﹝1393-1449﹞，原是成吉思汗的後裔，他組織了大規模的天文觀測和數學用表的計算。他的正弦表精確到小數9位。他還製造了30°到45°之間相隔為1'，45°到90°的相隔為5'的正切表。在歐洲，英國數學家、坎特伯雷大主教布拉瓦丁﹝1290？-1349﹞首先把正切、餘切引入他的三角計算之中。3.正割、餘割正割﹝secant﹞及餘割﹝cosecant﹞這兩個概念由阿布爾─威發首先引入。sec這個略號是1626年荷蘭數基拉德﹝1595-1630﹞在他的《三角學》中首先使用，後經歐拉採用才得以通行。正割、餘割函數的現代定義亦是由歐拉給出的。歐洲的「文藝復興時期」，﹝14世紀-16世紀﹞偉大的天文學家哥白尼﹝1473-1543﹞提倡地動學說，他的學生利提克斯見到當時天文觀測日益精密，認為推算更精確的三角函數值表刻不容緩。於是他定圓的半徑為1015，以製作每隔10的正弦、正切及正割值表。當時還沒有對數，更沒有計算機。全靠筆算，任務十分繁重。利提克斯和他的助手們以堅毅不拔的意志，勤奮工作達12年之久，遺憾的是，他生前沒能完成這項工作，直到1596年，才由他的學生鄂圖﹝1550-1605﹞完成並公佈於世，1613年海得堡的彼提克斯﹝1561-1613﹞又修訂了利提克斯的三角函數表，重新再版。後來英國數學家納皮爾發現了對數，這就大大地簡化了三角計算，為進一步造出更精確的三角函數表創造了條件。4.三角函數符號毛羅利科早於1558年已採用三角函數符號，但當時並無函數概念，於是只稱作三角線（trigonometriclines）。他以sinus1marcus表示正弦，以sinus2marcus表示餘弦。而首個真正使用簡化符號表示三角線的人是T.芬克。他於1583年創立以“tangent”（正切）及“secant”（正割）表示相應之概念，其後他分別以符號“sin.”,“tan.”,“sec.”,“sin.com”,“tan.com”,“sec.com”表示正弦，正切，正割，餘弦，餘切，餘割，首三個符號與現代之符號相同。後來的符號多有變化，下列的表便顯示了它們之發展變化。5使用者年代正弦餘弦正切餘切正割餘割備註羅格蒙格斯1622S.R.T.(Tang)T.cplSecSec.Compl吉拉爾1626tansec.杰克1696s.cos.t.cot.sec.cosec.歐拉1753sin.cos.tag(tg).cot.sec.cosec謝格內1767sin.cos.tan.cot.Ⅰ巴洛1814sincos.tan.cot.seccosecⅠ施泰納1827tgⅡ皮爾斯1861sincos.tan.cotallseccosec奧萊沃爾1881sincostancotseccscⅠ申弗利斯1886tgctgⅡ萬特沃斯1897sincostancotseccscⅠ舍費爾斯1921sincostgctgseccscⅡ註：Ⅰ－現代（歐洲）大陸派三角函數符Ⅱ－現代英美派三角函數符號我國現正採用Ⅰ類三角函數符號。1729年，丹尼爾．伯努利是先以符號表示反三角函數，如以AS表示反正弦。1736年歐拉以At表示反正切，一年後又以Asincb表示於單位圓上正弦值相等於bc的弧。1772年，C．申費爾以arc.tang.表示反正切；同年，拉格朗日採以11sin.arc表示反正弦函數。1776年，蘭伯特則以arc.sin表示同樣意思。1794年，鮑利以Arc.sin表示反正弦函數。其後這些記法逐漸得到普及，去掉符號中之小點，便成現今通用之符號，如arcsinx，arccosx等。於三角函數前加arc表示反三角函數，而有時則改以於三角函數前加大寫字母開頭Arc，以表示反三角函數之主值。另一較常用之反三角函數符號如sin-1x，tan-1x等，是赫謝爾於1813年開始採用的，把反三角函數符號與反函數符號統一起來，至今亦有應用。6參、三角函數的和差化積公式下列公式稱為三角函數的和差化積公式。法國著名數學家韋達﹝1540-1603﹞(p18)在他的著名的三角學著作《標準數學》中收集並整理了有關三角公式並給予補充，其中就有他給出的恒等式:【後記】三角函數名稱的由來和補充想知道為何三角函數要叫做sin，cos這些名字嗎？經過了多方的查取資料，找到了下圖：上面這個圖稱為三角圓（半徑＝1），是用圖形的方式表達各函數。其中我們可以看到，sinθ為PM線段，也就是圓中一條弦（對2θ圓周角）的一半，所以稱為「正弦」。而cosθ是OM線段，但OM＝NP，故我們也可以將cosθ視為NOP（90°-θ）的正弦值，也就是θ的餘角的7正弦值，故稱之為「餘弦」。其餘類推。另外，除了課本中教的六種三角函數外，我們還查到了其他的三角函數，如上圖中的versθ、coversθ和exsecθ。事實上，在歷史上曾出現過的三角函數種類超過十種呢！但最後只剩下這六種常用的。其他的還有如半正矢（havθ）、古德曼函數和反古德曼函數等。【補充：小歷史】大部分的三角函數一開始都是由於天文上的需要而造出來的。在三角函數傳入中國時，正、餘矢函數還未廢棄，故徐光啟將八種三角函數稱為「八線」。後來因為矢類函數廢棄不用，故八線之名漸被「三角」取代，但統一的名稱還是到了民國以後才確立的。參考資料：1.梁宗巨（1995），《數學歷史典故》(九章出版社)2.王懷權《幾何發展史》(凡異出版社)參考網站：1.://home.educities.edu.tw/sanchiang/3.://dir.yahoo.com/Science/Mathematics/History/泰勒斯﹝TalesofMiletus﹞約公元前625-前54