当前位置:首页 > 商业/管理/HR > 管理学资料 > 正弦定理余弦定理复习题精讲
已知条件定理选用一般解法一边和和二角(如a,B,C)正弦定理由A+B+C=180°求角A,由正弦定理求出b与c两边和夹角(如a,b,C)余弦定理由余弦定理求出第三边c,由正弦定理求出小边所对的角,再由A+B+C=180°求出另一角.两边和其中一边的对角(如a,b,A)正弦定理由正弦定理求出角B,再求角C,最后求出c边.可有两解,一解或无解.三边(a,b,c)余弦定理由余弦定理求出角A,B,再利用A+B+C=180°求出角C.2sin2cossinsinsinsinsinsinsinsinsin,sinsinsinCBACBACBACkBkAkcbakCcBbAa原命题等价于:2sin2cos)sinsinsin(222CBACBA即可证此时右边=cBABABAAABABABABABABABABABABABABABABABACBA2222222222222sinsinsincoscossinsin2cossin)(sinsinsincoscossinsin21)(cos1)cos()cos()cos()cos(1)]cos(1)][cos(1[)]cos(1)][cos(1[)cos(1)cos(12cos12)cos(1左边。CBACBAABCABABABACBAABABA22222222222222222sin)sin(sinsinsinsin2sinsinsinsinsinsin2sinsinsincossinsinsinsinsinsin2)cos1(cos∴原等式成立.2sin2cosCBAcba2cos2sin2cos2sin2sin2sin2cos2sin2sin)22cos(2cos2sin22sin2cos2sinsinsinCBACCBACCCBACCCBABACBAcba1.有分别满足下列条件的两个三角形:(1)B=30°,a=14,b=7;(2)那么下面判断正确的是()9,10,600baBA.(1)只有一解,(2)只有一解B.(1)有两解,(2)有两解C.(1)有两解,(2)只有一解D.(1)只有一解,(2)有两解CcBbAacoscoscos2.在△ABC中,若,则△ABC是()A.等腰直角三角形B.顶角为120°的等腰三角形C.等边三角形D.以上结论均不正确3.在△ABC中,sinA:sinB:sinC=3:2:4,则cosC的值为()A.-1/4B.1/4C.-2/3D.2/34.已知锐角三角形的边长分别为2,3,x,则x的取值范围是()A.B.C.D.)5,0()5,1()13,5()15,13(5.在△ABC中,sinA=1/3,cosB=,a=1,则b等于()33A.B.C.D.33233666.在△ABC中,若b=,a=2,且这个三角形有解,则A的取值范围是()A.B.C.D.)90,0(]45,0(]30,0()60,30(228.已知△ABC的三内角的正弦之比为4:5:6,周长为7.5,则其三边长为____________.7.若A,B,C是△ABC的三个内角,则sinA+sinB____sinC(用””,””填空).CBA222sinsinsin9.在△ABC中,若,则△ABC的形状是_________三角形10.在ABC中,化简BcCbcoscos=1.如图,在四边形ABCD中,已知ADCD,AD=10,AB=14,BDA=60,BCD=135求BC的长DCBA解:在△ABD中,设BD=x则BDAADBDADBDBAcos2222即60cos1021014222xx整理得:096102xx解之:161x62x(舍去)由正弦定理:BCDBDCDBBCsinsin2830sin135sin16BC2.△ABC中,若已知三边为连续正整数,最大角为钝角,解此三角形.解:设三边1,,1kckbka,Nk且1k∵C为钝角∴0)1(242cos222kkaccbaC解得41kNk∵∴或3,但2k2k时不能构成三角形应舍去当3k时109,41cos,4,3,2CCcba在ABC中,如果,2lgsinlglglgBca且B为锐角,试判断此三角形的形状.分析:由,2lgsinlglglgBca得,22sin,22Bca即45,sinsinsinBBCA..sincossinsin)sin(CBCBCB.sincoscossinsincosCBCBCB.0cossinCB.0cosC即90C,故ABC为等腰直角三角形.在⊿ABC中,B=60°,那么a²-ac+c²-b²=______.若把一个直角三角形的三边增加同样的长度,则这个新的三角形为_______三角形。已知锐角三角形的边长分别为2,3,x,则x的取值范围是()A.B.C.D.)5,0()5,1()13,5()15,13(在⊿ABC中,如果(a+b+c)(b+c-a)=3bc,那么A等于()A.30°B.60°C.120°D.150°已知⊿ABC中,∠A=60°,最大边和最小边的长是方程3x²-27x+32=0的两实根,那么BC边长等于______.已知⊿ABC中,A=120°,b=3,c=5,则sinB+sinC=______.在△ABC中,sinA:sinB:sinC=3:2:4,则cosC的值为()A.-1/4B.1/4C.-2/3D.2/3在⊿ABC中,已知a=2,则bcosC+ccosB等于______.在△ABC中,若,则△ABC的形状是_________三角形如图,在四边形ABCD中,已知ADCD,AD=10,AB=14,BDA=60,BCD=135求BC的长DCBA解:在△ABD中,设BD=x则即整理得:由正弦定理:已知⊿ABC中,三个内角A,B,C的对边分别是a,b,c,若⊿ABC的面积为S,且2S=(a+b)²-c²,求tanC的值。在⊿ABC中,如果(a+b+c)(b+c-a)=3bc,且sinA=2sinBcosC,试确定⊿ABC的形状。


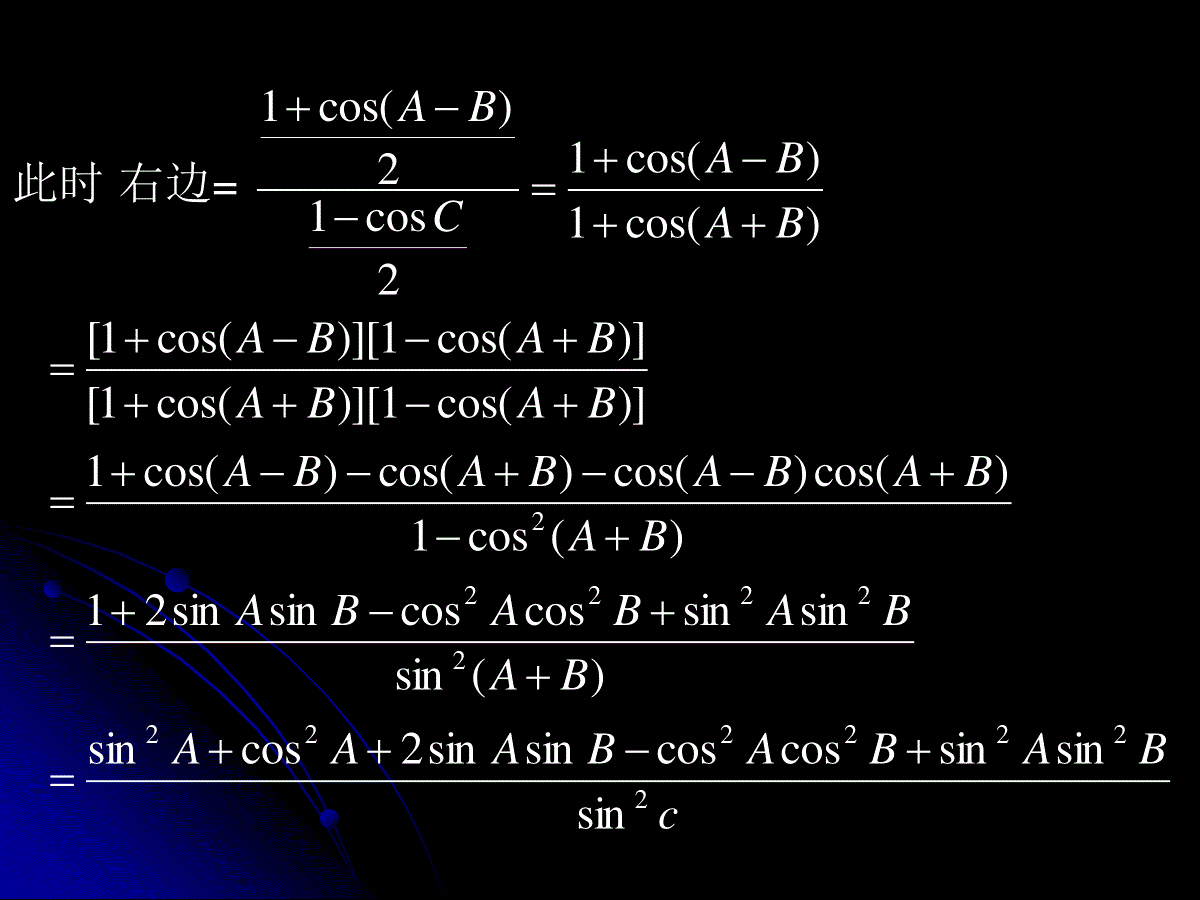
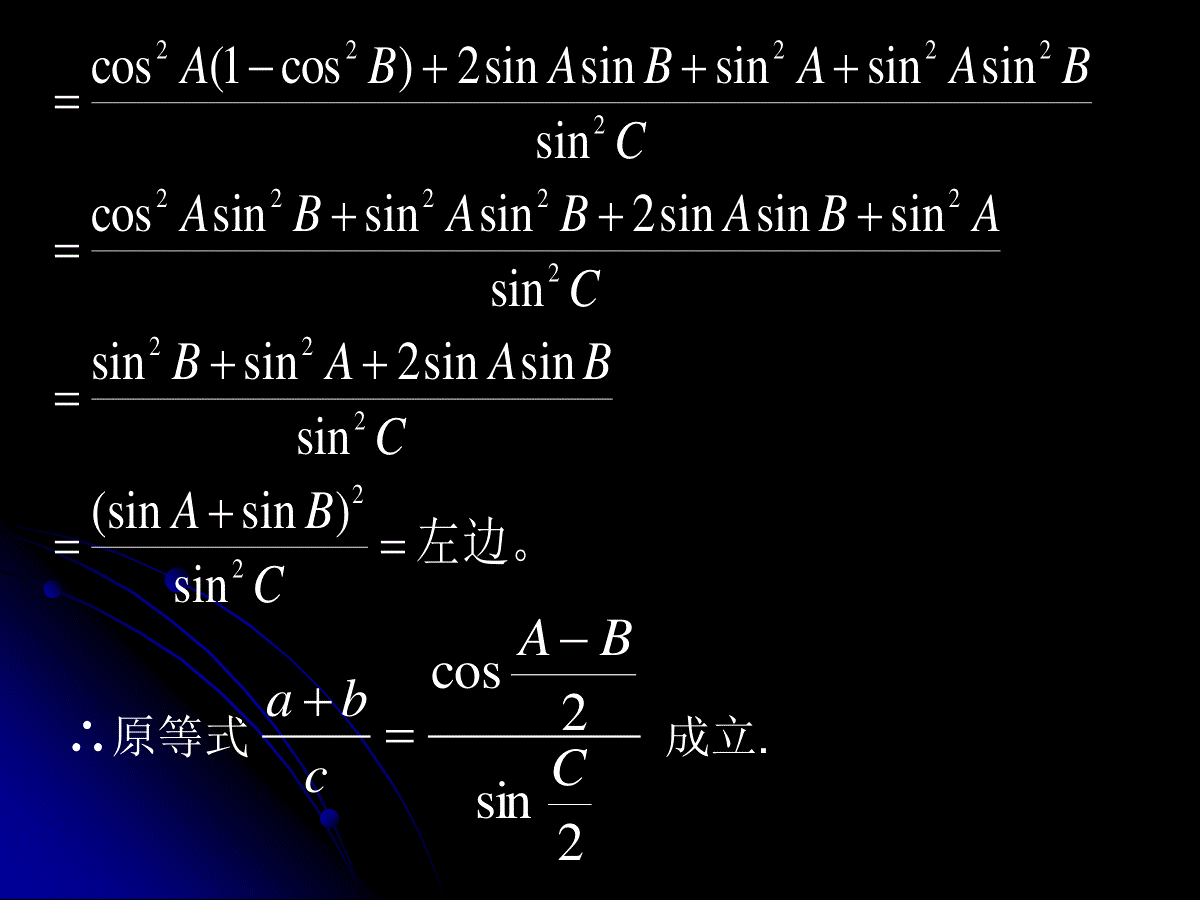
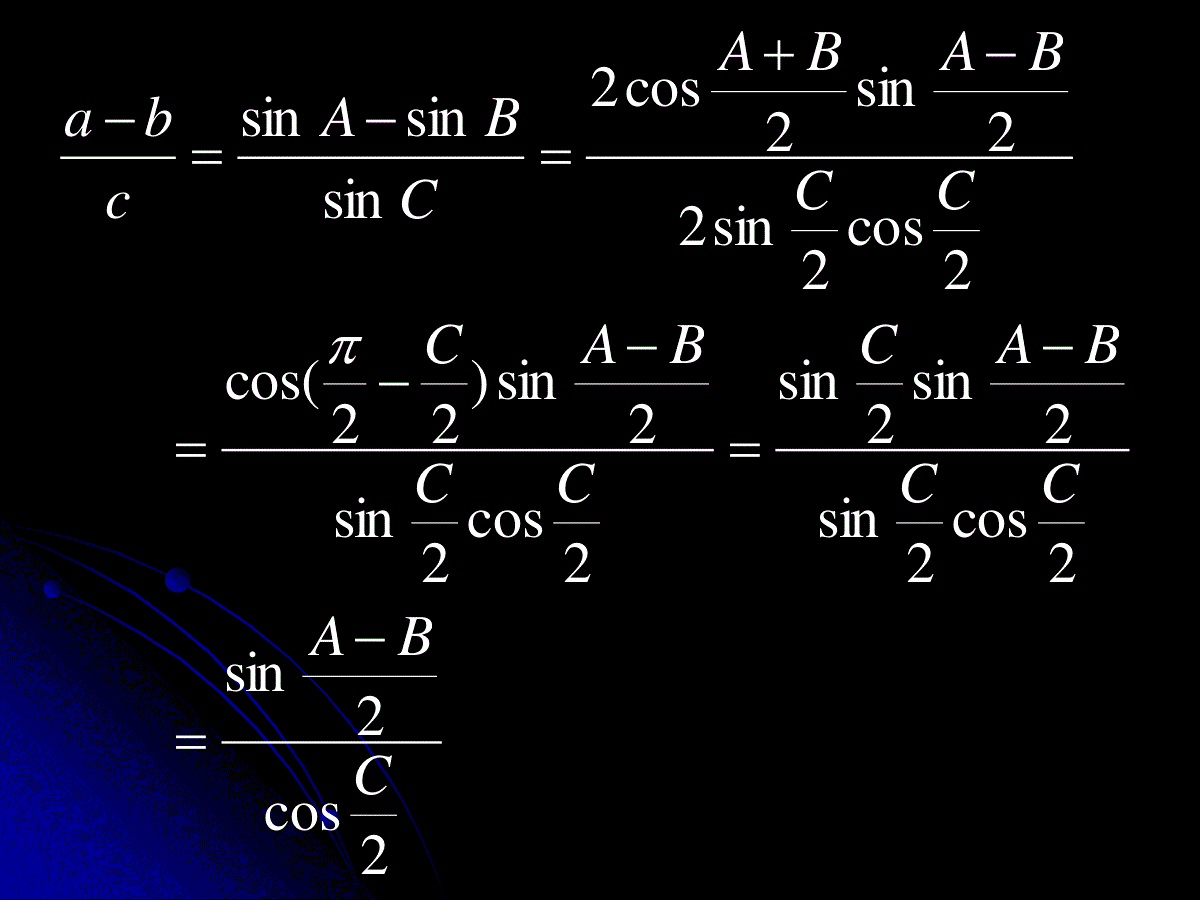
 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:正弦定理余弦定理复习题精讲
链接地址:https://www.777doc.com/doc-5525463 .html