当前位置:首页 > 建筑/环境 > 工程监理 > 理论力学第三章-刚体力学-1
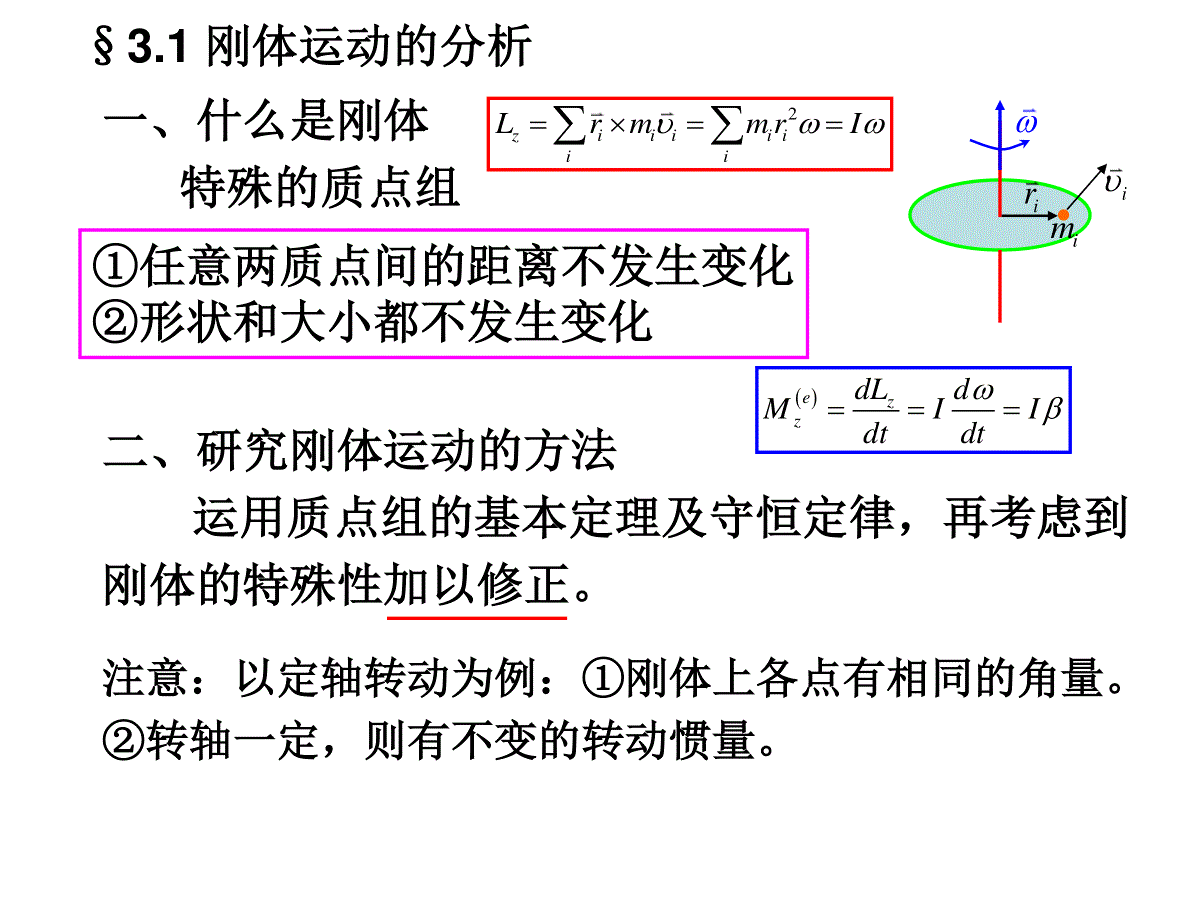
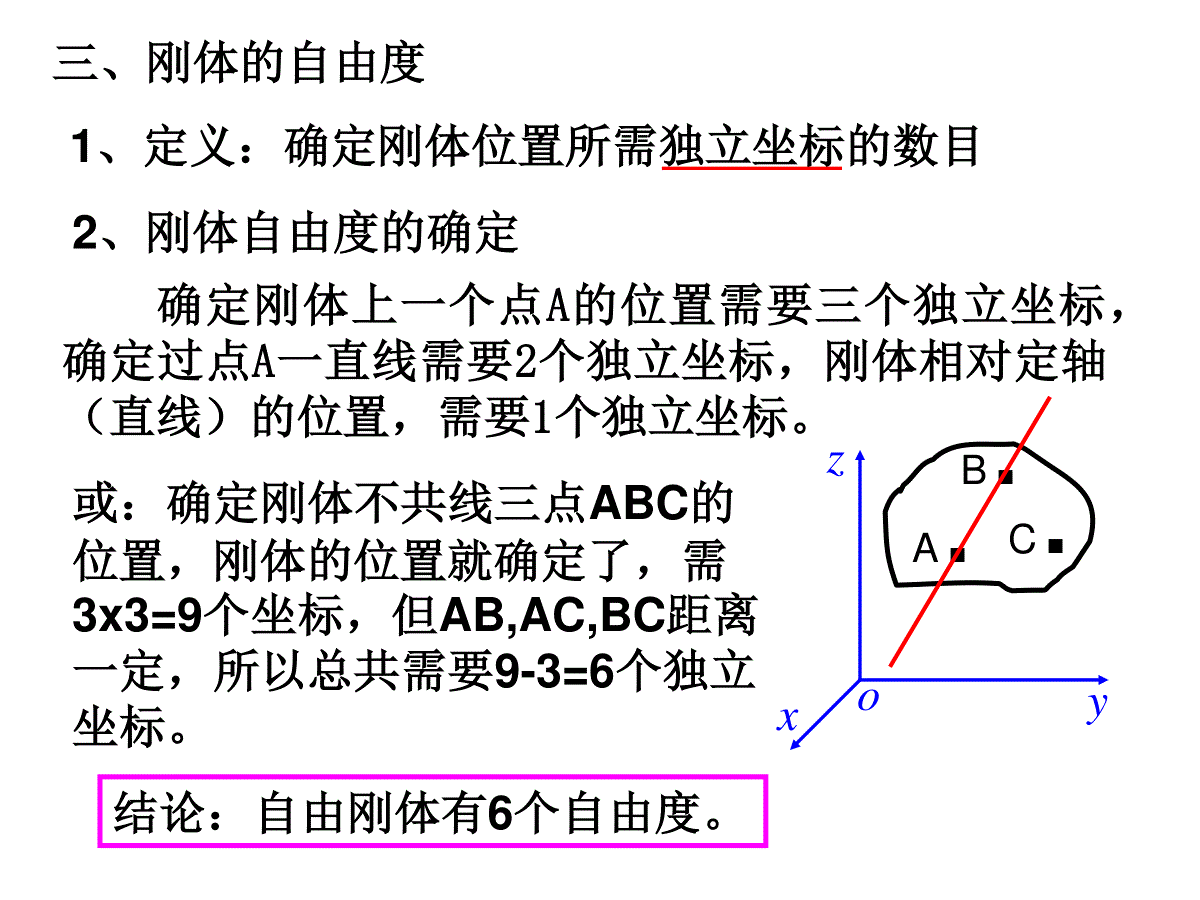
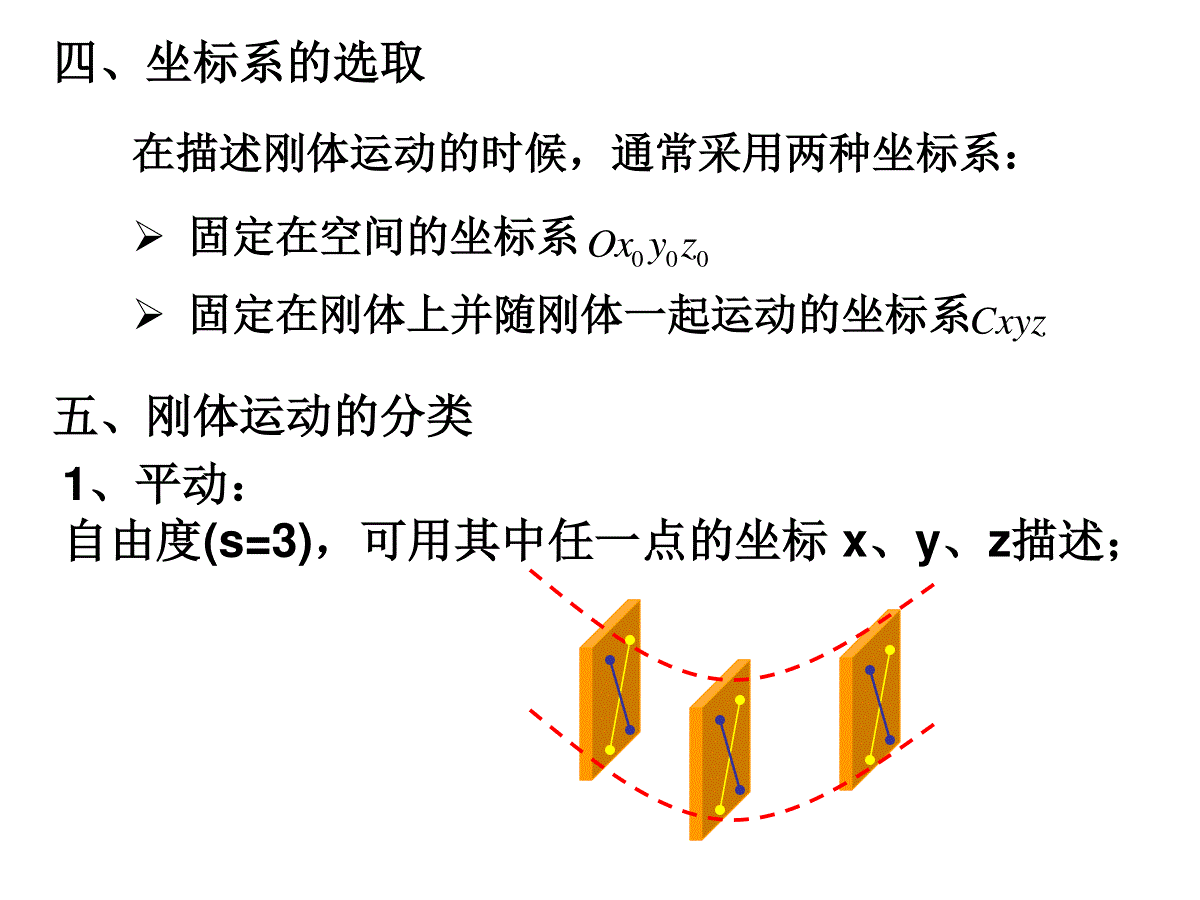
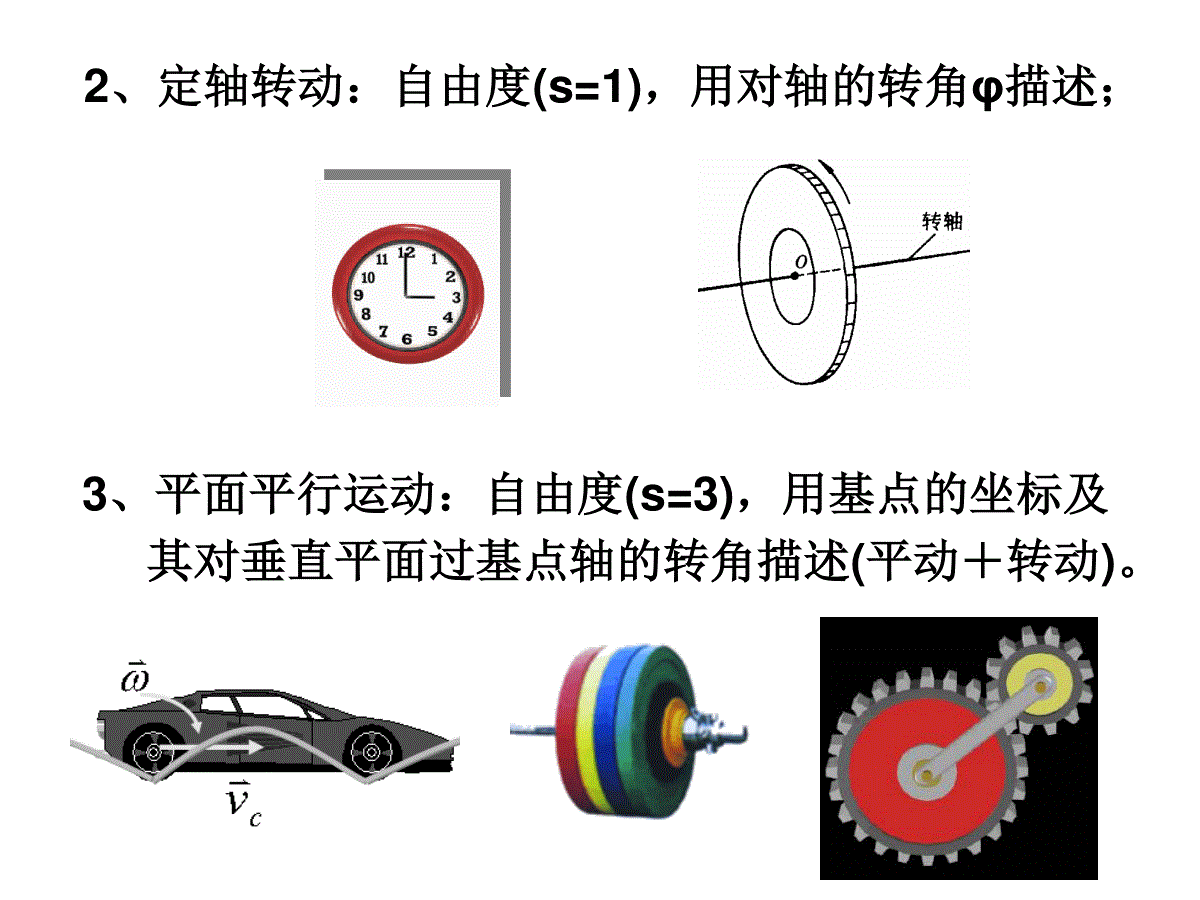
第三章刚体力学•刚体运动方程与平衡方程•刚体的定轴转动•刚体的平面平行运动•刚体的定点转动§3.1刚体运动的分析一、什么是刚体特殊的质点组①任意两质点间的距离不发生变化②形状和大小都不发生变化注意:以定轴转动为例:①刚体上各点有相同的角量。②转轴一定,则有不变的转动惯量。二、研究刚体运动的方法运用质点组的基本定理及守恒定律,再考虑到刚体的特殊性加以修正。iriim2ziiiiiiiLrmmrIezzdLdMIIdtdt三、刚体的自由度2、刚体自由度的确定确定刚体上一个点A的位置需要三个独立坐标,确定过点A一直线需要2个独立坐标,刚体相对定轴(直线)的位置,需要1个独立坐标。或:确定刚体不共线三点ABC的位置,刚体的位置就确定了,需3x3=9个坐标,但AB,AC,BC距离一定,所以总共需要9-3=6个独立坐标。结论:自由刚体有6个自由度。1、定义:确定刚体位置所需独立坐标的数目A.B.C.oxyz四、坐标系的选取在描述刚体运动的时候,通常采用两种坐标系:固定在空间的坐标系固定在刚体上并随刚体一起运动的坐标系000OxyzCxyz五、刚体运动的分类1、平动:自由度(s=3),可用其中任一点的坐标x、y、z描述;2、定轴转动:自由度(s=1),用对轴的转角φ描述;3、平面平行运动:自由度(s=3),用基点的坐标及其对垂直平面过基点轴的转角描述(平动+转动)。4、定点转动:自由度(s=3),用描述轴的方向的θ,φ角和刚体绕轴线的转角ψ描述。5、一般运动:自由度6,用描述质心位置的坐标和对质心“定点”转动的三个角(θ,φ,ψ)描述。ccczyx,,§3.2刚体运动方程与平衡方程一、空间力系的简化1、力的可传性原理力可沿它的作用线向前或向后移动,刚体运动不因力沿力的作用前后移动而改变。即:作用在刚体上的力是滑移矢量,而不是自由矢量。FF2、平衡力不改变刚体运动状态:刚体上施以一平衡力(等大,反向且作用在同一直线上)刚体运动状态不变。3、力系的简化⑴共点力系:采用平行四边形法则简化为一个单力—合力⑵共面非平行力的简化:利用力的可传性原理,将两力沿力的作用线滑移汇集于一点,再用平行四边形法则简化—合力。零力系力偶矩的特点:①力偶矩等于力偶中两力对任意一点力矩的矢量和,故:力偶矩的量值与取矩点无关。(3)平行力的简化d2F1F力偶臂:力偶中两个力的作用线之间的距离。力偶矩:力偶中任何一个力的大小与力偶臂d的乘积,方向可用右手螺旋定则确定。力偶:等大反向的一对平行力(不在同一直线上)力学效果:引起物体的转动。②只要不改变力偶矩的大小和方向,力偶可在其作用面内任意旋转、平移,也可移到与作用面平行的任意平面内,且可以同时改变力偶中力的大小与力臂的长短,对刚体的作用效果不变。结论:力偶矩是自由矢量证明:o点任取11210)(FrFrrFrFrMABBABA1F2FArBrABoABr1F1F2F2F如果刚体上有n个力偶作用,可将其力偶矩向任一点平移,按平行四边形法则合成为一个力偶矩,也就是说,诸力偶矩的矢量和就是合力偶矩。iooMM(4)一力向一点简化说明:该力和力偶矩对刚体的作用与原力等效。FAoFAo1F1FAo1FoM一力向一点o简化,得一个力和一个力偶矩,该力等于原力,该力偶矩等于原力对o点之矩。F(5)空间力系向一点简化力系中每一个力都向简化中心简化得一力和力偶矩,这些共点力和诸力偶矩可合成为一个单力和一个单力偶矩,其作用与原力系等效。结论:作用在刚体上的任意空间力系可向简化中心简化得:一个单力—主矢和一个力偶矩—主矩。)......,n21FFF(主矢:主矩:)(1iniiFrMniiFF1知识回顾力系的简化该力和力偶矩对刚体的作用与原力等效。FAoFAo1F1FAo1FoM一力向一点o简化,得一个力和一个力偶矩,该力等于原力,该力偶矩等于原力对o点之矩。F结论:作用在刚体上的任意空间力系可向简化中心简化得:一个单力—主矢和一个力偶矩—主矩。)......,n21FFF(niiFF1)(1iniiFrM【例1】如下图,将力系1F2F简化为主矢F和主矩M简化步骤:选取O为简化中心,则①将和平移至O,合成后得主矢;1F2F21FFF②在O点作的力矩的力矩,合成得到主矩:1F11FrMOA2F22FrMOB21MMM二、自由刚体的运动微分方程由质心运动定律(惯性系中)Fdtrdmc22即:zcycxcFzmFymFxm由对质心的动量矩定理(平动质心系中):①ccMdtJdczczcycycxcxMdtdJMdtdJMdtdJ即:②①、②即为刚体的基本微分方程inieirdFdT1)(③对保守力系TVE④原则上,由以上基本方程,就可以求解刚体问题,还可用动能定理(刚体中各点之间距离不变,合内力做功为0):刚体动能的微分等于各外力所做的元功之和,即:三、刚体的平衡方程2、平衡方程00000000zyxzyxMMMMFFFF1、平衡条件:主矢和主矩同时为零,若主矢,而主矩,则刚体有转动;若主矢,而主矩,则刚体有平动,故刚体的平衡条件为:。0F0M0F0M0,0MF平面力系000zyxMFF【例2】l2【例3】补充例题:有一重2Q的人字形梯子,由两个长为L的均质杆组成,DE处用无重柔绳拉住,放在光滑水平地面上,M处站一重P的人,求平衡时绳子的张力。(已知:AM=ME=1/3L,α)解:(2)受力分析,,2,BCNNQP(3)平衡方程0CzM0,0yxFFABCDEMBNCNQ2P(1)建立o-xyz坐标系xyzo以整体为研究对象受力分析:ABNTQN,,,0,0,0xyAzFFM联立方程(1)、(2)得:31()42TQPctg以AB为研究对象:BNAxNAyNQTAB对C点:22cos2coscos03BlNlQlP(1)0sin32cos2coslTlQlNB对A点:(2)2242crlcOAWANBNCB三力作用下的平衡半径为r的光滑半球形碗,固定在水平面上,一匀质棒斜靠在碗缘,一端在碗内,另一端在碗外,在碗内的长度为C,试证明棒的全长为O解:如图所示,三力作用线交于点,平衡方程为B以为基点有沿棒长方向有0ANcosWsinOOAWANBNCB02AlNsinCWcosC由两式解得2202lCsinCcos又因2221Crcossincos解得2242crlc作业-1刚体平衡:P1733.2;3.5

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:理论力学第三章-刚体力学-1
链接地址:https://www.777doc.com/doc-5827184 .html