全等三角形证明一对一辅导讲义

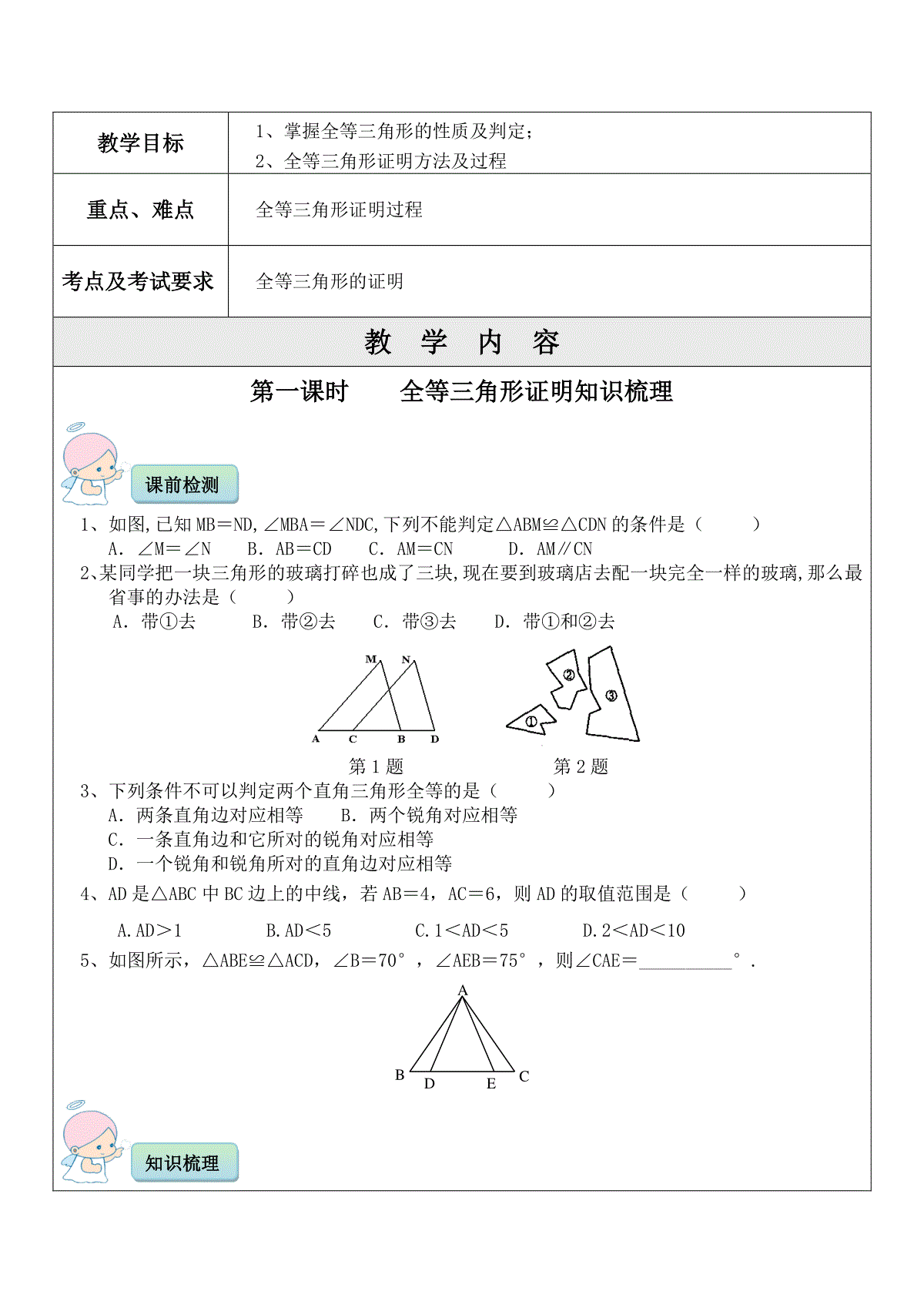
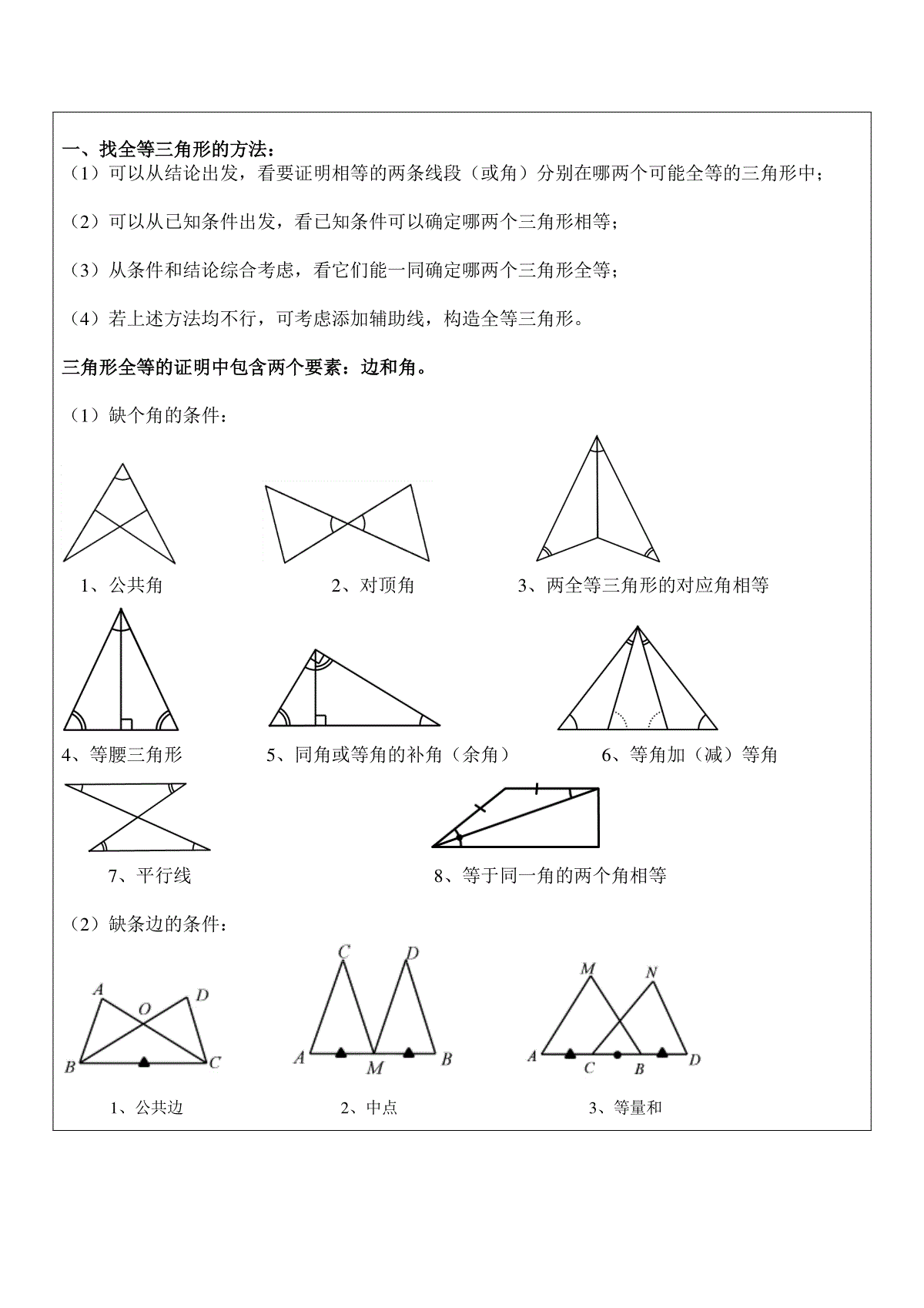
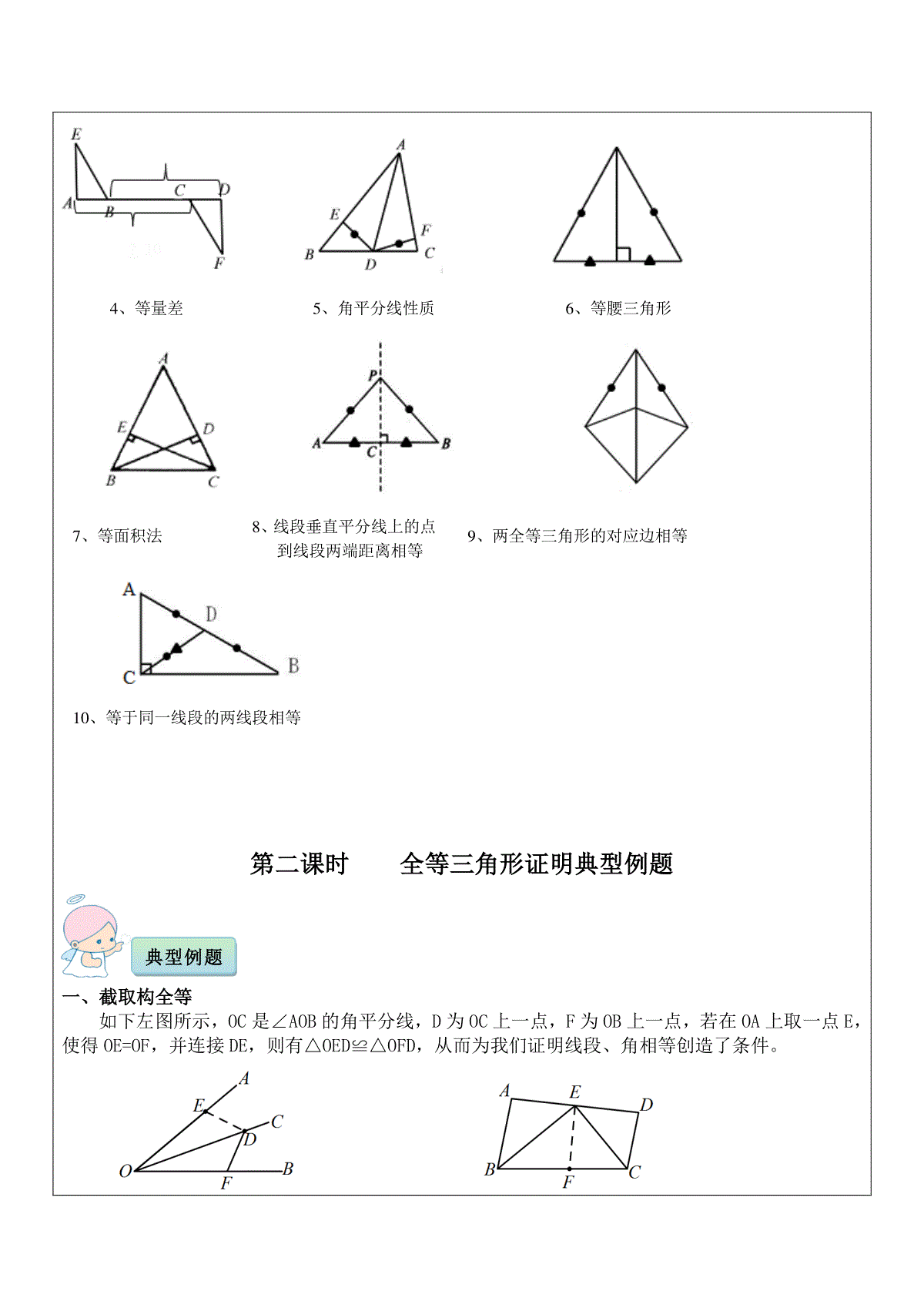
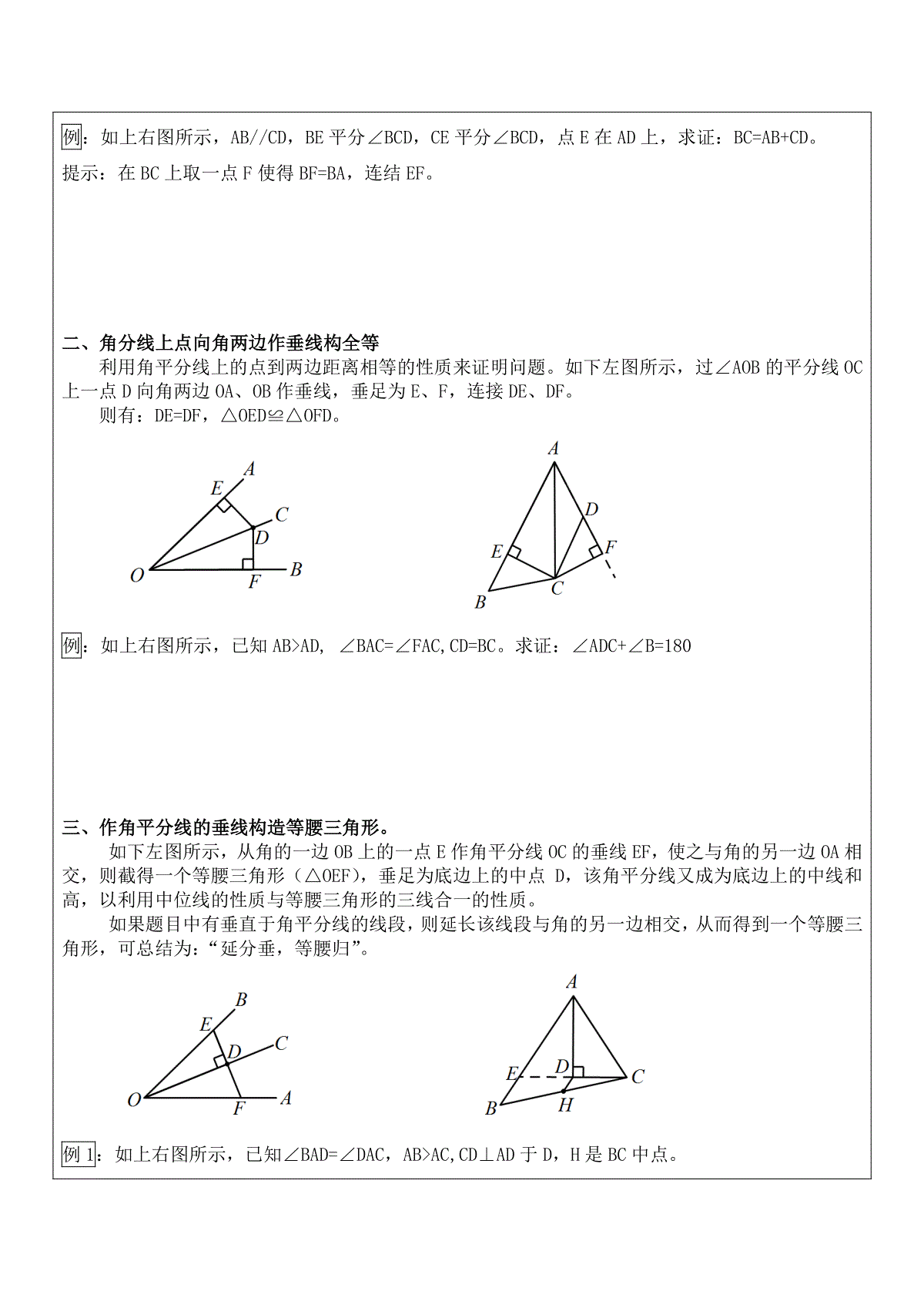
教学目标1、掌握全等三角形的性质及判定；2、全等三角形证明方法及过程重点、难点全等三角形证明过程考点及考试要求全等三角形的证明教学内容第一课时全等三角形证明知识梳理1、如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是（）A．∠M＝∠NB．AB＝CDC．AM＝CND．AM∥CN2、某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是（）A．带①去B．带②去C．带③去D．带①和②去第1题第2题3、下列条件不可以判定两个直角三角形全等的是（）A．两条直角边对应相等B．两个锐角对应相等C．一条直角边和它所对的锐角对应相等D．一个锐角和锐角所对的直角边对应相等4、AD是△ABC中BC边上的中线，若AB＝4，AC＝6，则AD的取值范围是（）A.AD＞1B.AD＜5C.1＜AD＜5D.2＜AD＜105、如图所示，△ABE≌△ACD，∠B＝70°，∠AEB＝75°，则∠CAE＝__________°.ABCDE第11题知识梳理课前检测一、找全等三角形的方法：（1）可以从结论出发，看要证明相等的两条线段（或角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形相等；（3）从条件和结论综合考虑，看它们能一同确定哪两个三角形全等；（4）若上述方法均不行，可考虑添加辅助线，构造全等三角形。三角形全等的证明中包含两个要素：边和角。（1）缺个角的条件：1、公共角2、对顶角3、两全等三角形的对应角相等4、等腰三角形5、同角或等角的补角（余角）6、等角加（减）等角7、平行线8、等于同一角的两个角相等（2）缺条边的条件：3、等量和2、中点1、公共边第二课时全等三角形证明典型例题一、截取构全等如下左图所示，OC是∠AOB的角平分线，D为OC上一点，F为OB上一点，若在OA上取一点E，使得OE=OF，并连接DE，则有△OED≌△OFD，从而为我们证明线段、角相等创造了条件。10、等于同一线段的两线段相等9、两全等三角形的对应边相等8、线段垂直平分线上的点到线段两端距离相等7、等面积法6、等腰三角形5、角平分线性质4、等量差典型例题一一例：如上右图所示，AB//CD，BE平分∠BCD，CE平分∠BCD，点E在AD上，求证：BC=AB+CD。提示：在BC上取一点F使得BF=BA，连结EF。二、角分线上点向角两边作垂线构全等利用角平分线上的点到两边距离相等的性质来证明问题。如下左图所示，过∠AOB的平分线OC上一点D向角两边OA、OB作垂线，垂足为E、F，连接DE、DF。则有：DE=DF，△OED≌△OFD。例：如上右图所示，已知ABAD,∠BAC=∠FAC,CD=BC。求证：∠ADC+∠B=180三、作角平分线的垂线构造等腰三角形。如下左图所示，从角的一边OB上的一点E作角平分线OC的垂线EF，使之与角的另一边OA相交，则截得一个等腰三角形（△OEF），垂足为底边上的中点D，该角平分线又成为底边上的中线和高，以利用中位线的性质与等腰三角形的三线合一的性质。如果题目中有垂直于角平分线的线段，则延长该线段与角的另一边相交，从而得到一个等腰三角形，可总结为：“延分垂，等腰归”。例1：如上右图所示，已知∠BAD=∠DAC，ABAC,CD⊥AD于D，H是BC中点。求证：DH=（AB-AC）提示：延长CD交AB于点E，则可得全等三角形。问题可证。例2：已知，如图，在Rt△ABC中，AB=AC，∠BAC=90o，∠1=∠2，CE⊥BD的延长线于E,求证：BD=2CE提示：延长CE交BA的延长线于点F。四、作平行线构造等腰三角形作平行线构造等腰三角形分为以下两种情况：①如下左图所示，过角平分线OC上的一点E作角的一边OA的平行线DE，从而构造等腰三角形ODE。②如下右图所示，通过角一边OB上的点D作角平分线OC的平行线DH与另外一边AO的反向延长线相交于点H，从而构造等腰三角形ODH。五、由线段和差想到的辅助线（1）遇到求证一条线段等于另两条线段之和时，一般方法是截长补短法：①截长：在长线段中截取一段等于另两条中的一条，然后证明剩下部分等于另一条；②补短：将一条短线段延长，延长部分等于另一条短线段，然后证明新线段等于长线段。截长补短法作辅助线。在△ABC中，AD平分∠BAC，∠ACB＝2∠B，求证：AB＝AC＋CD。（2）对于证明有关线段和差的不等式，通常会联系到三角形中两线段之和大于第三边、之差小于第三边，故可想办法放在一个三角形中证明。在利用三角形三边关系证明线段不等关系时，如直接证不出来，可连接两点或廷长某边构成三角形，使结论中出现的线段在一个或几个三角形中，再运用三角形三边的不等关系证明。例1：已知如图1-1：D、E为△ABC内两点,求证:AB＋AC＞BD＋DE＋CE.（法1）证明：将DE两边延长分别交AB、AC于M、N，在△AMN中，AM＋AN＞MD＋DE＋NE;（1）在△BDM中，MB＋MD＞BD；（2）在△CEN中，CN＋NE＞CE；（3）由（1）＋（2）＋（3）得：AM＋AN＋MB＋MD＋CN＋NE＞MD＋DE＋NE＋BD＋CE∴AB＋AC＞BD＋DE＋EC（法2）如图1-2，延长BD交AC于F，延长CE交BF于G，在△ABF和△GFC和△GDE中有：AB＋AF＞BD＋DG＋GF（三角形两边之和大于第三边）（1）GF＋FC＞GE＋CE（同上）………………………………（2）DG＋GE＞DE（同上）……………………………………（3）由（1）＋（2）＋（3）得：AB＋AF＋GF＋FC＋DG＋GE＞BD＋DG＋GF＋GE＋CE＋DE∴AB＋AC＞BD＋DE＋EC。六、由中点想到的辅助线在三角形中，如果已知一点是三角形某一边上的中点，那么首先应该联想到三角形的中线加倍延长中线及其相关性质（等腰三角形底边中线性质），然后通过探索，找到解决问题的方法。（1）中线把原三角形分成两个面积相等的小三角形即如图1，AD是ΔABC的中线，则SΔABD=SΔACD=SΔABC（因为ΔABD与ΔACD是等底同高的）。例1、如图2，ΔABC中，AD是中线，延长AD到E，使DE=AD，DF是ΔDCE的中线。已知ΔABC的面积为2，求：ΔCDF的面积。（2）倍长中线已知中点、中线问题应想到倍长中线，由中线的性质可知，一条中线将中点所在的线段平分，可得到一组等边，通过倍长中线又可得到一组等边及对顶角，因而可以得到一组全等三角形。如图，延长AD到E，使得AD=AE，连结BE。例2、如图5，已知ΔABC中，AD是∠BAC的平分线，AD又是BC边上的中线。求证：ΔABC是等腰三角形。七、验证中点、中线问题，应构造平行线如图，过B作BE平行AC交AD延长线于E。例3．如图3，在等腰△ABC中，AB=AC，在AB上截取BD，在AC延长线上截取CE，且使CE=BD．连接DE交BC于F．求证：DF=EF．