空间向量及其运算第4课时

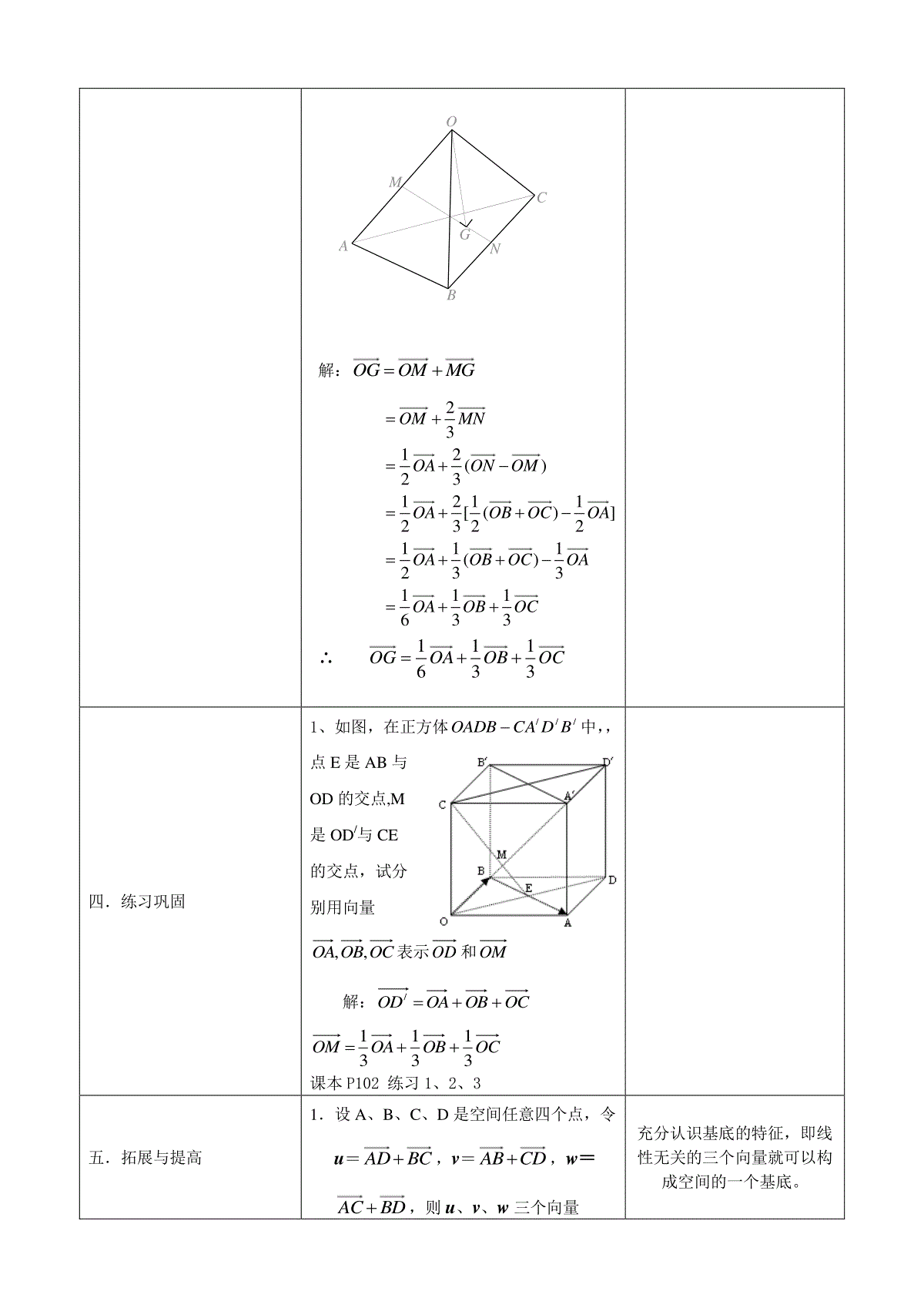
§3.1.4空间向量的正交分解及坐标表示【学情分析】：本小节首先把平面向量的基本定理推广到空间向量的基本定理奎屯王新敞新疆这种推广对学生学习已无困难奎屯王新敞新疆但仍要一步步地进行，学生要时刻牢记，现在研究的范围已由平面扩大到空间奎屯王新敞新疆这样做，一方面复习了平面向量、学习了空间向量，另一方面可加深学生的空间观念奎屯王新敞新疆让学生从二维到三维发现规律，培养学生的探索创新能力。【教学目标】：（1）知识与技能：掌握空间向量基本定理，会判断空间向量共面（2）过程与方法：正交分解推导入手，掌握空间向量基本定理（3）情感态度与价值观：认识将空间向量的正交分解，能够将空间向量在某组基上进行分解【教学重点】：空间向量正交分解，空间向量的基本定理地使用【教学难点】：空间向量的分解【课前准备】：课件【教学过程设计】：教学环节教学活动设计意图一．温故知新回顾平面向量的正交分解和平面向量的基本定理由此为基础，推导空间向量的正交分解和基本定理二．新课讲授1．空间向量的正交分解设i，j，k是空间的三个两两垂直的向量，且有公共起点O。对于空间任意一个向量OPp，设Q为点P在i，j所确定的平面上的正投影，由平面向量基本定理可知，在OQ，k所确定的平面上，存在实数z，使得kzOQOP而在i，j所确定的平面上，由平面向量基本定理可知，存在有序实数对),(yx，使得jyixOQ从而kzjyixkzOQOP由此可知，对空间任一向量p，存在一个有序实数组{zyx,,}，使得kzjyixp，称ix，jy，kz为向量p在i，j，k上的分向量。2．空间向量的基本定理如果三个向量cba,,不共面，那么对空以平面向量的基本定理为基础，层层递进，得到空间向量的正交分解形式。间任一向量p，存在一个唯一的有序实数组),,(zyx，使czbyaxp由此定理，若三向量cba,,不共面，那么空间的任一向量都可由cba,,线性表示，我们把{cba,,}叫做空间的一个基底，cba,,叫做基向量。空间任意三个不共面的向量都可以构成空间的一个基底奎屯王新敞新疆如果空间一个基底的三个基向量两两互相垂直，那么这个基底叫做正交基底，特别地，当一个正交基底的三个基向量321,,eee都是单位向量时，称这个基底为单位正交基底，对空间任一向量p，存在一个唯一的有序实数组),,(zyx，使321ezeyexp记),,(zyxp推论：设,,,OABC是不共面的四点，则对空间任一点P，都存在唯一的三个有序实数,,xyz，使OPxOAyOBzOC奎屯王新敞新疆注意介绍单位正交基、正交基、基的特殊与一般的关系，以帮助学生理解概念。三．典例讲练例1．如图，已知空间四边形OABC，其对角线,OBAC，,MN分别是对边,OABC的中点，点G在线段MN上，且2MGGN，用基底向量,,OAOBOC表示向量OG奎屯王新敞新疆向量的分解过程中注意向量的运算的正确使用。解：OGOMMG2312()231211[()]2322111()233111633OMMNOAONOMOAOBOCOAOAOBOCOAOAOBOC∴111633OGOAOBOC四．练习巩固1、如图，在正方体///BDCAOADB中，，点E是AB与OD的交点,M是OD/与CE的交点，试分别用向量OCOBOA,,表示OD和OM解：OCOBOAOD/OCOBOAOM313131课本P102练习1、2、3五．拓展与提高1．设A、B、C、D是空间任意四个点，令u＝ADBC，v＝ABCD，w＝ACBD，则u、v、w三个向量（）充分认识基底的特征，即线性无关的三个向量就可以构成空间的一个基底。ABCOMNGA．互不相等B．至多有两个相等C．至少有两个相等D．有且只有两个相等2．若a、b、c是空间的一个基底，下列各组①la、mb、nc(lmn≠0)；②a+2b、2b+3c、3a－9c；③a+2b、b+2c、c+2a；④a+3b、3b+2c、－2a+4c中，仍能构成空间基底的是（）A．①②B．②③C．①③D．②④3．已知HGFE,,,分别是空间四边形ABCD的边DACDBCAB,,,的中点，（1）用向量法证明HGFE,,,四点共面；（2）用向量法证明：BD//平面EFGH；（3）设M是EG和FH的交点，求证：对空间任一点O，有1()4OMOAOBOCOD六．小结1．正交分解的推导和空间向量基本定理2．如何将向量用坐标表示3．任意空间向量在某组基底下的分解七．作业课本P106习题3.1第6题练习与测试：（基础题）1如图，在正方体///BDCAOADB中，，点E是AB与OD的交点,M是OD/与CE的交点，试分别OMGFABCDEHEMGDCBA用向量OCOBOA,,表示OD和OM解：OCOBOAOD/OCOBOAOM3131312．设向量},,{cba是空间一个基底，则一定可以与向量baqbap,构成空间的另一个基底的向量是（）A．aB．bC．cD．ba或3．设A、B、C、D是空间任意四个点，令u＝ADBC，v＝ABCD，w＝ACBD，则u、v、w三个向量（）A．互不相等B．至多有两个相等C．至少有两个相等D．有且只有两个相等4．若a、b、c是空间的一个基底，下列各组①la、mb、nc(lmn≠0)；②a+2b、2b+3c、3a－9c；③a+2b、b+2c、c+2a；④a+3b、3b+2c、－2a+4c中，仍能构成空间基底的是（）A．①②B．②③C．①③D．②④5．设A，B，C，D是空间不共面的四点，且满足0ACAB，0ADAC，0ADAB，则△BCD是()A．钝角三角形B．直角三角形C．锐角三角形D．不确定6．已知S是△ABC所在平面外一点，D是SC的中点，若BD＝xAByACzAS，则x＋y＋z＝．7．在空间四边形ABCD中，AC和BD为对角线，G为△ABC的重心，E是BD上一点，BE＝3ED，以｛AB，AC，AD｝为基底，则GE＝．（中等题）8．已知四面体ABCD中，,,ABACAD两两互相垂直，则下列结论中，不一定成立的是（）(1).||||ABACADABACAD(2).ABCDACBDADBC(3).()0ABACADBC(4).2222||||||||ABACADABACAD不一定成立的是.9.已知非零向量21e，e不共线，如果121212,28,33ABeeACeeADee，求证：A、B、C、D共面。