当前位置:首页 > 商业/管理/HR > 企业文化 > 江苏省常州市七年级下册期末联考数学试题(有答案)
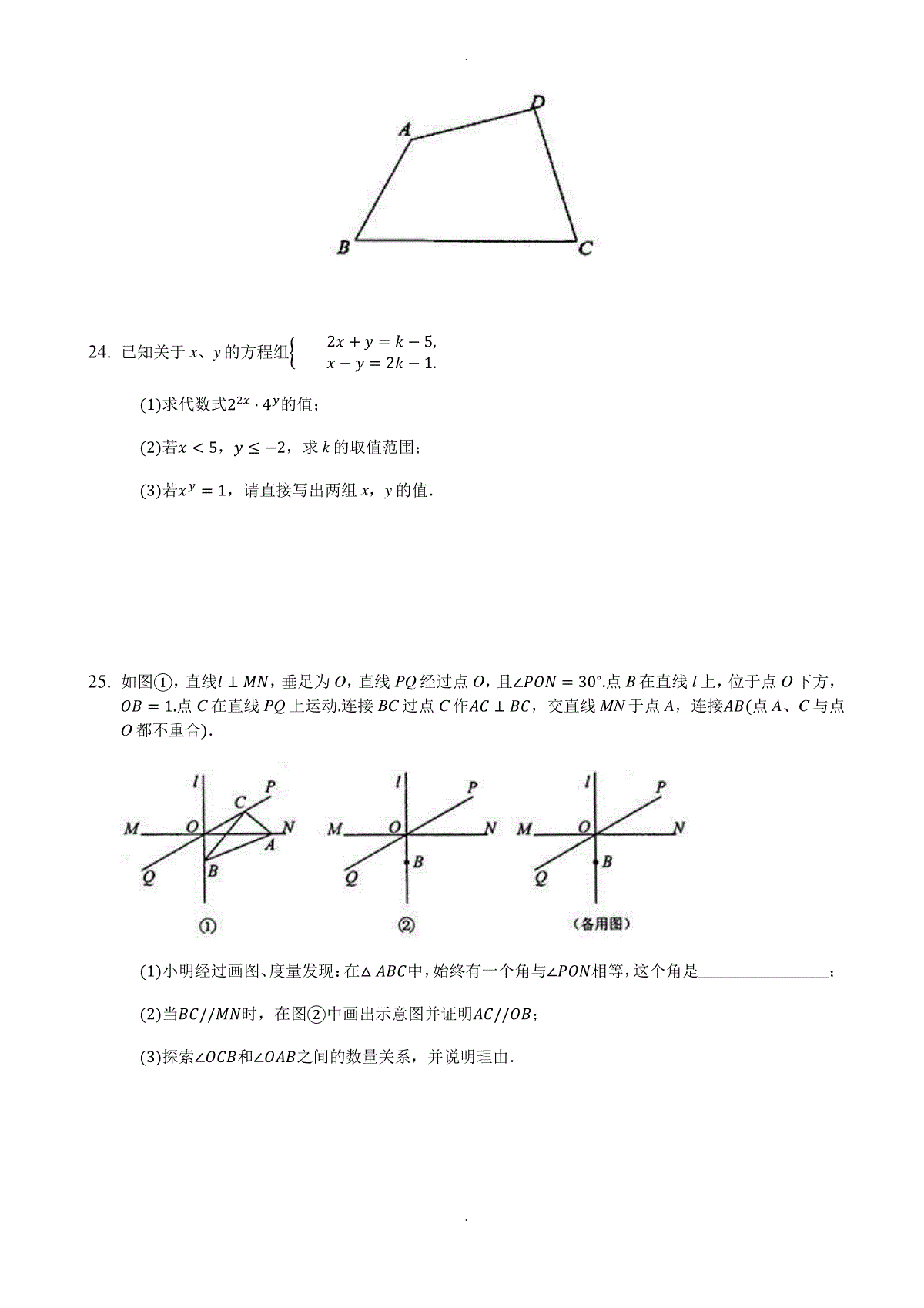
..常州市教育学会学业水平监测七年级数学试题题号一二三四总分得分一、选择题(本大题共8小题)1.下列计算中,正确的是()A.𝑥3⋅𝑥3=𝑥6B.𝑥3+𝑥3=𝑥6C.(𝑥3)3=𝑥6D.𝑥3÷𝑥3=𝑥2.下列图形中,由𝑀𝑁//𝑃𝑄,能得到∠1=∠2的是()A.B.C.D.3.不等式组{𝑥+10,𝑥1的解集在数轴上表示正确的是()A.B.C.D.4.下列各组线段能组成一个三角形的是A.4cm,6cm,11cmB.3cm,4cm,5cmC.4cm,5cm,1cmD.2cm,3cm,6cm5.若方程组{𝑥+2𝑦=1,2𝑥+𝑦=𝑎的解满足𝑥+𝑦=3,则a的值是()..A.6B.7C.8D.96.下列命题是真命题的是()A.同旁内角相等,两直线平行B.若|𝑎|=|𝑏|,则𝑎=𝑏C.如果𝑎𝑏,那么𝑎2𝑏2D.平行于同一直线的两直线平行7.《九章算术》中有这样的问题:只闻隔壁人分银,不知多少银和人;每人6两少6两,每人半斤多半斤;试问各位善算者,多少人分多少银?(注:这里的斤是指市斤,1市斤=10两)设共有x人,y两银子,下列方程组中正确的是()A.{6𝑥+6=𝑦5𝑥−5=𝑦B.{6𝑥+6=𝑦5𝑥+5=𝑦C.{6𝑥−6=𝑦5𝑥−5=𝑦D.{6𝑥−6=𝑦5𝑥+5=𝑦8.若关于x的不等式组{𝑥−𝑚0,3−2𝑥≤1所有整数解的和是10,则m的取值范围是()A.4𝑚≤5B.4𝑚5C.4≤𝑚5D.4≤𝑚≤5二、填空题(本大题共8小题)9.计算:(2𝑥−3)(𝑥+1)=________.10.分解因式:𝑥2𝑦−𝑥𝑦2=________.11.生物具有遗传多样性,遗传信息大多储存在DNA分子上.一个DNA分子的直径约为0.0000002𝑐𝑚,这个直径用科学记数法可表示为________cm.12.写出命题“互为倒数的两个数乘积为1”的逆命题:_______________________________________.13.若𝑎+𝑏=6,𝑎𝑏=7,则𝑎2+𝑏2=________.14.下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火材棒,图案②需15根火柴棒,……,按此规律,图案ⓝ需________________根火材棒.15.已知3𝑛×27=38,则n的值是________________.16.如图,已知𝐴𝐵//𝐷𝐸,∠𝐵𝐴𝐶=𝑚∘,∠𝐶𝐷𝐸=𝑛∘,则∠𝐴𝐶𝐷=________________ ∘...三、计算题(本大题共4小题)17.计算:(1)(−12)0+|3−𝜋|+(13)−2;(2)(𝑎+3)2−(𝑎+1)(𝑎−1).18.分解因式:(1)5𝑚𝑥2−20𝑚𝑦2;(2)12𝑎2𝑏+12𝑎𝑏2+3𝑏3.19.解方程组和不等式组:(1){2𝑥−𝑦=3,4𝑥−3𝑦=1;(2){3(𝑥−1)5𝑥+1,2𝑥+132𝑥−5...20.求代数式𝑥(𝑦−𝑧)−𝑦(𝑧−𝑥)+𝑧(𝑥−𝑦)的值,其中𝑥=14,𝑦=12,𝑧=−34.四、解答题(本大题共5小题)21.如图,已知点E在AB上,CE平分∠𝐴𝐶𝐷,∠𝐴𝐶𝐸=∠𝐴𝐸𝐶.求证:𝐴𝐵//𝐶𝐷.22.为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗.已知2棵A种树苗和3棵B种树苗共需270元,3棵A种树苗和6棵B种树苗共需480元.(1)𝐴、B两种树苗的单价分别是多少元⊕(2)该小区计划购进两种树苗共28棵,总费用不超过1550元,问最多可以购进A种树苗多少棵⊕23.如图,从四边形ABCD的纸片中只剪一刀,剪去一个三角形,剩余的部分是几边形⊕请画出示意图,并在图形下方写上剩余部分多边形的内角和...24.已知关于x、y的方程组{2𝑥+𝑦=𝑘−5,𝑥−𝑦=2𝑘−1.(1)求代数式22𝑥⋅4𝑦的值;(2)若𝑥5,𝑦≤−2,求k的取值范围;(3)若𝑥𝑦=1,请直接写出两组x,y的值.25.如图①,直线𝑙⊥𝑀𝑁,垂足为O,直线PQ经过点O,且∠𝑃𝑂𝑁=30∘.点B在直线l上,位于点O下方,𝑂𝐵=1.点C在直线PQ上运动.连接BC过点C作𝐴𝐶⊥𝐵𝐶,交直线MN于点A,连接𝐴𝐵(点A、C与点O都不重合).(1)小明经过画图、度量发现:在△𝐴𝐵𝐶中,始终有一个角与∠𝑃𝑂𝑁相等,这个角是________________;(2)当𝐵𝐶//𝑀𝑁时,在图②中画出示意图并证明𝐴𝐶//𝑂𝐵;(3)探索∠𝑂𝐶𝐵和∠𝑂𝐴𝐵之间的数量关系,并说明理由...常州市教育学会学业水平监测七年级数学试题答案和解析【答案】1.A2.C3.B4.B5.C6.D7.D8.A9.2𝑥2−𝑥−310.𝑥𝑦(𝑥−𝑦)11.2×10−712.如果两个数的乘积为1,那么这两个数互为倒数13.2214.(7𝑛+1)15.516.(𝑚+𝑛−180)17.解:(1)原式=1+𝜋−3+9=7+𝜋;(2)原式=𝑎2+6𝑎+9−𝑎2+1=6𝑎+10.18.解:(1)原式=5𝑚(𝑥2−4𝑦2)=5𝑚(𝑥+2𝑦)(𝑥−2𝑦);(2)原式=3𝑏(4𝑎2+4𝑎𝑏+𝑏2)=3𝑏(2𝑎+𝑏)2.19.解:(1){2𝑥−𝑦=3①4𝑥−3𝑦=1②,①×2−②,得:𝑦=5,..将𝑦=5代入①,得:2𝑥−5=3,解得:𝑥=4,∴方程组的解为{𝑥=4𝑦=5;(2){3(𝑥−1)5𝑥+1①2𝑥+132𝑥−5②,解不等式①,得:𝑥−2;解不等式②,得:𝑥4,∴不等式组的解集为−2𝑥4.20.解:原式=𝑥𝑦−𝑥𝑧−𝑦𝑧+𝑥𝑦+𝑥𝑧−𝑦𝑧=2𝑥𝑦−2𝑦𝑧=2𝑦(𝑥−𝑧),当𝑥=14,𝑦=12,𝑧=−34时,原式=2×12×(14+34)=1.21.证明:∵𝐶𝐸平分∠𝐴𝐶𝐷,∴∠𝐴𝐶𝐸=∠𝐷𝐶𝐸,又∵∠𝐴𝐶𝐸=∠𝐴𝐸𝐶,∴∠𝐷𝐶𝐸=∠𝐴𝐸𝐶,∴𝐴𝐸//𝐶𝐷.22.解:(1)设A种树苗单价为x元,B种树苗单价为y元,根据题意,得{2𝑥+3𝑦=2703𝑥+6𝑦=480,解方程组,得{𝑥=60𝑦=50,答:A种树苗单价为60元,B中树苗单为50元.(2)设购进A种树苗m棵,则购进B种树苗(28−𝑚)棵,..根据题意,得60𝑚+50(28−𝑚)≤1550,解不等式,得𝑚≤15,因为m为整数,所以m的最大值是15,答:最多可以购进A种树苗15棵.23.解:如图①,剩余的部分是三角形,其内角和为180∘,如图②,剩余的部分是四边形,其内角和为360∘,如图③,剩余的部分是五边形,其内角和为540∘.24.解:{2𝑥+𝑦=𝑘−5①𝑥−𝑦=2𝑘−1②,①+②,得3𝑥=3𝑘−6,∴𝑥=𝑘−2,把𝑥=𝑘−2代入①,得2𝑘−4+𝑦=𝑘−5,∴𝑦=−𝑘−1,∴{𝑥=𝑘−2𝑦=−𝑘−1,(1)∵{𝑥=𝑘−2𝑦=−𝑘−1,∴2𝑥+2𝑦=−6,∴22𝑥⋅4𝑦=22𝑥+2𝑦=2−6=164;(2)∵𝑥5,𝑦≤−2,∴{𝑘−25−𝑘−1≤−2,..解得1≤𝑘7;(3){𝑥=−3𝑦=0,{𝑥=1𝑦=−4.25.解:(1)∠𝐴𝐵𝐶(2)如图所示:∵𝐵𝐶//𝑀𝑁,∴∠𝐴𝑂𝐵+∠𝑂𝐵𝐶=180∘,∵∠𝐴𝑂𝐵=90∘,∴∠𝑂𝐵𝐶=90∘,∵∠𝐴𝐶𝐵=90∘,∴∠𝑂𝐵𝐶+∠𝐴𝐶𝐵=90∘+90∘=180∘,∴𝐴𝐶//𝑂𝐵.(3)如图①,设BC与OA相交于点E,在△𝑂𝐶𝐸和△𝐵𝐴𝐸中,∵∠𝑂𝐶𝐵=180∘−∠𝑂𝐸𝐶−∠𝐶𝑂𝐸,∠𝑂𝐴𝐵=180∘−∠𝐵𝐸𝐴−∠𝐴𝐵𝐸,又∠𝐶𝑂𝐸=∠𝐴𝐵𝐸=30∘,∠𝑂𝐸𝐶=∠𝐵𝐸𝐴,..∴∠𝑂𝐶𝐵=∠𝑂𝐴𝐵;如图②∠𝐴𝑂𝐶=∠𝐴𝑂𝐵+∠𝐵𝑂𝐶=90∘+60∘=150∘,∵∠𝐴𝐵𝐶=30∘,∴∠𝐴𝑂𝐶+∠𝐴𝐵𝐶=150∘+30∘=180∘,在四边形ABCO中,∠𝑂𝐶𝐵+∠𝑂𝐴𝐵=360∘−(∠𝐴𝑂𝐶+∠𝐴𝐵𝐶)=360∘−180∘=180∘,即∠𝑂𝐶𝐵和∠𝑂𝐴𝐵互补,∴∠𝑂𝐶𝐵和∠𝑂𝐴𝐵的数量关系是相等或互补.【解析】1.【分析】本题主要考查同底数幂的乘法,合并同类项,幂的乘方,同底数数幂的除法.掌握法则是解题的关键.根据同底数幂的乘法:底数不变,指数相加;合并同类项:把同类项的系数相加,字母和字母的指数不变;幂的乘方:底数不变,指数相乘;同底数幂的除法:底数不变,指数相减是解题的关键.【解答】解:𝐴.𝑥3⋅𝑥3=𝑥6,故A正确;B.𝑥3+𝑥3=2𝑥3,故B错误;C.(𝑥3)3=𝑥9,故C错误;D.𝑥3÷𝑥3=1,故D错误.故选A.2.【分析】..此题考查的是平行线的性质,根据两直线平行,同位角相等结合对顶角相等易得答案.【解答】解:𝐴.由𝑀𝑁//𝑃𝑄,能得到∠1+∠2=180∘,故不合题意;B.由𝑀𝑃//𝑁𝑄,根据两直线平行,内错角相等能得到∠1=∠2,故不合题意;C.如图:∵𝑀𝑁//𝑃𝑄,∴∠1=∠3,又∵∠2=∠3,∴∠1=∠2.故C合题意;D.观察图形∠1与∠2为同旁内角,由𝑀𝑁//𝑃𝑄,不能得到∠1=∠2,故不合题意.故选C.3.【分析】本题主要考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,再表示在数轴上即可判断.【解答】解:{𝑥+10①𝑥1②,解不等式①,得𝑥−1,解不等式②,刘𝑥1,所以不等式组的解集为−1𝑥1,不等式组的解集在数轴上表示如下:...故选B.4.【分析】此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,逐一进行分析即可.【解答】解:𝐴.∵4+611,∴不能组成三角形,故不合题意;B.∵3+45,∴能组成三角形,故合题意;C.∵4+1=5,∴不能组成三角形,故不合题意;D.∵2+36,∴不能组成三角形,故不合题意;故选B.5.【分析】此题考查的是二元一次方程组的解法以及二元一次方程组的解和一元一次方程的解法,利用加减消元法解方程组,将x,y的值用含a的代数式表示,将其代入𝑥+𝑦=3,转化为关于a的一元一次方程求解即可.【解答】解:{𝑥+2𝑦=1①2𝑥+𝑦=𝑎②,①×2−②,得:3𝑦=2−𝑎,解得:𝑦=2−𝑎3,②×2−①,得:3𝑥=2𝑎−1,解得:𝑥=2𝑎−13,∵𝑥+𝑦=3,∴2𝑎−13+2−𝑎3=3,解得:𝑎=8.故选C.6.【分析】..本题主要考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.利用平行线的判定定理,绝对值的性质,有理数的乘方进行判断即可.【解答】解:𝐴.同旁内角互补,两直线平行,故A错误;B.若|𝑎|=|𝑏|,则𝑎=±𝑏,则B错误;C.如果𝑎=1,𝑏=−2,则𝑎2𝑏2,故C错误;D.平行于同一直线的两直线平行,故D正确.故选D.7.【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题


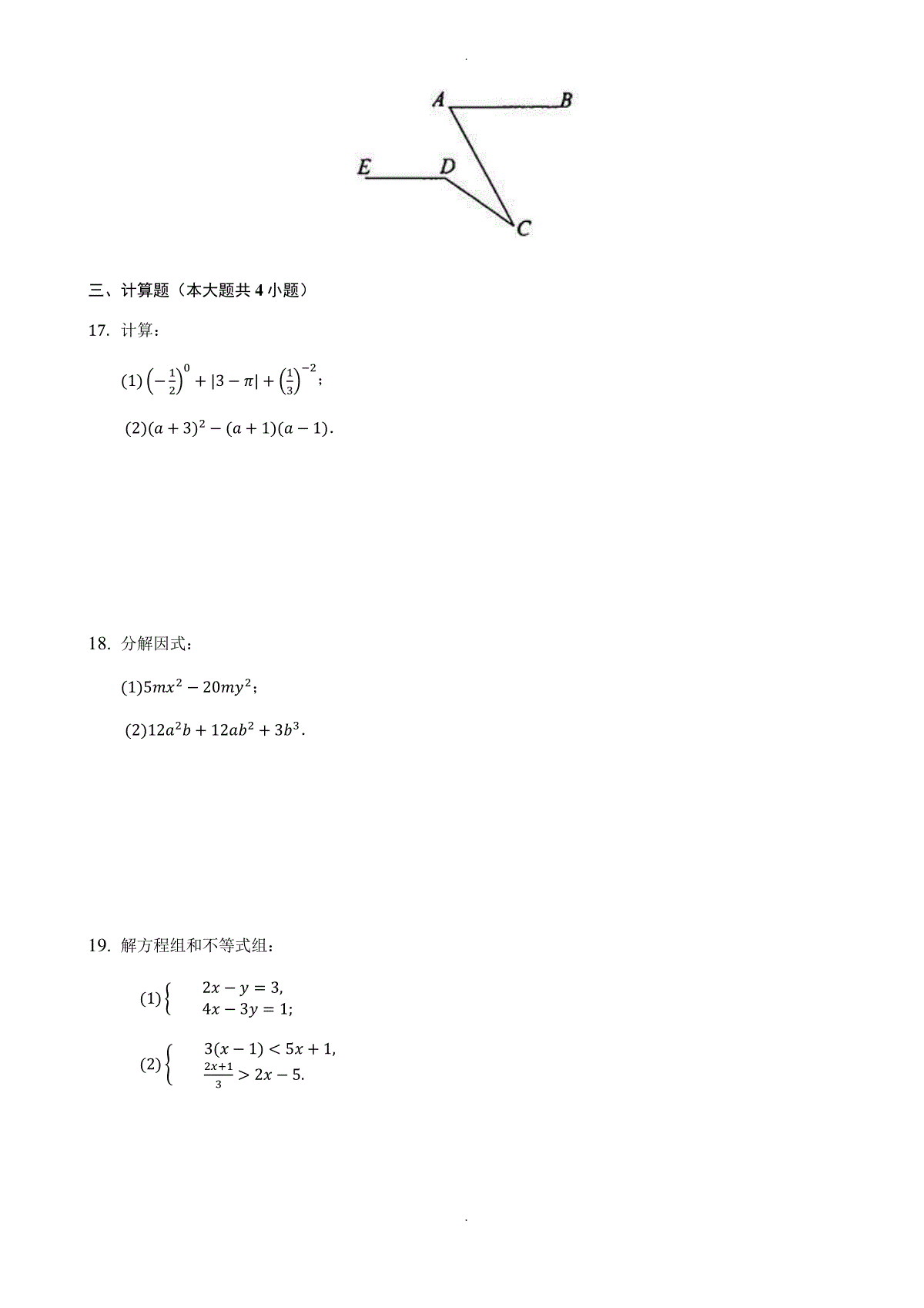

 三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
三七文档所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
本文标题:江苏省常州市七年级下册期末联考数学试题(有答案)
链接地址:https://www.777doc.com/doc-6385902 .html