2019年广东省初中学业水平考试(数学)试卷及答案

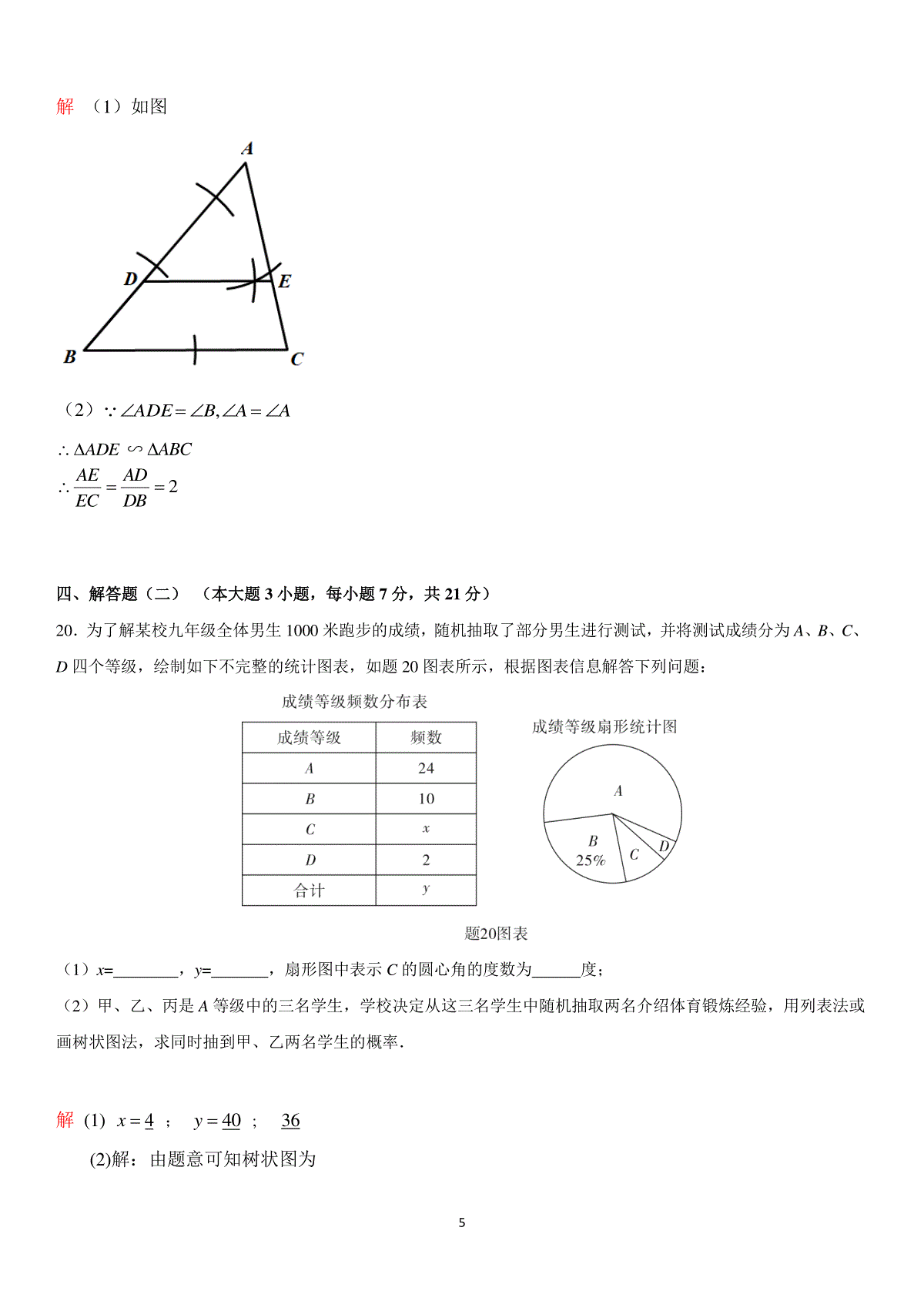
12019年广东省初中学业水平考试数学说明：1．全卷共4页，满分为120分，考试用时为100分钟．2．答卷前，考生务必用黑色字迹的签字笔或钢笔在答题卡填写自己的准考证号、姓名、考场号、座位号．用2B铅笔把对应该号码的标号涂黑．3．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．4，非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液．不按以上要求作答的答案无效．5．考生务必保持答题卡的整洁．考试结束时，将试卷和答题卡一并交回．一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．1．-2的绝对值是（A）A．2B．-2C．12D．±22．某网店2019年母亲节这天的营业额为221000元，将数221000用科学记数法表示为（B）A．2.21×106B．2.21×105C．221×103D．0.221×1063．如图，由4个相同正方体组合而成的几何体，它的左视图是（A）4．下列计算正确的是（C）A．632bbbB．339bbbC．2222aaaD．363aa5．下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（C）6．数据3、3、5、8、11的中位数是（C）A．3B．4C．5D．67．实数a、b在数轴上的对应点的位置如图所示，下列式子成立的是（D）2A．abB．abC．0abD．0ab8．化简24的结果是（B）A．-4B．4C．±4D．29．已知1x、2x是一元二次方程220xx的两个实数根，下列结论错误．．的是（D）A．12xxB．2112=0xxC．12=2xxD．12=2xx10．如图，正方形ABCD的边长为4，延长CB至E使EB=2，以EB为边在上方作正方形EFGB，延长FG交DC于M，连接AM、AF，H为AD的中点，连接FH分别与AB、AM交于点N、K．则下列结论：ANHGNF①≌△△；AFNHFG②；2FNNK③；:1:4AFNADMSS④△△．其中正确的结论有（C）A．1个B．2个C．3个D．4个二、填空题（本大题6小题，每小题4分，共24分）请将下列各题的正确答案填写在答题卡相应的位置上．11．计算：10120193=．答案：4解析：本题考查了零次幂和负指数幂的运算12．如图，已知ab，175°，则∠2＝．答案：105解析：本题考查了平行线的性质，互为补角的计算313．一个多边形的内角和是1080，这个多边形的边数是．答案：8解析：本题考查了多边形内角和的计算公式14．已知23xy，则代数式489xy的值是．答案：21解析：整体思想，考查了整式的运算15．如图，某校教学楼AC与实验楼BD的水平间距CD=153米，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，则教学楼AC的高度是米（结果保留根号）．答案：15153解析：本题利用了特殊三角函数值解决实际问题16．如题16-1图所示的图形是一个轴对称图形，且每个角都是直角，长度如图所示，小明按题16-2图所示方法玩拼图游戏，两两相扣，相互间不留空隙，那么小明用9个这样的图形（题16-1图）拼出来的图形的总长度是（结果用含a、b代数式表示）．答案：8ab解析：本题考查了轴对称图形的性质，根据题目找规律三、解答题（一）（本大题3小题，每小题6分，共18分）417．解不等式组：12214xx①②解①21xx3②4)1(2x422x22x1x∴该不等式组的解集是x318．先化简，再求值：221224xxxxxx，其中=2x．解原式=)1()2)(2(21xxxxxx=xx2当2x原式=222=2222=2119．如图，在ABC△中，点D是AB边上的一点．（1）请用尺规作图法，在ABC△内，求作∠ADE，使∠ADE=∠B，DE交AC于E；（不要求写作法，保留作图痕迹）（2）在（1）的条件下，若2ADDB，求AEEC的值．5解（1）如图（2）AABADE,ADE∽ABC2DBADECAE四、解答题（二）（本大题3小题，每小题7分，共21分）20．为了解某校九年级全体男生1000米跑步的成绩，随机抽取了部分男生进行测试，并将测试成绩分为A、B、C、D四个等级，绘制如下不完整的统计图表，如题20图表所示，根据图表信息解答下列问题：（1）x=，y=，扇形图中表示C的圆心角的度数为度；（2）甲、乙、丙是A等级中的三名学生，学校决定从这三名学生中随机抽取两名介绍体育锻炼经验，用列表法或画树状图法，求同时抽到甲、乙两名学生的概率．解(1)4x；40y;36(2)解：由题意可知树状图为6由树状图可知，同时抽到甲、乙两名学生的概率为21=63答：同时抽到甲、乙两名学生的概率为13。21．某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，已知每个篮球的价格为70元，每个足球的价格为80元．（1）若购买这两类球的总金额为4600元，求篮球、足球各买了多少个？（2）若购买篮球的总金额不超过购买足球的总金额，求最多可购买多少个篮球？解(1)方法一：解：设计划购买篮球x个，足球y个由题意得，6070804600xyxy解得：2040xy答：计划购买篮球20个，足球40个.方法二：解：设计划购买篮球x个，则购买足球(60)x个由题意得，7080(60)4600xx解得：20x则60602040x答：计划购买篮球20个，足球40个.(2)解：设计划购买篮球a个，则购买足球(60)a个则有7080(60),(060)aaa解得：032a答：最多可购买32个篮球。22．在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫格点，ABC△的三个顶点均在格点上，7以点A为圆心的EF与BC相切于点D，分别交AB、AC于点E、F．（1）求ABC△三边的长；（2）求图中由线段EB、BC、CF及FE所围成的阴影部分的面积．解（1）由图可知102406222AB102406222AC54808422BC（2）由（1）可知102AB，102AC，54BC222BCACAB90BAC又DBCA相切于点为圆心的圆与以点∵5221BCADBDCDBCAD，2010210221ABCS2)52(4120阴S204120520五、解答题（三）（本大题3小题，每小题9分，共27分）23．如图，一次函数y=k1x+b的图象与反比例函数2kyx的图象相交于A、B两点，其中点A的坐标为（-1，4），点B的坐标为（4，n）．8（1）根据图象，直接写出满足21kkxbx的x的取值范围；（2）求这两个函数的表达式；（3）点P在线段AB上，且:1:2AOPBOPSS，求点P的坐标．解（1）由已知得：1x或40x（2）xky2经点)4,1(A24k，解得42kxy4当4x时，得144y)1,4(B将)1,4(),4,1(BA代入bxky1得bkbk11414解得311bk3xy反比例函数为xy4一次函数为3xy（3）∵𝑆△𝐴𝑂𝑃：𝑆△𝐵𝑂𝑃=1：2，∴AP:BP=1:2；∵A（-1，4），B（4，-1），9∴AB=√（4+1）2+（−1−4）2=5√2；∴AP=13𝐴𝐵=5√23设点P（t，-t+3）∵P在线段AB上，∴−1＜t＜4；∴AP=√（t+1）2+（−t+3−4）2=√2t2+4t+2=5√23解得：𝑡1=23；𝑡2=−83（舍去）；∴P（23，73）；∴当𝑆△𝐴𝑂𝑃：𝑆△𝐵𝑂𝑃=1：2时，P（23，73）24．如题24-1图，在ABC中，AB=AC，⊙O是ABC△的外接圆，过点C作∠BCD=∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF=AC，连接AF．（1）求证：ED=EC；（2）求证：AF是⊙O的切线；（3）如题24-2图，若点G是ACD的内心，25BCBE，求BG的长．解（1）∵AB=AC∴弧AB=弧AC,∠B=∠ACB∴∠D=∠B又∵∠BCD=∠ACB∴∠D=∠BCD∴ED=EC10（2）证明：连接AO,交BC于点H∵AB=AC∴A为弧BC中点∴OA⊥BC∵∠ACD=∠F＋∠FAC又∵∠ACB=∠BCD,∠F=∠CAF∴∠CAF=∠ACB∴AF∥BC∴∠FAO=∠CHO=90°即AO⊥AF又∵A在圆上，∴AF为⊙O的切线（3）连接AG由（2）知AF∥BC∴∠FAG=∠AGB∵G为△ACD的内心∴AG平分∠DAC∴∠EAG=∠CAG又∵∠BAE=∠BCD=∠CAF∴∠FAC+∠CAG=∠BAE+∠EAG∴∠BAG=∠BGA∴AB=BG∵∠B=∠B,∠BAE=∠ACB∴△AEB∽△CAB∴BCABABEB即BCBEAB2∵EB·BC=25,AB=BG∴BG=AB=525．如题25-1图，在平面直角坐标系中，抛物线233373848yxx与x轴交于点A、B（点A在点B右侧），点D为抛物线的顶点．点C在y轴的正半轴上，CD交x轴于点F，CAD△绕点C顺时针旋转得到CFE△，点A恰好旋转到点F，连接BE．11（1）求点A、B、D的坐标；（2）求证：四边形BFCE是平行四边形；（3）如题25-2图，过顶点D作1DDx轴于点D1，点P是抛物线上一动点，过点P作PMx轴，点M为垂足，使得PAM△与1DDA△相似（不含全等）．①求出一个满足以上条件的点P的横坐标；②直接回答．．．．这样的点P共有几个？解（1）依题意837433832xxy令0y得：0837433832xx........①解得：71x，12x)0,7(B,)0,1(A把3832433x代入①得：32y)32,3(D（2）由（1）得：B（-7，0）A（1，0），D(-3,-32)由题意可知，△CAD≌△CFE12∴CF=AC又CO⊥AF∴0A=0F∴F(-1,0)∴AF=2∴设DF解析式为y=kx＋bbkbk3320所以：k=3b=3∴y=3x＋3令x=0得y=3∴C(0,3)∴AC=22)3(1=2∴AC=AF=CF∴△ACF为等边三角形∴∠CAF=60°∵△CAD≌△CFE∴∠ACF=∠FCE=60°，CD=CE又∠ECA+∠CAF=180°∴CE∥AB又BF=6CD=22)323(3=6∴BF=CE∴四边形BFCE为平行四边形（3）①当P在下方时，∵1190DADPAMADD且当ADD1∽AMP时；∴ADMADDPM11由（1）可知：A（1，0）D（-3，-23）)0,3(1D设)83743383,(2mmmP；则M（m,0）13∴83743383)83743383(022mmmmPM32)32(01DDmMAAD1;4)3(11根据ADMADDPM11得：3214837433832mmm整理得：05232mm∴（3m+5）（m-1）=0∴1,35mm（舍）∴P的横坐标为35②P共有3个．