直线与方程复习课

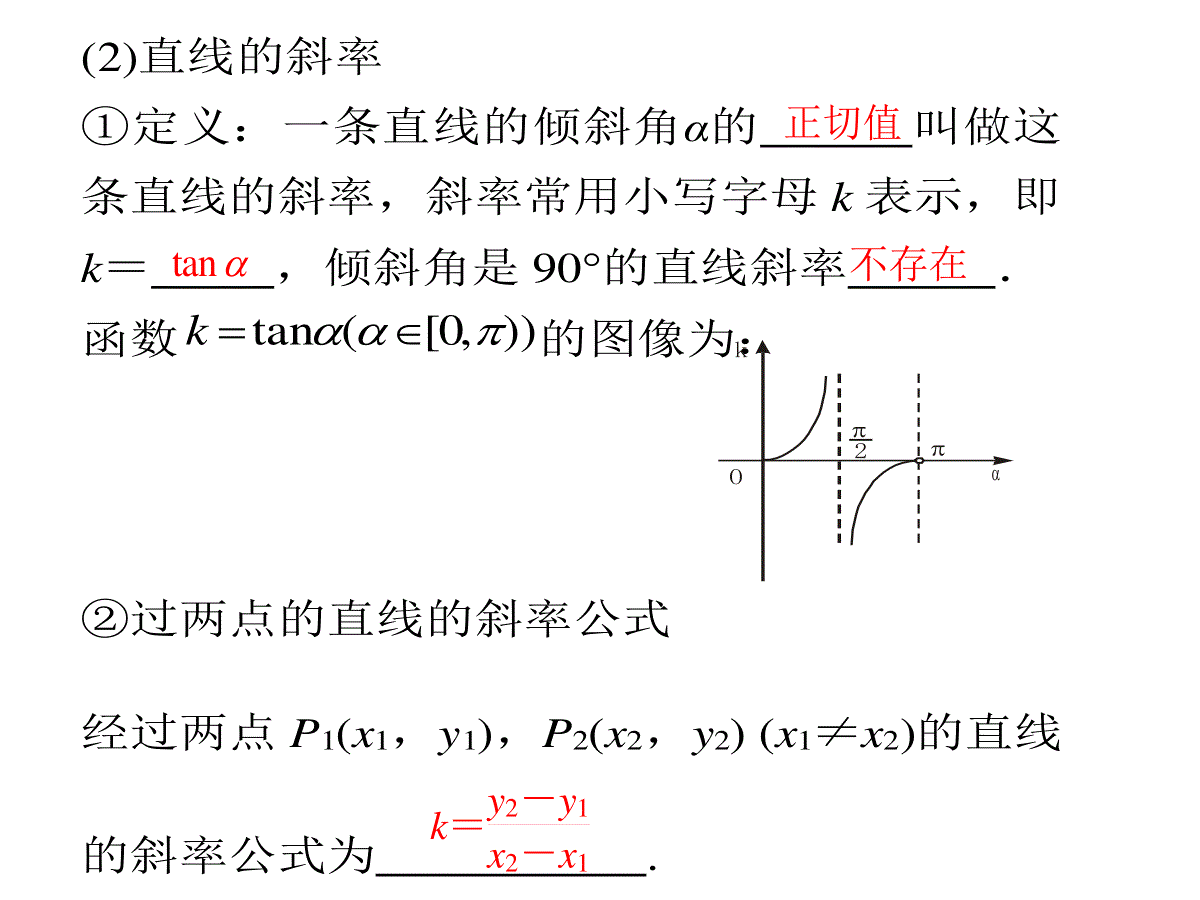
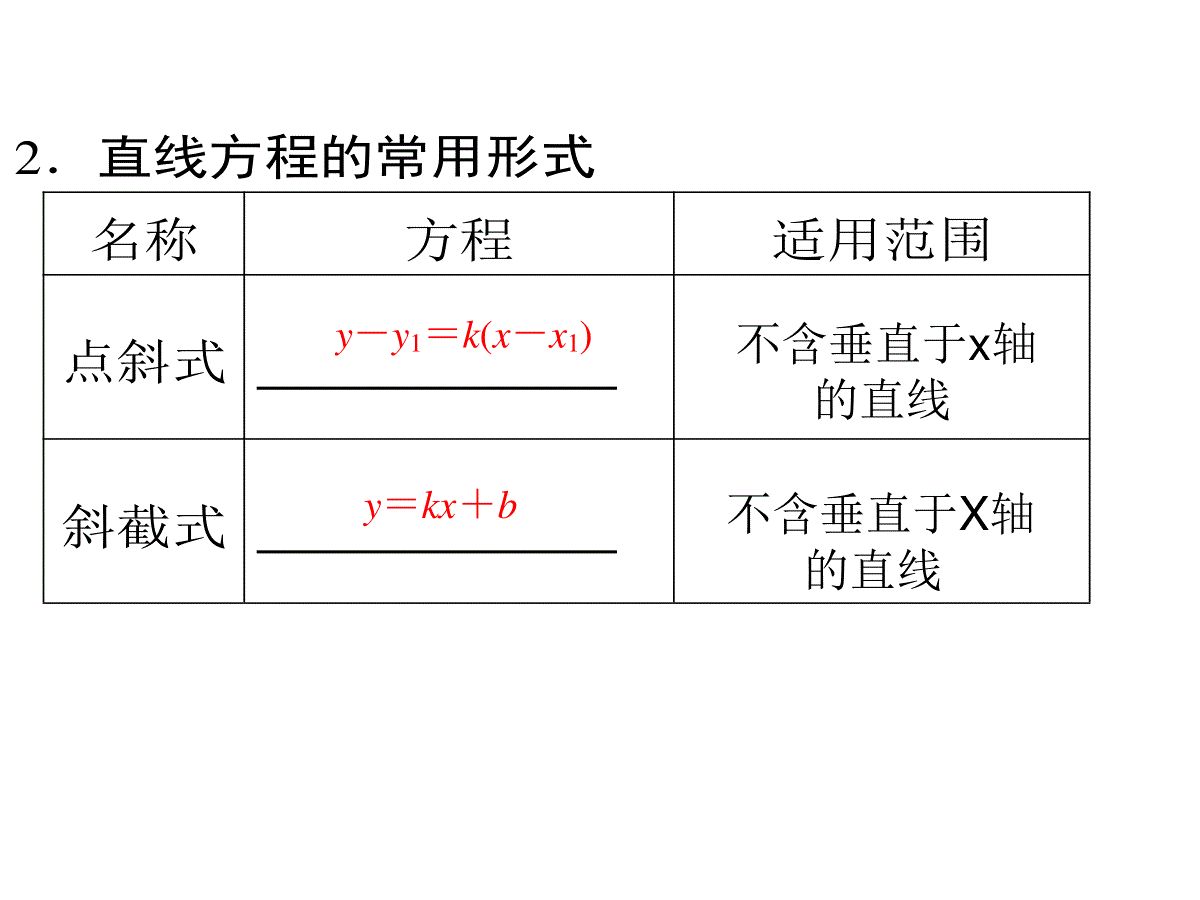
直线与方程复习（第一讲）•大邑中学高二年级数学组熊康考点要求•1．考查直线的有关概念，如直线的倾斜角、斜率、截距等；考查过两点的斜率公式．•2．求不同条件下的直线方程(点斜式、截距式及一般式等)．•3．本讲是解析几何的基础，复习时要掌握直线方程的几种形式及相互转化的关系，会根据已知条件求直线方程．•4．注意熟练地画出图形，抓住图形的特征量，利用该特征量解决问题往往能达到事半功倍.要点梳理1．直线的倾斜角与斜率(1)直线的倾斜角①定义：当直线l与x轴相交时，我们取x轴作为基准，x轴与直线l方向之间所成的角α叫做直线l的倾斜角．当直线l与x轴平行或重合时，规定它的倾斜角为.②倾斜角的范围为.正向0°0°≤α180°向上的基础知识自主学习(2)直线的斜率①定义：一条直线的倾斜角α的叫做这条直线的斜率，斜率常用小写字母k表示，即k＝，倾斜角是90°的直线斜率．函数)),0[(tank的图像为：②过两点的直线的斜率公式经过两点P1(x1，y1)，P2(x2，y2)(x1≠x2)的直线的斜率公式为.正切值tank＝y2－y1x2－x1不存在kO22．直线方程的常用形式名称方程适用范围点斜式斜截式y－y1＝k(x－x1)y＝kx＋b不含垂直于x轴的直线不含垂直于X轴的直线截距式一般式xa＋yb＝1Ax＋By＋C＝0(A2＋B2≠0)不含垂直于坐标轴和过原点的直线平面直角坐标系内的直线都适用3.过P1(x1，y1)，P2(x2，y2)的直线方程(1)若x1＝x2，且y1≠y2时，直线垂直于x轴，方程为；(2)若x1≠x2，且y1＝y2时，直线垂直于y轴，方程为；(3)若x1＝x2＝0，且y1≠y2时，直线即为y轴，方程为；(4)若x1≠x2，且y1＝y2＝0时，直线即为x轴，方程为.1xx1yyx=0y=04．线段的中点坐标公式若点P1、P2的坐标分别为(x1，y1)、(x2，y2)，且线段P1P2的中点M的坐标为(x，y)，则，此公式为线段P1P2的中点坐标公式．222121yyyxxx(1)直接法：选择适当形式的直线方程，直接求出方程中的系数。(2)待定系数法：选择适当的直线方程设出目标方程，构造关于系数的方程(组)求系数。5.求直线方程的一般方法：基础自测1．过点M(－2，m)，N(m,4)的直线的斜率等于1，则m的值为________．1解析∵kMN＝m－4－2－m＝1，∴m＝1.2．若点A(4,3)，B(5，a)，C(6,5)三点共线，则a的值为______．4解析∵kAC＝5－36－4＝1，kAB＝a－35－4＝a－3.由于A、B、C三点共线，所以a－3＝1，即a＝4.3．过点M(3，－4)，且在两坐标轴上的截距相等的直线的方程为．x＋y＋1＝0或4x＋3y＝0解析①若直线过原点，则k＝－43，∴y＝－43x，即4x＋3y＝0.②若直线不过原点．设xa＋ya＝1，即x＋y＝a.∴a＝3＋(－4)＝－1，∴x＋y＋1＝0.4．已知直线l经过点P(－2,5)，且斜率为－34，则直线l的方程为()A．3x＋4y－14＝0B．3x－4y＋14＝0C．4x＋3y－14＝0D．4x－3y＋14＝0A解析由y－5＝－34(x＋2)，得：3x＋4y－14＝0，故选A.5．已知点M是直线033:yxl与x轴的交点，将直线l绕点M旋转30后，所得的直线方程为。03x033yx或题型分类深度剖析题型一直线的倾斜角与斜率例1已知直线l过点P(－1,2)，且与以A(－2，－3)，B(3，0)为端点的线段相交，求直线l的斜率的取值范围．解方法一如图所示，直线PA的斜率kPA＝)2(1)3(2＝5，直线PB的斜率kPB＝)1(320＝－12.当直线l绕着点P由PA旋转到与y轴平行的位置PC时，它的斜率变化范围是[5，＋∞)；当直线l绕着点P由PC旋转到PB的位置时，它的斜率的变化范围是－∞，－12.∴直线l的斜率的取值范围是－∞，－12∪[5，＋∞)．方法二设直线l的斜率为k，则直线l的方程为y－2＝k(x＋1)，即kx－y＋k＋2＝0.∵A、B两点在直线的两侧或其中一点在直线l上，∴(－2k＋3＋k＋2)(3k－0＋k＋2)≤0，即(k－5)(4k＋2)≥0，∴k≥5或k≤－12.即直线l的斜率k的取值范围是－∞，－12∪[5，＋∞)．变式训练1已知两点)0,1(),2,3(BA，过点)4,3(P的直线l与线段AB有公共点，求直线l的斜率的取值范围。．【答案】]21,1[本题型小结包括垂直取两边，没有垂直取中间题型二求直线的方程例2求适合下列条件的直线方程：(1)经过点P(3,2)，且与直线013yx平行；(2)过点A(－1，－3)，倾斜角是直线y＝2x的倾斜角的21；思维启迪：选择适当的直线方程形式，把所需要的条件求出即可．变式训练2在△ABC中，已知A(5，－2)、B(7,3)，且AC边的中点M在y轴上，BC边的中点N在x轴上，求：(1)顶点C的坐标；(2)直线MN的方程．解(1)设C(x0，y0)，则AC中点M5＋x02，y0－22，BC中点N7＋x02，y0＋32.∵M在y轴上，∴5＋x02＝0，x0＝－5.∵N在x轴上，∴y0＋32＝0，y0＝－3，即C(－5，－3)．(2)∵M0，－52，N(1,0)．∴直线MN的方程为x1＋y－52＝1.即5x－2y－5＝0.本题型小结：1.选择适当的方法，选择适当的形式2.涉及斜率注意存在与否，涉及截距注意是否为零题型三直线方程的综合应用例3已知直线l经过点P(－5，－4)，且与两坐标轴围成的三角形面积为5，求直线l的方程．注意斜率不是距离解由题意知直线不过原点，且与两坐标轴都相交，可设直线l的方程为xa＋yb＝1，∵直线l过点P(－5，－4)，∴－5a＋－4b＝1，即4a＋5b＝－ab.又由已知有12|a|·|b|＝5，即|ab|＝10，解方程组4a＋5b＝－ab，|ab|＝10得a＝－52，b＝4或a＝5，b＝－2.故所求直线l的方程为x－52＋y4＝1或x5＋y－2＝1.即8x－5y＋20＝0或2x－5y－10＝0.变式训练3直线l经过点P(3,2)，且与x、y轴的正半轴交于A、B两点，且△AOB的面积最小(O为坐标原点)，求直线l的方程．解方法一设直线方程为xa＋yb＝1(a0，b0)，点P(3,2)代入得3a＋2b＝1≥26ab，得ab≥24，从而S△AOB＝12ab≥12，当且仅当3a＝2b时等号成立，这时k＝－ba＝－23，从而所求直线方程为2x＋3y－12＝0.方法二设直线方程为xa＋yb＝1(a0，b0)，点P(3,2)代入得3a＋2b＝1，解得b＝2aa－3(a3)，则S△AOB＝12ab＝a2a－3＝(a－3)＋9a－3＋6≥12，当且仅当a－3＝9a－3即a＝6时等号成立，这时b＝4，从而所求直线方程为x6＋y4＝1，即2x＋3y－12＝0.1．求直线方程时要注意判断直线斜率是否存在；每条直线都有倾斜角，但不一定每条直线都存在斜率．2．根据斜率求倾斜角，一是要注意倾斜角的范围；二是要考虑正切函数的单调性．3．利用一般式方程Ax＋By＋C＝0求它的方向向量为(－B，A)不可记错，但同时注意方向向量是不唯一的．失误与防范方法与技巧1．要正确理解倾斜角的定义，明确倾斜角的取值范围，熟记斜率公式：k＝y2－y1x2－x1，该公式与两点顺序无关，已知两点坐标(x1≠x2)时，根据该公式可求出经过两点的直线的斜率．当x1＝x2，y1≠y2时，直线的斜率不存在，此时直线的倾斜角为90°.2．求斜率可用k＝tanα(α≠90°)，其中α为倾斜角，由此可见倾斜角与斜率相互联系不可分割，牢记：“斜率变化分两段，90°是分界，遇到斜率要谨记，存在与否需讨论”．3．求直线方程中一种重要的方法就是先设直线方程，再求直线方程中的系数，这种方法叫待定系数法．小结：作业：学案上课后巩固作业谢谢！规范解答解(1)当k＝0时，此时A点与D点重合，折痕所在的直线方程为y＝12.[2分](2)当k≠0时，将矩形折叠后A点落在线段CD上的点为G(a,1)，[4分]所以A与G关于折痕所在的直线对称，有kAG·k＝－1，1ak＝－1⇒a＝－k.[6分]故G点坐标为G(－k,1)，从而折痕所在的直线与AG的交点坐标(线段AG的中点)为M－k2，12.[8分]折痕所在的直线方程为y－12＝kx＋k2，即y＝kx＋k22＋12.[10分]∴k＝0时，y＝12；k≠0时，y＝kx＋k22＋12.[12分]试题：(12分)在平面直角坐标系中，已知矩形ABCD，AB＝2，BC＝1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合．将矩形折叠，使A点落在线DC上．若折痕所在直线的斜率为k，试写出折痕所在直线的方程．审题视角(1)题目已告诉直线斜率为k，即斜率存在．(2)从题意上看，斜率k可以为0，也可以不为0，所以要分类讨论．思想与方法13．求直线方程时，要根据斜率存在与否进行分类讨论批阅笔记(1)求直线方程时，要考虑对斜率是否存在、截距相等时是否为零以及相关位置关系进行分类讨论．(2)本题是对斜率k为0和不为0进行分类讨论．易错点是忽略k＝0的情况．