七年级数学人教版下册期末总复习学案

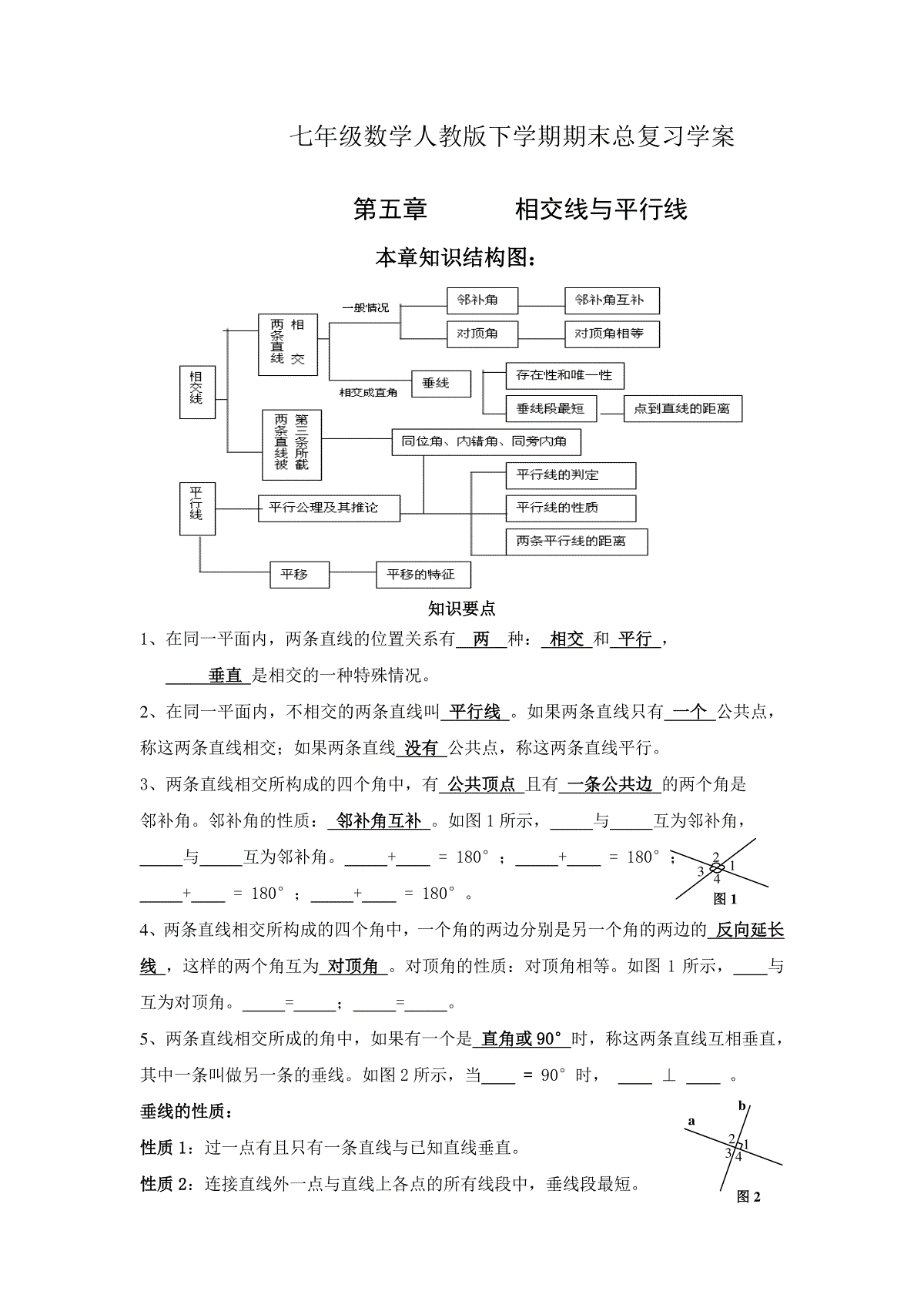
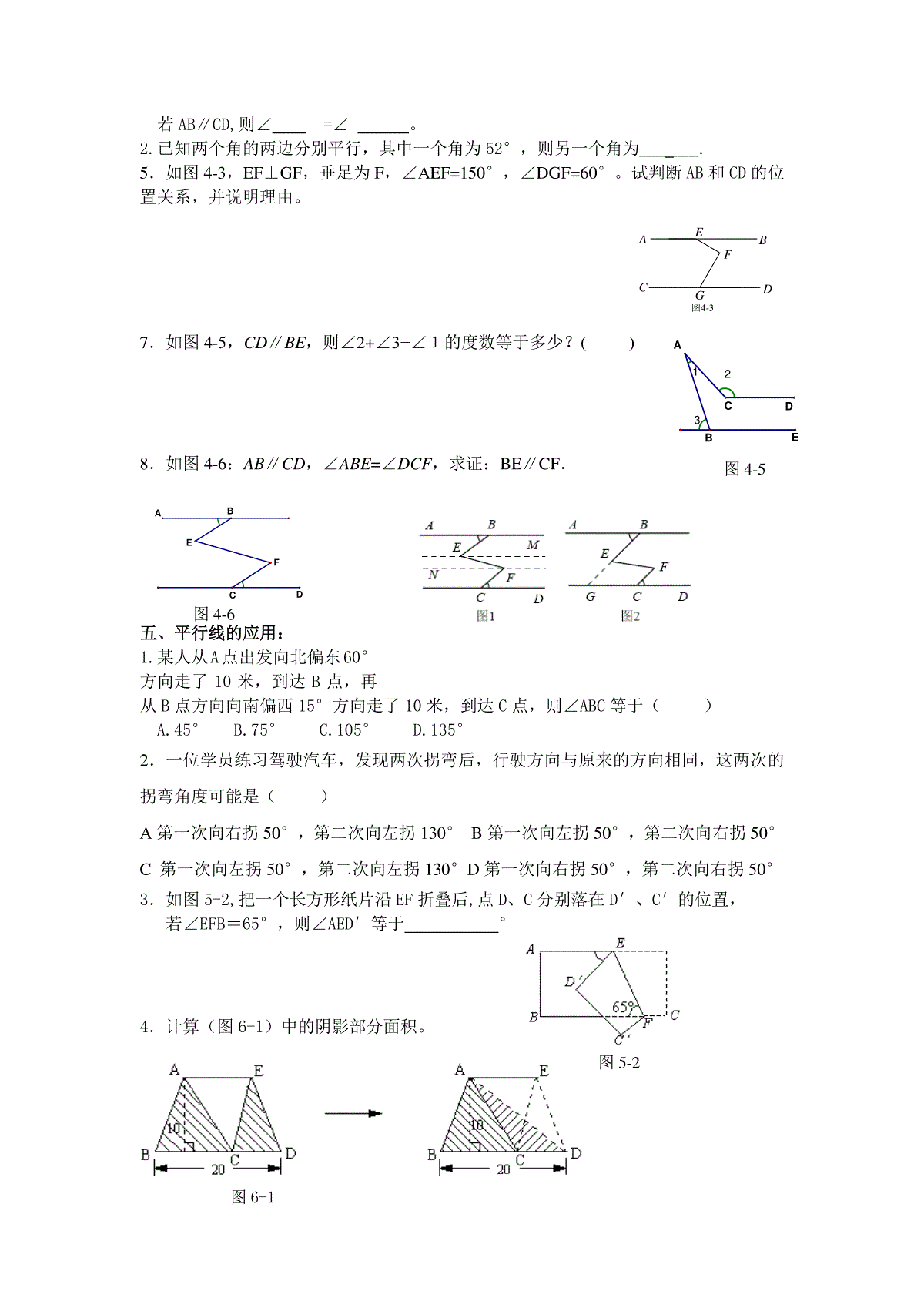
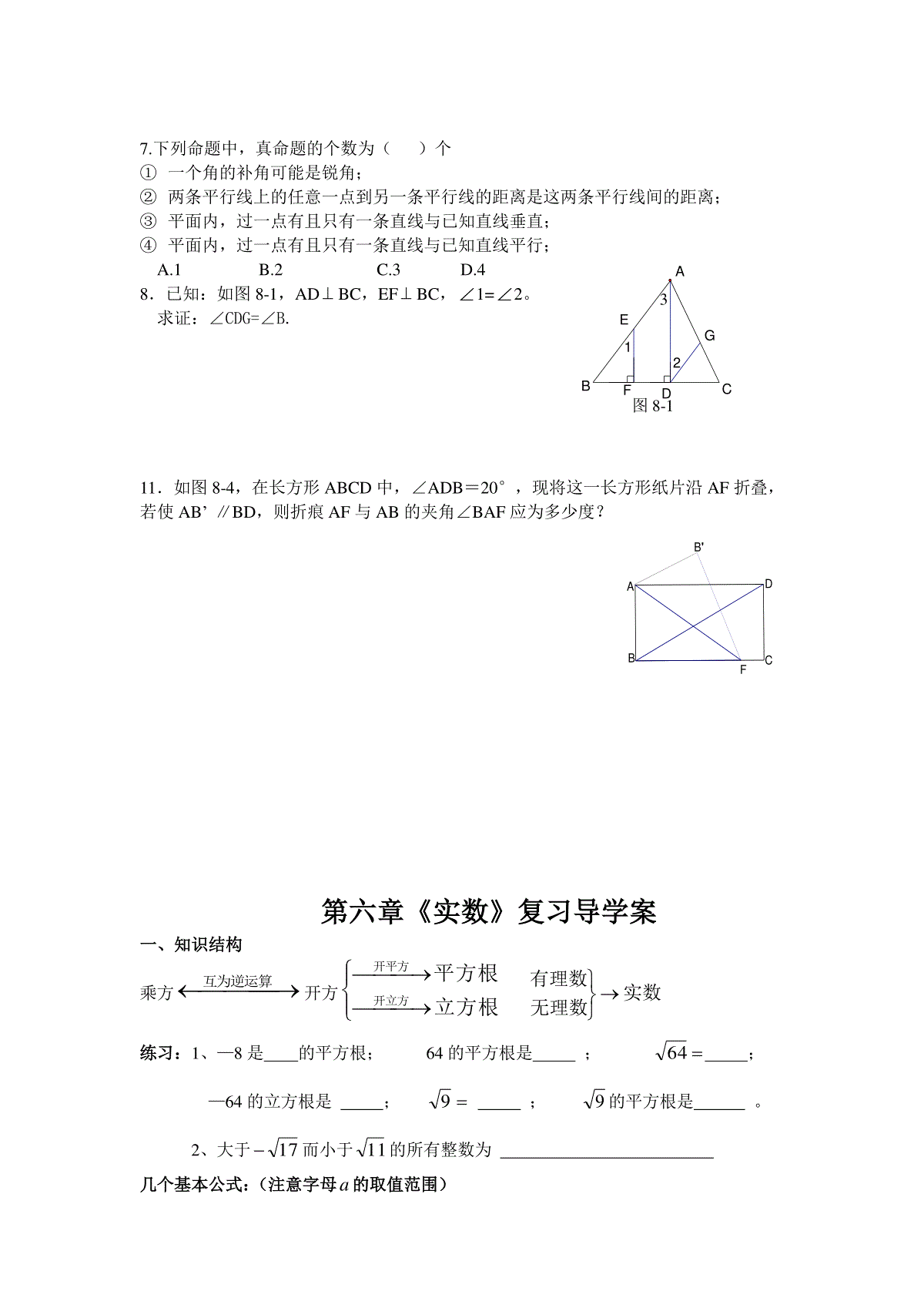
七年级数学人教版下学期期末总复习学案第五章相交线与平行线本章知识结构图：知识要点1、在同一平面内，两条直线的位置关系有两种：相交和平行，垂直是相交的一种特殊情况。2、在同一平面内，不相交的两条直线叫平行线。如果两条直线只有一个公共点，称这两条直线相交；如果两条直线没有公共点，称这两条直线平行。3、两条直线相交所构成的四个角中，有公共顶点且有一条公共边的两个角是邻补角。邻补角的性质：邻补角互补。如图1所示，与互为邻补角，与互为邻补角。+=180°；+=180°；+=180°；+=180°。4、两条直线相交所构成的四个角中，一个角的两边分别是另一个角的两边的反向延长线，这样的两个角互为对顶角。对顶角的性质：对顶角相等。如图1所示，与互为对顶角。=；=。5、两条直线相交所成的角中，如果有一个是直角或90°时，称这两条直线互相垂直，其中一条叫做另一条的垂线。如图2所示，当=90°时，⊥。垂线的性质：性质1：过一点有且只有一条直线与已知直线垂直。性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短。图11342图21342ab性质3：如图2所示，当a⊥b时，====90°。点到直线的距离：直线外一点到这条直线的垂线段的长度叫点到直线的距离。6、同位角、内错角、同旁内角基本特征：①在两条直线(被截线)的同一方，都在第三条直线(截线)的同一侧，这样的两个角叫同位角。图3中，共有对同位角：与是同位角；与是同位角；与是同位角；与是同位角。②在两条直线(被截线)之间，并且在第三条直线(截线)的两侧，这样的两个角叫内错角。图3中，共有对内错角：与是内错角；与是内错角。③在两条直线(被截线)的之间，都在第三条直线(截线)的同一旁，这样的两个角叫同旁内角。图3中，共有对同旁内角：与是同旁内角；与是同旁内角。7、平行公理：经过直线外一点有且只有一条直线与已知直线平行。平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。平行线的性质：性质1：两直线平行，同位角相等。如图4所示，如果a∥b，则=；=；=；=。性质2：两直线平行，内错角相等。如图4所示，如果a∥b，则=；=。性质3：两直线平行，同旁内角互补。如图4所示，如果a∥b，则+=180°；+=180°。性质4：平行于同一条直线的两条直线互相平行。如果a∥b，a∥c，则∥。8、平行线的判定：判定1：同位角相等，两直线平行。如图5所示，如果=或=或=或=，则a∥b。判定2：内错角相等，两直线平行。如图5所示，如果=或=，则a∥b。判定3：同旁内角互补，两直线平行。如图5所示，如果+=180°；+=180°，则a∥b。判定4：平行于同一条直线的两条直线互相平行。如果a∥b，a∥c，则∥。9、判断一件事情的语句叫命题。命题由题设和结论两部分组成，有真命题和假图3a57861342bc图4a57861342bc图5a57861342bc4321图4-1DCBA命题之分。如果题设成立，那么结论一定成立，这样的命题叫真命题；如果题设成立，那么结论不一定成立，这样的命题叫假命题。真命题的正确性是经过推理证实的，这样的真命题叫定理，它可以作为继续推理的依据。10、平移：在平面内，将一个图形沿某个方向移动一定的距离，图形的这种移动叫做平移变换，简称平移。平移后，新图形与原图形的形状和大小完全相同。平移后得到的新图形中每一点，都是由原图形中的某一点移动后得到的，这样的两个点叫做对应点。平移性质：平移前后两个图形中①对应点的连线平行且相等；②对应线段相等；③对应角相等。例题与习题:一、对顶角和邻补角：1.如图所示,∠1和∠2是对顶角的图形有()A.1个B.2个C.3个D.4个2．如图1-1，直线AB、CD、EF都经过点O，图中有几对对顶角。（）3．如图1-2，若∠AOB与∠BOC是一对邻补角，OD平分∠AOB，OE在∠BOC内部，并且∠BOE=12∠COE，∠DOE=72°。求∠COE的度数。（）DBEACO三、同位角、内错角和同旁内角的判断1．如图3-1，按各角的位置，下列判断错误的是（）（A）∠1与∠2是同旁内角（B）∠3与∠4是内错角（C）∠5与∠6是同旁内角（D）∠5与∠8是同位角四、平行线的判定和性质：1.如图4-1，若∠3=∠4，则∥；12121221（图1-2）12345678图3-1图1-1321EACBD若AB∥CD,则∠=∠。2.已知两个角的两边分别平行，其中一个角为52°，则另一个角为_______.5．如图4-3，EF⊥GF，垂足为F，∠AEF=150°，∠DGF=60°。试判断AB和CD的位置关系，并说明理由。GFEDCBA图4-37．如图4-5，CD∥BE，则∠2+∠3−∠１的度数等于多少？()8．如图4-6：AB∥CD，∠ABE=∠DCF，求证：BE∥CF．五、平行线的应用：1.某人从A点出发向北偏东60°方向走了10米，到达B点，再从B点方向向南偏西15°方向走了10米，到达C点，则∠ABC等于（）A.45°B.75°C.105°D.135°2．一位学员练习驾驶汽车，发现两次拐弯后，行驶方向与原来的方向相同，这两次的拐弯角度可能是（）A第一次向右拐50°，第二次向左拐130°B第一次向左拐50°，第二次向右拐50°C第一次向左拐50°，第二次向左拐130°D第一次向右拐50°，第二次向右拐50°3．如图5-2,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置，若∠EFB＝65°，则∠AED′等于°4．计算（图6-1）中的阴影部分面积。DBECFA图4-6图6-1图4-5图5-27.下列命题中，真命题的个数为（）个①一个角的补角可能是锐角；②两条平行线上的任意一点到另一条平行线的距离是这两条平行线间的距离；③平面内，过一点有且只有一条直线与已知直线垂直；④平面内，过一点有且只有一条直线与已知直线平行；A.1B.2C.3D.48．已知：如图8-1，ADBC，EFBC，1=2。求证：∠CDG=∠B.11．如图8-4，在长方形ABCD中，∠ADB＝20°，现将这一长方形纸片沿AF折叠，若使AB’∥BD，则折痕AF与AB的夹角∠BAF应为多少度？B'DFCBA第六章《实数》复习导学案一、知识结构乘方互为逆运算开方立方根平方根开立方开平方实数无理数有理数练习：1、—8是的平方根；64的平方根是；64；—64的立方根是；9；9的平方根是。2、大于17而小于11的所有整数为几个基本公式：（注意字母a的取值范围）E21GFDCBA3图8-12)(a=；2a=33a=；33)(a=；3a=练习：1、判断下列说法是否正确：1.实数不是有理数就是无理数。（）2.无限小数都是无理数。（）3.无理数都是无限小数。（）4.带根号的数都是无理数。（）5.两个无理数之和一定是无理数。（）6.所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。（）7.平面直角坐标系中的点与有序实数对之间是一一对应的。（）2、把下列各数中，有理数为；无理数为3737737773.085094320225233、、、、、、、、、(相邻两个3之间的7逐渐加1个)2、（1）4)3(92y（2）01253273x（3）3232223四、知识提高1、已知732.13，477.530，（1）300；（2）3.0；（3）0.03的平方根约为；（4）若77.54x，则x练习：已知442.133，107.3303，694.63003，求（1）33.0；（2）3000的立方根约为；（3）07.313x，则x2、若xx222，则x的取值范围是4、已知115的小数部分为m，115的小数部分为n，则nm五、当堂反馈1、下列说法正确的是()A、16的平方根是4B、6表示6的算术平方根的相反数C、任何数都有平方根D、2a一定没有平方根2、若335m，则m5、已知等腰三角形的两边长ba,满足013325322baba，求三角形的周长6、如果一个数的平方根是1a和72a，求这个数第七章平面直角坐标系本章知识结构图：知识要点1、有序数对：有顺序的两个数a与b组成的数对叫做有序数对，记做（a,b）。2、平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成平面直角坐标系。3、横轴、纵轴、原点：水平的数轴称为x轴或横轴；竖直的数轴称为y轴或纵轴；两坐标轴的交点为平面直角坐标系的原点。4、坐标：对于平面内任一点P，过P分别向x轴，y轴作垂线，垂足分别在x轴，y轴上，对应的数a,b分别叫点P的横坐标和纵坐标，记作P(a，b)。5、象限：两条坐标轴把平面分成四个部分，右上部分叫第一象限，按逆时针方向依次叫第二象限、第三象限、第四象限。坐标轴上的点不在任何一个象限内。6、各象限点的坐标特点①第一象限的点：横坐标0，纵坐标0；②第二象限的点：横坐标0，纵坐标0；③第三象限的点：横坐标0，纵坐标0；④第四象限的点：横坐标0，纵坐标0。7、坐标轴上点的坐标特点①x轴正半轴上的点：横坐标0，纵坐标0；②x轴负半轴上的点：横坐标0，纵坐标0；③y轴正半轴上的点：横坐标0，纵坐标0；④y轴负半轴上的点：横坐标0，纵坐标0；⑤坐标原点：横坐标0，纵坐标0。(填“”、“”或“=”)8、点P(a，b)到x轴的距离是|b|，到y轴的距离是|a|。9、对称点的坐标特点①关于x轴对称的两个点，横坐标相等，纵坐标互为相反数；②关于y轴对称的两个点，纵坐标相等，横坐标互为相反数；③关于原点对称的两个点，横坐标、纵坐标分别互为相反数。10、点P(2，3)到x轴的距离是；到y轴的距离是；点P(2，3)关于x轴对称的点坐标为(，)；点P(2，3)关于y轴对称的点坐标为(，)。11、如果两个点的横坐标相同，则过这两点的直线与y轴平行、与x轴垂直；如果两点的纵坐标相同，则过这两点的直线与x轴平行、与y轴垂直。如果点P(2，3)、Q(2，6)，这两点横坐标相同，则PQ∥y轴，PQ⊥x轴；如果点P(-1，2)、Q(4，2)，这两点纵坐标相同，则PQ∥x轴，PQ⊥y轴。12、平行于x轴的直线上的点的纵坐标相同；平行于y轴的直线上的点的横坐标相同；在一、三象限角平分线上的点的横坐标与纵坐标相同；在二、四象限角平分线上的点的横坐标与纵坐标互为相反数。如果点P(a，b)在一、三象限角平分线上，则P点的横坐标与纵坐标相同，即a=b；如果点P(a，b)在二、四象限角平分线上，则P点的横坐标与纵坐标互为相反数，即a=－b。13、表示一个点(或物体)的位置的方法：一是准确恰当地建立平面直角坐标系；二是正确写出物体或某地所在的点的坐标。选择的坐标原点不同，建立的平面直角坐标系也不同，得到的同一个点的坐标也不同。14、图形的平移可以转化为点的平移。坐标平移规律：①左右平移时，横坐标进行加减，纵坐标不变；②上下平移时，横坐标不变，纵坐标进行加减；③坐标进行加减时，按“左减右加、上加下减”的规律进行。如将点P(2，3)向左平移2个单位后得到的点的坐标为(，)；将点P(2，3)向右平移2个单位后得到的点的坐标为(，)；将点P(2，3)向上平移2个单位后得到的点的坐标为(，)；将点P(2，3)向下平移2个单位后得到的点的坐标为(，)；将点P(2，3)先向左平移3个单位后再向上平移5个单位后得到的点的坐标为(，)；将点P(2，3)先向左平移3个单位后再向下平移5个单位后得到的点的坐标为(，)；将点P(2，3)先向右平移3个单位后再向上平移5个单位后得到的点的坐标为(，)；将点P(2，3)先向右平移3个单位后再向下平移5个单位后得到的点的坐标为(，)。例题与习题：一、填空：1．已知点P(3a-8，a-1).(1)点P在x轴上，则P点坐标为；(2)点P在第二象限，并且a为整数，则P点坐标为；(3)Q点坐标为（3，-6），并且直线PQ∥x轴，则P点坐标为.2．如图的棋盘中，若“帅”位于点（1，－2）上，“相”位于点（3